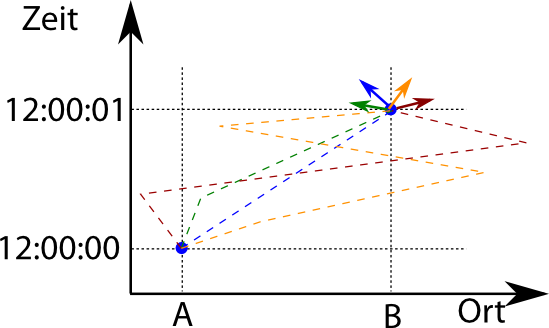
Das tut ihr jetzt für jeden der möglichen Pfade von A nach B. Am Ende habt ihr dann also jeden denkbaren Pfad von A nach B genommen und zu jedem gehört ein Pfeil, der in eine Richtung zeigt (statt unendlicher vieler Pfade zeichne ich nur vier):
Jetzt hängt ihr alle diese Pfeile hintereinander, also immer den Startpunkt des einen Pfeils hinter den Endpunkt des vorigen Pfeils. (Weil das unendlich viele Pfeile sind, ist diese Operation mathematisch etwas trickreich, aber das muss euch nicht stören, weil es hier nur um die Anschauung geht.) Das gibt dann einen Gesamtpfeil (in schwarz):
Als nächstes zeichnet ihr ein Quadrat, dessen Kantenlänge gleich der Länge des Gesamtpfeils ist:
Und jetzt kommt der Trick des Ganzen: Die Fläche dieses Quadrats gibt euch die Wahrscheinlichkeit dafür, dass das Teilchen von A nach B fliegt. Das ist alles. (Diese ganze Erklärung mit den Pfeilen stammt übrigens von Feynman aus dem Buch “QED – the strange theory of light and matter”.)
Auch wenn die Prozedur auf den ersten Blick etwas kompliziert aussieht, ist sie konzeptionell doch sehr einfach: Ihr betrachtet alle Möglichkeiten, wie das Teilchen von A nach B kommen kann. Jeder dieser Möglichkeiten ordnet ihr einen Pfeil zu, dessen Drehwinkel durch die Wirkung auf diesem Weg gegeben ist. Alle diese Pfeile hängt ihr hintereinander und bekommt direkt die Wahrscheinlichkeit dafür, dass der Prozess stattfindet.
Pfadintegrale und die klassische Physik
Auch bei den Pfadintegralen kann man wieder die Verbindung zur klassischen Physik herstellen – dort war es ja so, dass sich das teilchen auf dem Weg mit der kleinsten Wirkung bewegt – das ist also der, bei dem sich der Pfeil am wenigsten gedreht hat. In der QM sollte also dieser Weg zum Endergebnis am stärksten beitragen, wenn es sich um ein Teilchen handel,t das man mit den Mittel der klassischen Physik beschreiben kann.
So ist es auch tatsächlich: Für ein solches Teilchen ist die Wirkung ja viel viel größer als das Plancksche Wirkungsquantum h. Das bedeutet, dass die Drehgeschwindigkeit des Pfeils sehr groß ist – der Pfeil dreht sich also auf jedem Weg von A nach B sehr sehr oft herum, bis er in seiner Endstellung ankommt.
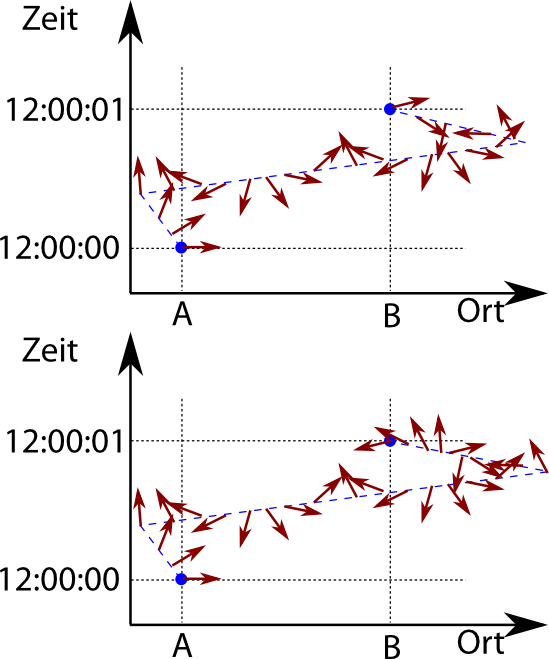
Betrachten wir jetzt einen beliebigen Weg von A nach B (nicht den mit der kleinsten Wirkung, sondern einen anderen). Wenn sich der Pfeil extrem schnell dreht, dann muss ich diesen Weg nur ein klein wenig verändern (im zweiten Bild habe ich ihn rechts ein Stückchen länger gemacht, das lässt sich am schnellsten zeichnen), und ich bekomme einen Weg, bei dem der Pfeil genau in die entgegengesetzte Richtung zeigt:
Die Pfeile dieser beiden Wege tragen also zum Endergebnis nichts bei, weil sie sich gegenseitig aufheben.
Hmm – aber gilt das dann nicht für alle Wege? Dann heben sich alle Pfeile immer gegenseitig weg und die Wahrscheinlichkeit ist immer null, weil alle Pfeile sich aufheben. Teilchen können sich also nie von A nach B bewegen (egal wo A oder B ist) – das scheint nicht so ganz korrekt zu sein, oder?
Ist es auch nicht – es gibt nämlich einen Weg, bei dem das Argument nicht gilt: Den Weg mit der kleinsten Wirkung. Betrachtet diesen Weg, zu dem ein entsprechender Pfeil gehört. Als nächstes betrachten wir zwei Wege, die zu diesem fast identisch sind – damit ist ihre Wirkung auch fast identisch (mathematisch liegt das daran, dass wir das Minimum der Wirkung betrachten, und in der Nähe des Minimums verschwindet ja die erste Ableitung). Die Pfeile dieser Wege zeigen also fast in dieselbe Richtung. Hier einer der beiden Pfade; weil er etwas länger ist, rotiert der Pfeil ein klein wenig weiter, aber nicht sehr viel (ich zeichne nur einen, sonst wird’s unübersichtlich, und ich bin mit den Farben der Pfeile nicht ganz konsequent gewesen, ich hoffe das verwirrt nicht…):









Kommentare (43)