Der Pfeil dieses Pfades und der des Weges mit kleinster Wirkung heben sich also nicht weg, sondern verstärken sich. Deswegen wird in diesem Fall die Wahrscheinlichkeit vom Pfad mit der kleinsten Wirkung dominiert.
Weichen wir stärker vom Weg minimaler Wirkung ab, dann finden wir natürlich auch einen Weg, dessen Pfeil dem des Weges mit der kleinsten Wirkung entgegengesetzt ist, aber zu diesem Weg finden wir dann wieder einen, der dessen Pfeil kompensiert. Insgesamt ergibt sich also ein großer Beitrag von solchen Wegen, bei denen die Wirkung (fast) minimal ist und damit wieder genau das Bild der klassischen Physik. Ausführlich habe ich das übrigens auch in meiner QFT-Serie diskutiert.
Energie- und Impulserhaltung
Die Darstellung mit Pfadintegralen (und später dann die mit Feynman-Diagrammen) führt immer wieder zu Verwirrung, weil die einzelnen Pfade, die wir hier betrachten, ja ziemlich seltsam sind: Das Teilchen fliegt einfach so im Zickzack und ändert dabei seine Geschwindigkeit. Was ist denn mit der Energie- und der Impulserhaltung? Gelten die in der QM nicht mehr? (Das glauben viele Leute, weil es ja auch die Unschärferelation gibt – wenn man den Impuls nicht genau bestimmen kann, dann kann er ja wohl auch nicht exakt erhalten sein, oder?) Um das zu verstehen, muss man etwas genauer hinschauen.
Warnung: Das was ich jetzt schreibe, habe ich in genau dieser Form in keinem Physikbuch diskutiert gefunden; es gibt ein paar Diskussionen beim Physikforum, in denen diese Problematik besprochen wird und ich bin mir ziemlich sicher, dass es stimmt, aber bevor ihr es in eurer Masterprüfung so wiedergebt, solltet ihr vielleicht nochmal die Prüferin fragen. Ich bin mir auch nicht ganz sicher, ob das, was ich hier schreibe, wirklich verständlich (oder gar allgemeinverständlich) ist – beschwert euch im Zweifel in den Kommentaren.
Im folgenden betrachte ich nur die Impulserhaltung; für die Energieerhaltung geht das Argument letztlich genauso (und in der QFT sorgt die Relativitätstheorie dafür, dass Energie und Impuls nur zwei Aspekte derselben Sache sind).
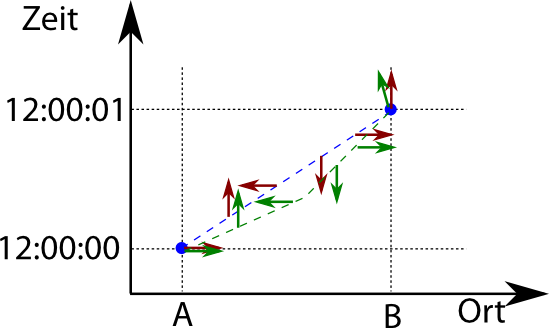
Wir haben also um 12:00:00 unser Teilchen bei A gemessen. Betrachten wir einen der möglichen Pfade von A nach B, und zwar einen Zickzackpfad. Wenn das Teilchen diesen Pfad nimmt, dann ist während des Wegs von A nach B der Impuls nicht erhalten, weil das Teilchen ja seine Geschwindigkeit abrupt ändert. Trotzdem trägt dieser Pfad zur Gesamtwahrscheinlichkeit bei. Solange wir allerdings nur den Ort des Teilchens bei A und B messen, wissen wir über seinen Impuls vorher und hinterher nichts, insofern können wir kein direktes Problem mit der Impulserhaltung feststellen, weil wir den Impuls ja nicht kennen.
Probieren wir also etwas anderes: Wir geben dem Teilchen am Anfang (bei 12:00:00Uhr) einen genau bekannten Wert des Impulses. Damit ist sein Aufenthaltsort allerdings – wegen der Unschärfe – vollkommen unbestimmt. Messen wir den Impuls des Teilchens um 12:00:01 erneut, so messen wir exakt denselben Wert, die Impulserhaltung ist gewährleistet. Das liegt daran, dass die Aufenthaltswahrscheinlichkeit sich zeitlich nicht ändert (wer’s gern mathematisch ausdrückt: Der Impulseigenzustand ist auch ein Energieeigenzustand und deshalb bis auf einen Phasenfaktor zeitlich konstant.)
Wie beschreiben wir den Zustand mit festem Impuls im Pfadintegral-Bild? Das ist auf den ersten Blick nicht so einfach, denn wir sind ja immer an einem Ort (A) losgelaufen und an einem anderen Ort (B) geendet – jetzt aber wissen wir den Ort nicht, sondern kennen nur den Impuls am Anfang und am Ende. Wir können aber nach den Regeln der QM den Zustand mit festem Impuls am Anfang als eine Überlagerung aus lauter Zuständen ansehen, bei denen das Teilchen an einem bestimmten Ort ist. (Das mit den Überlagerungen habe ich in meiner QM-Serie ausführlicher erklärt.)
Wir betrachten also den Zustand unseres Teilchens mit festem Impuls zur Zeit 12:00:00 als eine Überlagerung aus Zuständen, an denen das Teilchen an jeweils einem Ort ist. Genauso betrachten wir den Zustand zur Zeit 12:00:01 mit festem Impuls ebenfalls als eine Überlagerung aus allen denkbaren Ortszuständen. Die Gesamtwahrscheinlichkeit, dass ein teilchen mit einem bestimmten Impuls zur Zeit 12.00:00 zu einem teilchen mit einem bestimmten Impuls zur zeit 12.00:01 wird, ergibt sich jetzt als Überlagerung aller Möglichkeiten, von jedem der denkbaren Startpunkte zu jedem der denkbaren Endpunkte zu kommen. Eine dieser Möglichkeiten ist unser alter Bekannter: Der Weg von A nach B. Die Wahrscheinlichkeit für diesen Weg wiederum können wir berechnen, indem wir alle denkbaren Möglichkeite, von A nach B zu kommen, aufaddieren, so wie wir es oben gemacht haben. Das gleiche müssen wir aber auch für alle anderen denkbaren Kombinationen von Start- und Zielpunkt tun, weil ja alle möglichen Start- und Zielpunkte beitragen.






Kommentare (43)