In dieser kleinen Artikelserie passiert wirklich nichts Aufregendes – ein Teilchen fliegt von A nach B. Aber je tiefer man in die Physik einsteigt, desto komplexer wird dieser unglaublich einfache Prozess: In der klassischen Physik fliegt das Teilchen einfach von A nach B, in der Quantenmechanik haben wir plötzlich (in der üblichen Formulierung) Warhscheinlichkeitsverteilungen, die sich zeitlich entwickeln, und wenn wir das Bild des Pfadintegrals verwenden, dann können wir unser Teilchen so beschreiben, als würde es alle denkbaren Wege mit allen denkbaren Geschwindigkeiten gleichzeitig nehmen und am Ende alle diese Wege miteinander interferieren lassen.
Und als ob das noch nicht genug wäre, geht es noch komplizierter, wenn wir berücksichtigen, dass unser Teilchen auch noch mit anderen Teilchen wechselwirken kann.
Moment – wieso wechselwirken? Sollte unser Teilchen nicht einfach durchs Vakuum fliegen (mal abgesehen von den beiden Detektoren)? Ja, sollte es. Aber das Vakuum ist ja auch nicht mehr das, was es mal war, sondern ein nicht ganz unkompliziertes Gebilde. (Und, ja, ich weiß, dass in meiner Vakuum-Serie auch noch mindestens ein Teil aussteht – hat jemand Lust, mir ne Vollzeitanstellung als Blogger zu finanzieren?) Wenn also ein Teilchen durch die Gegend fliegt, dann kann unterwegs alles mögliche passieren (und alle diese Möglichkeiten müssen wir am Ende, wie beim Pfadintegral in der QM, miteinander interferieren lassen).
Machen wir die Sache etwas konkreter und nehmen als Teilchen, das von A nach B fliegt, ein Elektron. Ich betrachte hier zunächst einmal nur die Theorie der Quantenelektrodynamik; unser Elektron darf also nur mit Photonen, den Teilchen des Lichts, wechselwirken.
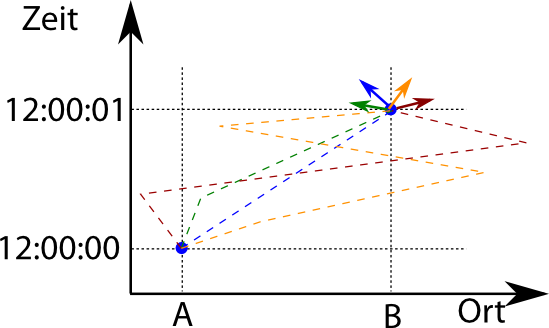
Im letzten Teil haben wir den Weg des Elektrons von A nach B als Überlagerung über alle denkbaren Wege beschrieben, etwa so:
Zu jedem denkbaren Weg gehört dabei ein Pfeil und am Ende muss man alle diese Pfeile hintereinanderhängen, um die Gesamtwahrscheinlichkeit herauszubekommen, dass das teilchen von A nach B fliegt.
Jetzt aber kommt noch hinzu, dass unser Elektron auf jedem dieser Wege auch noch etwas anderes tun kann, als einfach irgendwo herumzufliegen – es kann zum Beispiel ein Photon aussenden:
Geht das wirklich so? Nein, eigentlich nicht. Betrachten wir wieder den Fall, dass unser Elektron am Anfang einen bestimmten Impuls hat. Damit liegt auch seine Bewegungsenergie fest, denn Impuls ist (bei nicht-relativistischen Geschwindigkeiten) Masse mal Geschwindigkeit und die Bewegungsenergie ist ein-halb mal Masse mal Geschwindigkeit ins Quadrat.Wenn unser Elektron jetzt ein Photon mit einer bestimmten Energie aussendet, dann verringert sich die Energie des Elektrons um diesen Betrag und entsprechend verringert sich auch seine Geschwindigkeit und damit sein Impuls. Damit die Impulserhaltung gelten kann, müsste dieser Impuls jetzt auf das Photon übertragen werden. Dummerweise gibt es aber auch für Photonen eine eindeutige Beziehung zwischen Energie und Impuls – und die Formeln passen nicht so zusammen, dass unser Photon sowohl den fehlenden Impuls als auch die fehlende Energie des Elektrons übernehmen könnte. Ein frei herumfliegendes Elektron kann also kein Photon einfach so aussenden, dann könnten wir am Ende den Impuls von Elektron und Photon und deren Energien messen und eine Verletzung der Impuls- oder Energieerhaltung bekommen.
Was es aber tun kann, ist, das Photon erst auszusenden und dann wieder zu absorbieren. (Ihr solltet euch inzwischen nicht mehr darüber wundern, dass ein Photon ausgesandt und wieder eingefangen werden kann – auch für das Photon müssen alle denkbaren Wege berücksichtigt werden, nicht nur die, bei denen es brav mit konstanter Lichtgeschwindigkeit fliegt. Wenn wir Zustände mit festem Impuls betrachten, dann ist der Aufenthaltsort unserer Teilchen eh nicht festgelegt, sondern sie sind über den ganzen Raum “verschmiert”.)
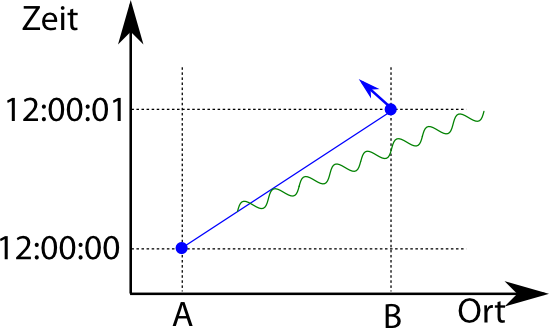
Ich zeichne das mal so, obwohl ich hier jetzt wieder ein Elektron habe, das mit eindeutigem Ort losfliegt (also keinen eindeutigen Impuls hat):






Kommentare (38)