“Wie soll das denn gehen?” fragt ihr euch jetzt vielleicht. Zwischendrin hat doch das Elektron ein Photon ausgesendet und damit haben wir doch ein Problem mit der Energie- und Impulserhaltung, oder nicht? Nein, überraschenderweise haben wir das nicht, aber die Physik ist hier trotzdem seltsam. Nachdem das Elektron das Photon ausgesandt hat, hat es seine Energie und seinen Impuls geändert und das Photon trägt genau diese Energie und diesen Impuls weg (bringt beide aber bei der Absorption brav wieder zurück). Die Energie- und Impulserhaltung ist also gewährleistet.
“Moment, du hast doch gerade erklärt, dass das nicht geht, weil die Energie-Impuls-Beziehungen nicht passen!” beschwert ihr euch als nächstes, richtig? Recht habt ihr – aber unser Elektron und unser Photon haben im Moment (also zwischen dem Aussenden und dem Einfangen des Photons) einfach nicht die richtige Beziehung zwischen Energie und Impuls. Das Elektron kann zum Beispiel einen riesigen Impuls und eine sehr kleine kinetische Energie haben (oder umgekehrt). Solche Teilchen, bei denen die Energie-Impuls-Beziehung nicht passt, nennt man virtuelle Teilchen, dazu habe ich letztes Jahr schon etwas geschrieben.
Allerdings ist wieder mal Vorsicht geboten: Wir haben hier einen einzigen Prozess betrachtet, bei dem das Elektron ein Photon aussendet. tatsächlich muss man aber wieder einmal alle Möglichkeiten berücksichtigen, wie das Elektron ein (oder auch mehrere) Photonen aussenden und wieder einfangen kann.
Diagramme dieser Art nennt man übrigens auch Feynman-Diagramme.
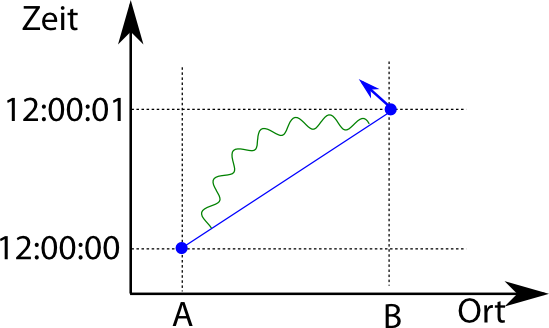
Anmerkung für PhysikerInnen: Man kann Feynman-Diagramme im Orts- oder im Impulsraum lesen. Normalerweise bezeichnet man die Achsen im Diagramm ja einmal als Orts- und einmal als Zeit-Achse. Die Vertices, wo Teilchen absorbiert oder emittiert werden, liegen dann an einem bestimmten Ort. Um alle Möglichkeiten zu berücksichtigen, muss man dann aber über alle denkbaren Orte integrieren. Tut man das für den Fall, wo alle ein- und ausfliegenden Teilchen in Impulseigenzuständen sind, dann sorgt die Integration über den Ort gerade dafür, dass man die Fouriertransformierte der Delta-Distribution für den Impuls bekommt. Mit anderen Worten: Die Integration über den Ort (und die Zeit) sorgt genau für die Erhaltung des Impulses (und der Energie) an jedem Vertex. Die Rechnung dazu steht vermutlich in jedem QFT-Buch der Welt, nicht alle machen sich aber die Mühe, die doppelte Interpretation von Feynmandiagrammen (lesbar im Orts- oder im Impulsraum) explizit zu erwähnen, was zumindest bei mir immer zu massiver Verwirrung geführt hat. (Ende der Anmerkung)
Wir müssen für unser Elektron auf seinem Weg von A nach B nicht nur alle denkbaren Wege überlagern, sondern auch noch alle Möglichkeiten, wie das Elektron unterwegs ein (oder auch mehrere) Photonen aussenden kann, wobei dann zwischendurch aus dem Elektron ein “virtuelles” Elektron wird, bei dem die Energie-Impuls-Beziehung nicht passt. Solche Teilchen nennt man auch Teilchen, die “nicht auf der Massenschale liegen” oder kurz “off-shell”-Teilchen. (Der Begriff “Massenschale” stammt aus der Relativitätstheorie und drückt gerade die Verknüpfung zwischen Energie und Impuls aus. Das erkläre ich jetzt aber nicht auch noch (hätte ich klugerweise im ersten Teil machen können, da habe ich aber nicht dran gedacht…))
Unendlichkeiten, Renormierung und all das
“Gut”, sagt ihr vermutlich, “dann rechnen die Physikerinnen diese ganzen Wechselwirkungen eben auch noch mit aus, das wird ja vermutlich auch nicht schlimmer sein, als das, was wir bisher gemacht haben.” Aber leider ist dieser Optimismus nicht wirklich gerechtfertigt.
Wir müssen ja (wie im letzten Teil erklärt) einen Pfeil für jede Möglichkeit berechnen, mit dem wir den Beitrag des einzelnen Pfades bewerten, und am Ende alle diese Pfeile zu einem Gesamtpfeil addieren, aus dem wir dann die Wahrscheinlichkeit des Prozesses berechnen. Rechnet man nun aus, wie schnell sich dieser Pfeil dreht, wenn man den Prozess mit dem ausgesandten und wieder eingefangenen Photon berücksichtigt, dann kommt man auf einen mathematisch eindeutigen, aber physikalisch ziemlich unhandlichen Wert: Unendlich.






Kommentare (38)