Auf seinem Weg von A nach B hat unser Teilchen in den letzten Teilen so einiges erlebt: Es hat den Weg maximaler Eigenzeit und minimaler Wirkung gewählt, es hatte eine zerlaufende Wahrscheinlichkeitsverteilung, es ging irgendwie alle denkbaren Wege gleichzeitig und hat schließlich unterwegs auch noch virtuelle Photonen ausgesandt und wurde mit fiesen Unendlichkeiten konfrontiert. Aber das ist noch nicht alles.
Zunächst einmal kann unser Elektron auch noch andere virtuelle Teilchen aussenden und wieder einfangen. (Wie wir im letzten Teil und auch in diesem Artikel hier gesehen haben, ist der Begriff des “virtuellen Teilchens” nicht ganz unproblematisch. Man sollte sich nicht vorstellen, dass da ständig irgendwelche Teilchen entstehen und wieder vergehen, denn man muss ja alle denkbaren Möglichkeiten überlagern – genau wie bei den unendlich vielen möglichen Wegen von A nach B. Das Bild der virtuellen Teilchen ist praktisch und hilft in vielen Fällen dabei, die Prozesse einfach berechnen zu können, aber es ist letztlich nur eine Modellvorstellung.)
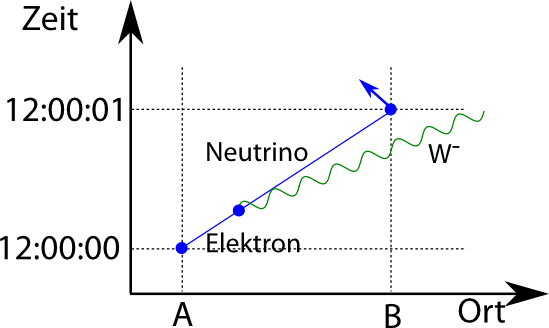
Elektronen sind nicht nur elektrisch geladen, sondern sie unterliegen auch der so genannten schwachen Wechselwirkung, die Teilchen in andere Teilchen umwandeln kann. Ein Elektron kann zum Beispiel ein Teilchen namens W– aussenden und sich dabei in ein Neutrino verwandeln.
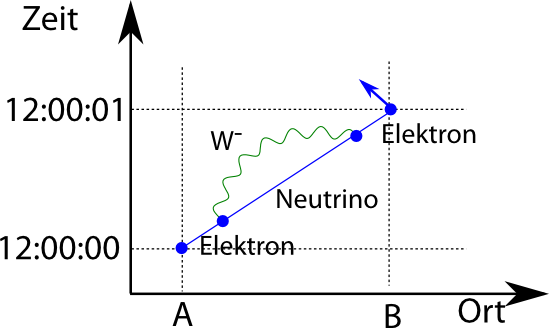
Bei einem freien Elektron klappt das nicht, denn das W– hat eine hohe Masse und wir bekommen Probleme mit der Energieerhaltung. Es spricht aber nichts gegen die Aussendung eines virtuellen W– , das dann wieder eingefangen wird:
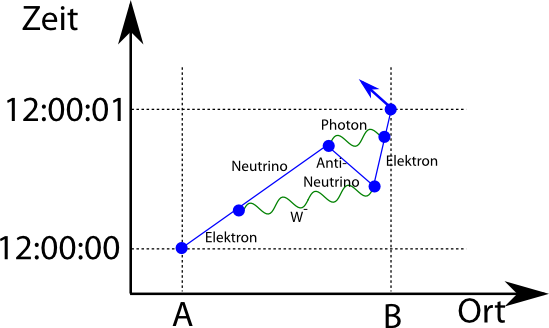
Auch kompliziertere Prozesse sind möglich, beispielsweise kann das W– selbst wieder in ein Elektron und ein Antineutrino zerfallen und das Antineutrino vernichtet dann das ursprüngliche Neutrino, wobei ein Photon entsteht, das dann wieder vom Elektron absorbiert wird (mit kleiner Schrift, sonst sieht man nix…):
Alle diese Prozesse müssen wir theoretisch berücksichtigen, denn sie beeinflussen den Weg unseres Teilchens von A nach B, weil sie als Möglichkeiten beitragen.
Praktisch allerdings brauchen wir uns um diese Prozesse erst einmal gar nicht zu kümmern, denn sie sind schon in dem physikalischen Wert der Masse enthalten, den wir für das Elektron messen. Das war ja gerade der Trick mit der Renormierung, den wir letztes Mal kennengelernt haben. Wäre es anders, dann könte man allein aus der Beobachtung der Masse unterschiedlicher Teilchen schon Rückschlüsse ziehen, welche Wechselwirkungen es in der Natur gibt – das funktioniert aber nicht, weil wir eben nie ein “nacktes” Elektron ohne all seine Wechselwirkungen beobachten können.
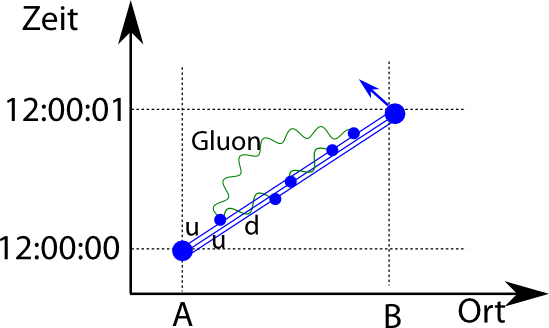
Neben der schwachen Wechselwirkung gibt es auch noch die starke Wechselwirkung, für die Elektronen unempfänglich sind, die aber auf Quarks wirkt. Wenn unser Teilchen, das von A nach B fliegt, also ein Proton ist, dann müssen wir auch solche Prozesse berücksichtigen, bei denen Gluonen ausgesandt werden, die Teilchen der starken Wechselwirkung. Das Proton besteht aus drei Quarks, kurz u, u und d genannt:
Weil das Proton aus mehreren Quarks besteht, werden zwischen diesen – in dieser Modellvorstellung – ständig virtuelle Gluonen ausgetauscht:
Prinzipiell scheint das nicht viel neues zu bringen, aber es gibt hier eine zusätzliche Komplikation: Bei Elektronen, die virtuelle Photonen aussenden, tragen sehr komplizierte Feynman-Diagramme mit vielen virtuellen Photonen nur wenig zum Gesamtergebnis bei. Das liegt daran, dass die elektrische Wechselwirkung vergleichsweise schwach ist – je mehr Photonen ausgesandt und eingefangen werden, desto unwahrscheinlicher ist der jeweilige Prozess. Bei der starken Wechselwirkung ist das anders – die ist so stark, dass man nicht unbedingt annehmen kann, dass Prozesse mit 110 Gluonen unwahrscheinlicher sind als solche mit einem. Ich erwähne das hier nur, weil es wieder einmal zeigt, dass die Vorstellung mit den virtuellen Teilchen nicht unproblematisch ist.
Eine andere Darstellung der Masse
Insgesamt beschreiben wir unser Teilchen auf dem Weg von A nach B aber mit einer Formel, in der die (renormierte, also letztlich die experimentell gemessene) Masse drin steckt. Hätte es eine andere Masse, dann hätte es natürlich auch eine andere kinetische Energie; hätte es gar keine Masse, dann würde es sich mit Lichtgeschwindigkeit bewegen, jedenfalls, nachdem man über alle Möglichkeiten für den Weg von A nach B summiert hat. Die Masse bestimmt also, wie sich ein Teilchen von A nach B bewegt, und für jedes Wegstückchen, bei dem sich unser Teilchen auf einem geraden Weg mit konstanter Geschwindigkeit bewegt hat, konnten wir einfach diese Formel verwenden, um den Beitrag zur Gesamt-Wahrscheinlichkeit zu bestimmen.







Kommentare (75)