Auf seinem Weg von A nach B hat unser Teilchen in den letzten Teilen so einiges erlebt: Es hat den Weg maximaler Eigenzeit und minimaler Wirkung gewählt, es hatte eine zerlaufende Wahrscheinlichkeitsverteilung, es ging irgendwie alle denkbaren Wege gleichzeitig und hat schließlich unterwegs auch noch virtuelle Photonen ausgesandt und wurde mit fiesen Unendlichkeiten konfrontiert. Aber das ist noch nicht alles.
Zunächst einmal kann unser Elektron auch noch andere virtuelle Teilchen aussenden und wieder einfangen. (Wie wir im letzten Teil und auch in diesem Artikel hier gesehen haben, ist der Begriff des “virtuellen Teilchens” nicht ganz unproblematisch. Man sollte sich nicht vorstellen, dass da ständig irgendwelche Teilchen entstehen und wieder vergehen, denn man muss ja alle denkbaren Möglichkeiten überlagern – genau wie bei den unendlich vielen möglichen Wegen von A nach B. Das Bild der virtuellen Teilchen ist praktisch und hilft in vielen Fällen dabei, die Prozesse einfach berechnen zu können, aber es ist letztlich nur eine Modellvorstellung.)
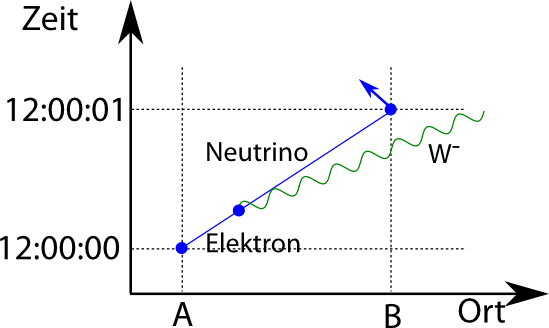
Elektronen sind nicht nur elektrisch geladen, sondern sie unterliegen auch der so genannten schwachen Wechselwirkung, die Teilchen in andere Teilchen umwandeln kann. Ein Elektron kann zum Beispiel ein Teilchen namens W– aussenden und sich dabei in ein Neutrino verwandeln.
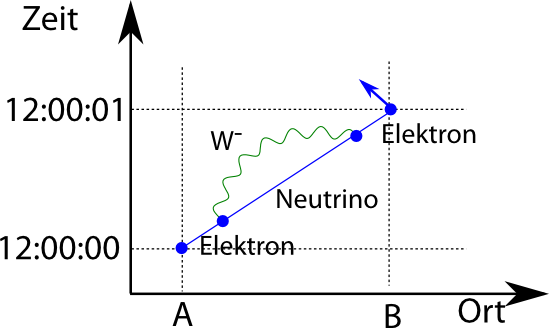
Bei einem freien Elektron klappt das nicht, denn das W– hat eine hohe Masse und wir bekommen Probleme mit der Energieerhaltung. Es spricht aber nichts gegen die Aussendung eines virtuellen W– , das dann wieder eingefangen wird:
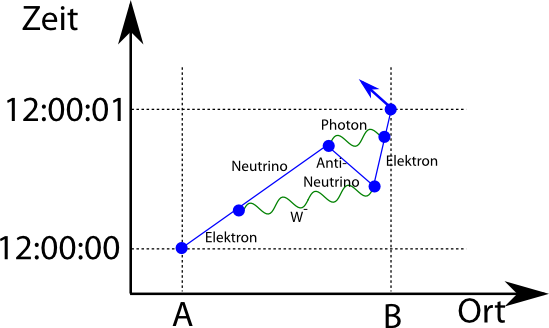
Auch kompliziertere Prozesse sind möglich, beispielsweise kann das W– selbst wieder in ein Elektron und ein Antineutrino zerfallen und das Antineutrino vernichtet dann das ursprüngliche Neutrino, wobei ein Photon entsteht, das dann wieder vom Elektron absorbiert wird (mit kleiner Schrift, sonst sieht man nix…):
Alle diese Prozesse müssen wir theoretisch berücksichtigen, denn sie beeinflussen den Weg unseres Teilchens von A nach B, weil sie als Möglichkeiten beitragen.
Praktisch allerdings brauchen wir uns um diese Prozesse erst einmal gar nicht zu kümmern, denn sie sind schon in dem physikalischen Wert der Masse enthalten, den wir für das Elektron messen. Das war ja gerade der Trick mit der Renormierung, den wir letztes Mal kennengelernt haben. Wäre es anders, dann könte man allein aus der Beobachtung der Masse unterschiedlicher Teilchen schon Rückschlüsse ziehen, welche Wechselwirkungen es in der Natur gibt – das funktioniert aber nicht, weil wir eben nie ein “nacktes” Elektron ohne all seine Wechselwirkungen beobachten können.
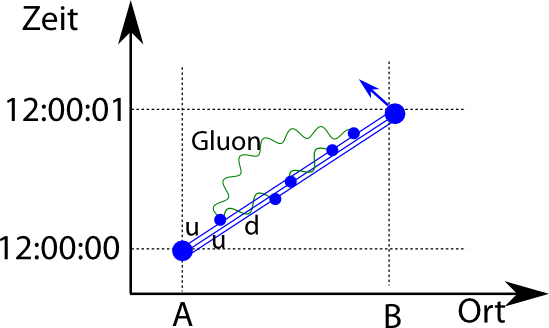
Neben der schwachen Wechselwirkung gibt es auch noch die starke Wechselwirkung, für die Elektronen unempfänglich sind, die aber auf Quarks wirkt. Wenn unser Teilchen, das von A nach B fliegt, also ein Proton ist, dann müssen wir auch solche Prozesse berücksichtigen, bei denen Gluonen ausgesandt werden, die Teilchen der starken Wechselwirkung. Das Proton besteht aus drei Quarks, kurz u, u und d genannt:
Weil das Proton aus mehreren Quarks besteht, werden zwischen diesen – in dieser Modellvorstellung – ständig virtuelle Gluonen ausgetauscht:
Prinzipiell scheint das nicht viel neues zu bringen, aber es gibt hier eine zusätzliche Komplikation: Bei Elektronen, die virtuelle Photonen aussenden, tragen sehr komplizierte Feynman-Diagramme mit vielen virtuellen Photonen nur wenig zum Gesamtergebnis bei. Das liegt daran, dass die elektrische Wechselwirkung vergleichsweise schwach ist – je mehr Photonen ausgesandt und eingefangen werden, desto unwahrscheinlicher ist der jeweilige Prozess. Bei der starken Wechselwirkung ist das anders – die ist so stark, dass man nicht unbedingt annehmen kann, dass Prozesse mit 110 Gluonen unwahrscheinlicher sind als solche mit einem. Ich erwähne das hier nur, weil es wieder einmal zeigt, dass die Vorstellung mit den virtuellen Teilchen nicht unproblematisch ist.
Eine andere Darstellung der Masse
Insgesamt beschreiben wir unser Teilchen auf dem Weg von A nach B aber mit einer Formel, in der die (renormierte, also letztlich die experimentell gemessene) Masse drin steckt. Hätte es eine andere Masse, dann hätte es natürlich auch eine andere kinetische Energie; hätte es gar keine Masse, dann würde es sich mit Lichtgeschwindigkeit bewegen, jedenfalls, nachdem man über alle Möglichkeiten für den Weg von A nach B summiert hat. Die Masse bestimmt also, wie sich ein Teilchen von A nach B bewegt, und für jedes Wegstückchen, bei dem sich unser Teilchen auf einem geraden Weg mit konstanter Geschwindigkeit bewegt hat, konnten wir einfach diese Formel verwenden, um den Beitrag zur Gesamt-Wahrscheinlichkeit zu bestimmen.
Es ist also zunächst ziemlich überraschend, dass man den Weg eines Teilchens der Masse m von A nach B auch anders beschreiben kann. Man kommt nämlich genau zur selben Formel, wenn man annimmt, dass das Teilchen in Wahrheit gar keine Masse hat, aber dafür statt des einfachen Wegs auch Wege mit einem oder zwei oder beliebig vielen “Knicks” annimmt, wobei man an jedem Knick (sozusagen ein “Masseknoten”) einen Faktor m² einfügt. Dieses Bild, das ich schon mehrfach beim Thema “Higgs-Teilchen” verwendet habe, soll das illustrieren (im Bild steht an den Knoten nur ein m):
Mathematisch kann man wie folgt argumentieren: Für ein Teilchen mit Impuls k ist die entscheidende Formel (der Propagator) 1/(k²-m²), wobei m die Ruhemasse ist. Man kann dann schreiben:
Aus dem Propagator für ein Teilchen mit Masse wird also einer für eins ohne Masse mit unterschiedlich vielen Vertices dazwischen, von denen jeder einen Faktor m^2 bekommt.
Dabei habe ich von der Formel für die Reihenentwicklung Gebrauch gemacht und denke nicht mal ansatzweise darüber nach, wann die Reihe konvergiert, das können andere tun…
Falls sich jemand wieder über die Impulserhaltung an den Knicks Sorgen macht – das Problem haben wir im dritten Teil ja schon diskutiert.
Zunächst mal ist das nur ein komischer mathematischer Trick, der aber zeigt, dass wir uns unserer Vorstellung, was eine Masse ist, nicht all zu sicher sein sollten. (Achtung: Hier bitte nicht über die Wirkung der Masse im Schwerefeld nachdenken, denn unser Parameter m hier ist die Ruhemasse. Über die damit verbundene Begriffsverwirrung habe ich schon vor langer Zeit mal gebloggt.)
Aber mit mathematischen Tricks in der Physik ist das immer so eine Sache – auch die Formulierung mit dem Prinzip der kleinsten Wirkung (erinnert ihr euch noch an Teil 1 der Serie?) galt zunächst als mathematischer Trick ohne physikalische Bedeutung – und dann kam das Pfadintegral. Ein anderes Beispiel (über das ich endlich mal bloggen sollte) ist das Vektorpotential in der Elektrodynamik – ursprünglich ein mathematischer Trick, um Magnetfelder leichter beschreiben zu können, nahm es plötzlich im so genannten Aharonov-Bohm-Effekt ein Eigenleben an und ist auch heute aus der Quantentheorie nicht wegzudenken – die fundamentalen Gleichungen für Photonen enthalten das Vektorpotential (oder genauer, das Viererpotential) und nicht die “abgeleiteten” Größen Magnetfeld und elektrisches Feld, die wir aus der klassischen Physik kennen.
Es wäre also gar nicht verwunderlich, wen das mit dieser Um-Definition der Masse genauso wäre.
Das Higgs-Feld
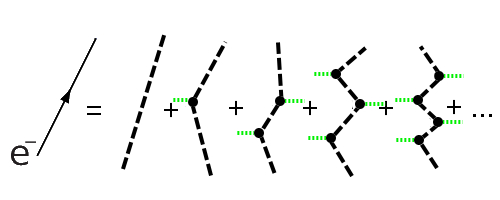
Und so ist es auch. Wir können das Bild mit den vielen “Masseknoten” oben auch anders interpretieren. Stellen wir uns vor, es gäbe ein geheimnisvolles, unsichtbares und unmerkbares Feld, das den ganzen Raum ausfüllt. (Klingt jetzt etwas esoterisch, oder?) Und unser masseloses Elektron kann auf seinem Weg von A nach B mit diesem geheimnisvollen Feld wechselwirken. Dann müssen wir auch dafür alle Möglichkeiten anschauen – solche, bei denen das Elektron gar nicht mit dem Feld wechselwirkt, oder einmal, oder zweimal usw. So würde das Ganze aussehen:
Solange dieses Feld also anders nicht wahrnehmbar ist, können wir ein masseloses Teilchen, das mit diesem Feld wechselwirkt, nicht von einem Teilchen mit Masse unterscheiden, das kein geheimnisvolles Feld um sich herum hat.
Als man in den Sechziger Jahren merkte, dass man die Theorie der schwachen Wechselwirkung nur dann vernünftig formulieren kann, wenn man annimmt, dass Teilchen wie Elektronen masselos sind, hat man genau diese Idee verwendet: Vielleicht gibt es ja so ein geheimnisvolles Feld, das den eigentlich masselosen Teilchen ihre Masse verleiht. Dieses Feld ist genau das berühmte Higgsfeld. Weil es überall ist und überall einen konstanten Wert hat, kann man es nicht messen. Man kann aber Störungen im Feld erzeugen (“Eine Erschütterung des Higgs-Feldes ich spüre”), die sich dann als Higgs-Teilchen bemerkbar machen. (Über Higgs-Teilchen habe ich schon ziemlich oft geschrieben, eine Übersicht findet ihr hier, oder ihr tippt einfach “Higgs” oben in die Suchbox ein.)
Im letzten Teil hatten wir ja die Masse renormiert, um die Beiträge von all den Prozessen loszuwerden, die wir eh nicht beobachten können. In Wahrheit (laut Standardmodell mit Higgs-Mechanismus) war es also gar nicht die Masse, die wir renormiert haben, sondern die Wechselwirkung mit dem Higgs-Teilchen. Da sich beide für uns gleich äußern, ändert das aber nichts,außer eben konzeptionell. (Ich kann mich nicht erinnern, das hier jemals in einem QFT-Buch gelesen zu haben – steht das irgendwo?)
Weitere Theorien
So, nun ist es aber wirklich genug. Jedenfalls für den Moment. Eigentlich müssten wir nälich auch noch gucken, was eigentlich auf der Quantenebene so alles mit dem Raum pasiert, durch den unser Teilchen von A nach B fliegt. Auch die Raumzeit ist ja – laut Allgemeiner RT – kein starres Gebilde, und wenn man Quanteneffekte berücksichtigt, dann müsste sie eigentlich ein unglaublich komplizierter Überlagerungs-Wirrwarr von allen möglichen Krümmungszuständen der Raumzeit sein. Bisher ist es aber nicht gelungen, eine solche Theorie aufzustellen, weil Theorien der Quantengravitation nicht renormierbar sind. (Anhänger der Stringtheorie weisen zwar gern darauf hin, dass die String-Theorie die Gravitation vorhersagt, aber das ist eine etwas gewagte behauptung: Die String-Theorie sagt ein masseloses Teilchen mir Spin 2 vorher. Quantisiert man die ART, dann sieht man, dass es auch dort ein masseloses Spin-2-Teilchen geben muss. Das grundlegende Problem, wie man die unendlichen Überlagerungen aller denkbaren Raumzeitstrukturen überlagert, wird von der Stringtheorie nicht mal adressiert – die Strings bewegen sich in der Theorie immer brav in einer unquantisierten Raumzeit. (Ich gebe zu, dass mein Wissenstand hier ein bisschen veraltet ist. Falls sich da in den letzten Jahren was getan hat, schreibt gern einen Kommentar.))
Leider habe ich auch keine Theorie der Quantengravitation. Deshalb ist die Serie hier zu Ende – jedenfalls fast. Denn einen Teil gibt es noch, in dem ich mir ein paar algemeinere Gedanken über die vielen unterschiedlichen Phänomene und Modelle, mit denen wir es hier zu tun hatten, machen möchte.
Warnung: Beim suchen nach Bildern bin ich auf eine Seite namens quantumfieldtheory.org gestoßen (ich setze extra keinen Link). Trotz des Namens, der klingt, als wäre das hier quasi die Haus-Seite aller QFTler, handelt es sich um eine dubiose Seite mit einer physikalischen Außenseitermeinung. Lesen auf eigene Gefahr…


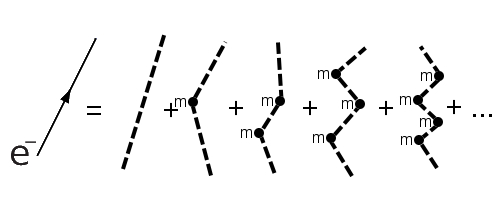







Kommentare (75)