Es ist also zunächst ziemlich überraschend, dass man den Weg eines Teilchens der Masse m von A nach B auch anders beschreiben kann. Man kommt nämlich genau zur selben Formel, wenn man annimmt, dass das Teilchen in Wahrheit gar keine Masse hat, aber dafür statt des einfachen Wegs auch Wege mit einem oder zwei oder beliebig vielen “Knicks” annimmt, wobei man an jedem Knick (sozusagen ein “Masseknoten”) einen Faktor m² einfügt. Dieses Bild, das ich schon mehrfach beim Thema “Higgs-Teilchen” verwendet habe, soll das illustrieren (im Bild steht an den Knoten nur ein m):
Mathematisch kann man wie folgt argumentieren: Für ein Teilchen mit Impuls k ist die entscheidende Formel (der Propagator) 1/(k²-m²), wobei m die Ruhemasse ist. Man kann dann schreiben:
Aus dem Propagator für ein Teilchen mit Masse wird also einer für eins ohne Masse mit unterschiedlich vielen Vertices dazwischen, von denen jeder einen Faktor m^2 bekommt.
Dabei habe ich von der Formel für die Reihenentwicklung 
Falls sich jemand wieder über die Impulserhaltung an den Knicks Sorgen macht – das Problem haben wir im dritten Teil ja schon diskutiert.
Zunächst mal ist das nur ein komischer mathematischer Trick, der aber zeigt, dass wir uns unserer Vorstellung, was eine Masse ist, nicht all zu sicher sein sollten. (Achtung: Hier bitte nicht über die Wirkung der Masse im Schwerefeld nachdenken, denn unser Parameter m hier ist die Ruhemasse. Über die damit verbundene Begriffsverwirrung habe ich schon vor langer Zeit mal gebloggt.)
Aber mit mathematischen Tricks in der Physik ist das immer so eine Sache – auch die Formulierung mit dem Prinzip der kleinsten Wirkung (erinnert ihr euch noch an Teil 1 der Serie?) galt zunächst als mathematischer Trick ohne physikalische Bedeutung – und dann kam das Pfadintegral. Ein anderes Beispiel (über das ich endlich mal bloggen sollte) ist das Vektorpotential in der Elektrodynamik – ursprünglich ein mathematischer Trick, um Magnetfelder leichter beschreiben zu können, nahm es plötzlich im so genannten Aharonov-Bohm-Effekt ein Eigenleben an und ist auch heute aus der Quantentheorie nicht wegzudenken – die fundamentalen Gleichungen für Photonen enthalten das Vektorpotential (oder genauer, das Viererpotential) und nicht die “abgeleiteten” Größen Magnetfeld und elektrisches Feld, die wir aus der klassischen Physik kennen.
Es wäre also gar nicht verwunderlich, wen das mit dieser Um-Definition der Masse genauso wäre.
Das Higgs-Feld
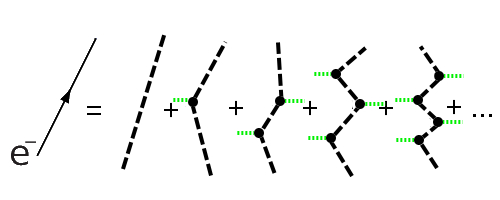
Und so ist es auch. Wir können das Bild mit den vielen “Masseknoten” oben auch anders interpretieren. Stellen wir uns vor, es gäbe ein geheimnisvolles, unsichtbares und unmerkbares Feld, das den ganzen Raum ausfüllt. (Klingt jetzt etwas esoterisch, oder?) Und unser masseloses Elektron kann auf seinem Weg von A nach B mit diesem geheimnisvollen Feld wechselwirken. Dann müssen wir auch dafür alle Möglichkeiten anschauen – solche, bei denen das Elektron gar nicht mit dem Feld wechselwirkt, oder einmal, oder zweimal usw. So würde das Ganze aussehen:
Solange dieses Feld also anders nicht wahrnehmbar ist, können wir ein masseloses Teilchen, das mit diesem Feld wechselwirkt, nicht von einem Teilchen mit Masse unterscheiden, das kein geheimnisvolles Feld um sich herum hat.
Als man in den Sechziger Jahren merkte, dass man die Theorie der schwachen Wechselwirkung nur dann vernünftig formulieren kann, wenn man annimmt, dass Teilchen wie Elektronen masselos sind, hat man genau diese Idee verwendet: Vielleicht gibt es ja so ein geheimnisvolles Feld, das den eigentlich masselosen Teilchen ihre Masse verleiht. Dieses Feld ist genau das berühmte Higgsfeld. Weil es überall ist und überall einen konstanten Wert hat, kann man es nicht messen. Man kann aber Störungen im Feld erzeugen (“Eine Erschütterung des Higgs-Feldes ich spüre”), die sich dann als Higgs-Teilchen bemerkbar machen. (Über Higgs-Teilchen habe ich schon ziemlich oft geschrieben, eine Übersicht findet ihr hier, oder ihr tippt einfach “Higgs” oben in die Suchbox ein.)
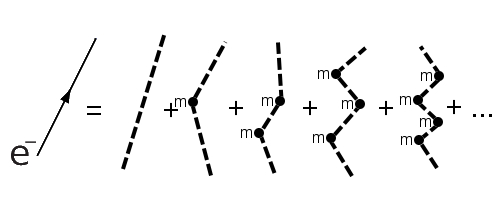
Kommentare (75)