Fazit: Anders als bei einer em-Welle kann ein einsames Punktteilchen von einer Gravitationswelle nichts bemerken, weil es die ganze Zeit im freien Fall ist.
Um die Wirkung einer Gravitationswelle zu verstehen, muss man also mehrere Teilchen betrachten und sehen, was diese Teilchen tun.
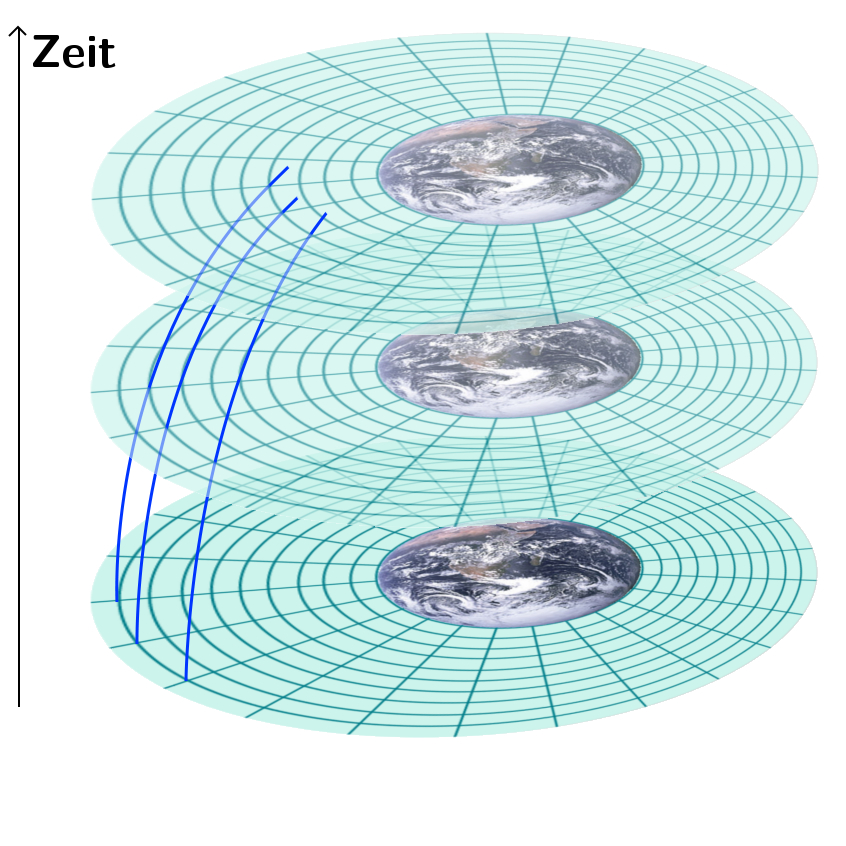
Betrachten wir erst mal drei Teilchen in der Nähe der Erde (die nachfolgenden Bilder stammen aus der Raumzeit-Krümmungs-Serie). Wir lassen sie in gleicher Entfernung nebeneinander starten und gucken, was passiert (hier ist in Richtung nach oben die zeit aufgetragen, die Erde habe ich dafür auf zwei Dimensionen plattgebügelt):
Wie ihr seht, laufen die Teilchen aufeinander zu – sie fallen alle in Richtung Erdmittelpunkt, ihr Abstand wird also kleiner. Die Linien starten senkrecht (am Anfang sind die Teilchen in Ruhe) und kippen dann immer weiter nach rechts ab, weil die Teilchen beim Fallen immer schneller werden.
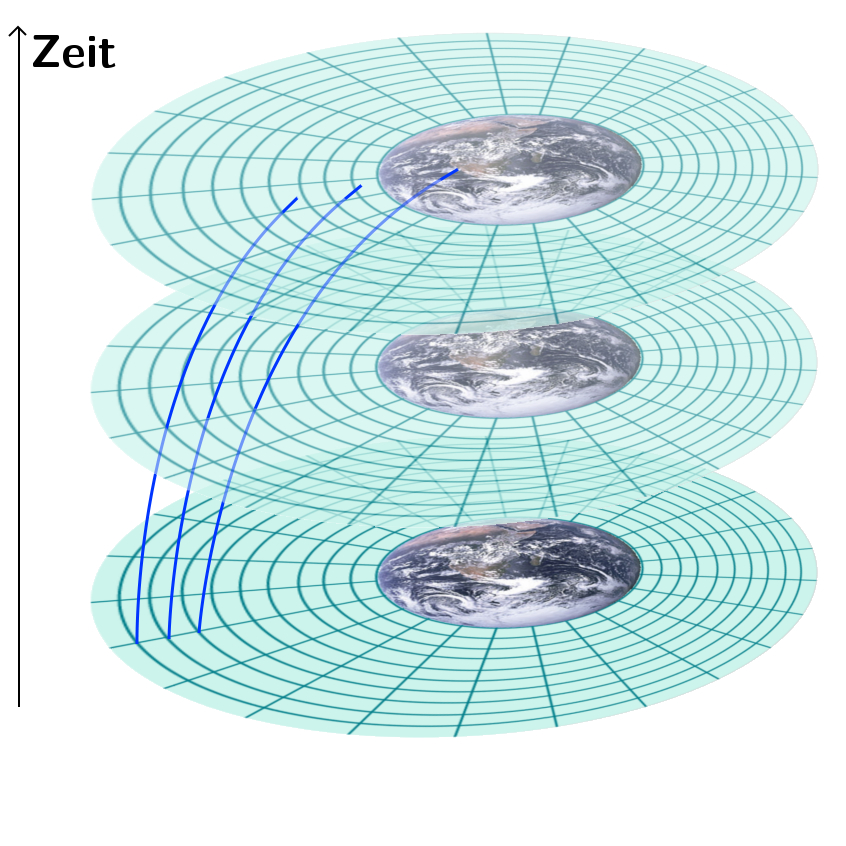
Lassen wir die drei Teilchen als nächstes in unterschiedlichem Abstand starten:
Das Teilchen, das dichter an der Erde dran ist, wird stärker angezogen (in der Sprache der Schwerefelder) und wird deswegen stärker beschleunigt. Die Teilchen entfernen sich also voneinander.
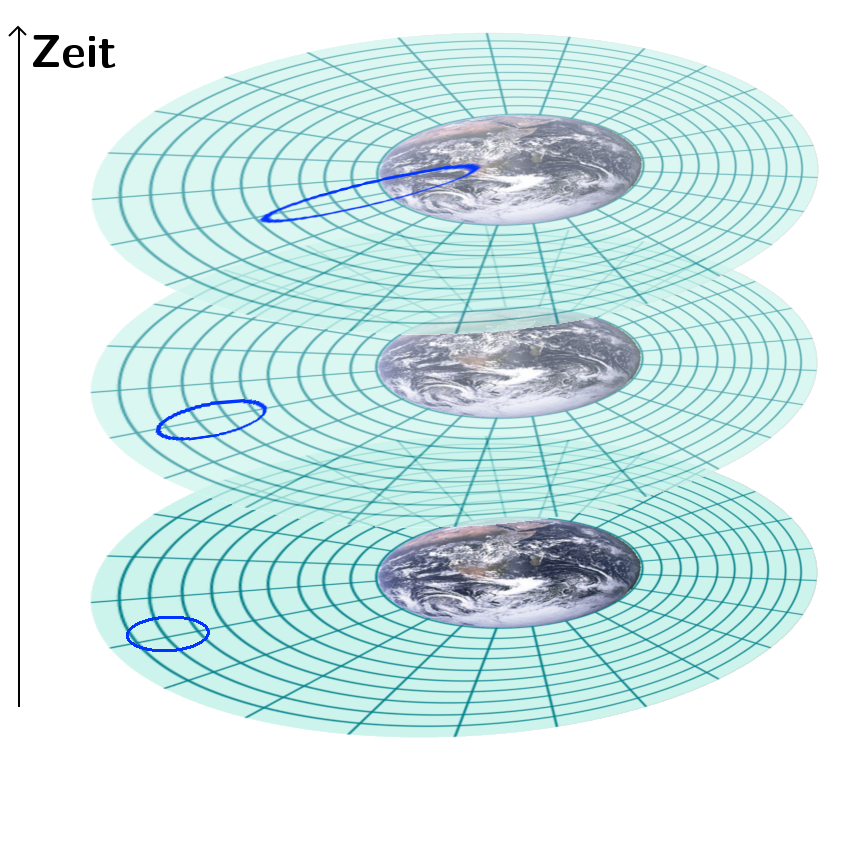
Wir können beide Bilder zusammenfassen, wenn wir zeichnen, was mit einem Ring aus Teilchen passiert:
Ein solcher Ring wird also verzerrt. Wenn man alles ganz sauber ausrechnet und aufzeichnet, dann sieht man, dass aus dem Ring eine Ellipse wird, wobei sich aber die Fläche nicht ändert.
Anders sähe die Sache aus, wenn wir den Teilchenring im Inneren der Erde loslassen würden (wir stellen uns vor, dass die Materie der Erde die Teilchen nicht weiter stört). Je dichter wir am Erdmittelpunkt sind, desto schwächer ist die Schwerkraft, also fallen weiter außen liegende Teilchen schneller. Nach wie vor fallen die Teilchen, die nebeneinander starten, aufeinander zu. Insgesamt wird dadurch der anfängliche Kreis kleiner, er wird also als ganzes gestaucht.
Das ist nicht nur hier so, sondern eine ganz allgemeine Regel für den Einfluss der Raumzeitkrümmung auf einen Teilchenring: Wird durch den Ring Materie eingeschlossen, dann wird er zusammengezogen und ändert seine Fläche – ein Ring im Vakuum kann durch die Raumzeitkrümmung (also durch Schwerefelder) zwar verzerrt werden, aber seine Fläche nicht ändern. Nachtrag: Nach längerem Überlegen bin ich (Dank an Niels et al.) zu dem Schluss gekommen, dass diese Aussage so nicht haltbar ist (siehe die Diskussion unten): Wenn ich es richtig sehe, gilt das Argument aber für eine Kugel aus Teilchen – eine Kugel aus Teilchen ändert – zumindest anfänglich – ihr Volumen nicht, wenn keine Materie eingeschlossen ist. (Wen sie sich dann erst mal verzerrt hat, dann kann sie auch ihr Volumen ändern.) Für einen Ring gilt das nur, wenn senkrecht zur Ebene des Rings nichts passiert wie bei einer Gravitationswelle, da hatte ich etwas zu schnell verallgemeinert. Siehe auch unten meinen Kommentar #17. (Mehr zum Überschussradius findet ihr im zweiten Teil der Serie – dort erkläre ich, warum der Sonnenradius “zu groß” ist.)
Zurück zu den Gravitationswellen. Um zu sehen, wie Gravitationswellen wirken, müssen wir uns also einen Ring aus Teilchen (oder eine andere Anordnung, aber ein Ring ist recht praktisch) im Vakuum angucken und Gravitationswellen draufschicken. (Die Frage, wo diese Wellen herkommen, klären wir später…) Hier ist unser Ring:
Wir stellen uns also einen Ring aus Teilchen vor, auf den eine Gravitationswelle trifft. (Man könnte auch eine Kugel nehmen, aber der Ring reicht, wie wir gleich sehen werden.) Die Welle trifft dabei senkrecht auf den Ring (stellt euch vor, eure Augen würden Gravitationswellen auf den Bildschirm strahlen), weil das am Einfachsten ist. Was kann so eine Welle mit dem Ring machen?
Dazu überlegen wir uns alle Möglichkeiten (ich hoffe, ich vergesse keine), wie sich so ein Ring verformen kann.







Kommentare (50)