Zunächst mal könnte er als ganzes größer oder kleiner werden, so dass der Durchmesser des Kreises oszilliert, er aber seine Form nicht ändert, etwa so (nach rechts ist hier die Zeit aufgetragen, wir gucken von Vorn auf den Ring, genau in der Richtung, in der auch die Welle auf den Ring trifft):
Das geht aber – wie eben schon erwähnt – im Vakuum nicht. Die einzige Möglichkeit, wie man es erreichen könnte, wäre, wenn man eine Masse “aus dem Nichts” entstehen lässt, dann würde sich eine Stoßwelle durch die Raumzeit ausbreiten, die unseren Ring als Ganzes stauchen oder (wenn die Masse verschwindet) dehnen könnte. Da nach Einstein aber E=mc² ist und da die Energie erhalten ist, geht das so nicht: Um Energie irgendwohin zu bekommen, muss man sie dorthin transportieren, man kann sie nicht einfach entstehen lassen. (Etwas Ähnliches gilt übrigens – wegen der Erhaltung der elektrischen Ladung – auch für elektrische Felder. Eine plötzlich entstehende elektrische Ladung würde eine elektrische Longitudinalwelle als Stoßwelle erzeugen, also eine, bei der das elektrische Feld in Ausbreitungsrichtung zeigt. Solche Wellen gibt es aber nicht.)
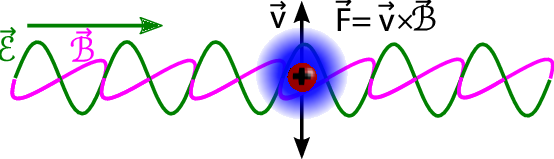
Die nächste Möglichkeit – und eine, die erst mal ganz plausibel aussieht – wäre die, dass wir unseren Ring zum Auf- und Abschwingen bringen. So wäre es ja mit einer elektromagnetischen Welle wie in diesem Bild hier (geklaut aus meinem demnächst erscheinenden Buch…):
Von links kommt eine em-Welle (elektrische Felder sind grün, Magnetfelder magenta) und bringt die elektrische Ladung in der Mitte zum Auf- und Abschwingen. Zusätzlich entsteht noch eine Kraft nach rechts, weil die bewegte Ladung eine Geschwindigkeit hat und das Magnetfeld darauf eine Kraft ausübt (das ist auch die Formel im Bild) – aber dieser Effekt ist klein und für uns nicht relevant (es ist der berühmte Lichtdruck).
Ein Ring aus elektrischen Ladungen würde also ebenfalls auf- und ab-schwingen. Kann ein Ring aus Massen in einer Gravitationswelle auch in dieser Weise auf- und abschwingen?
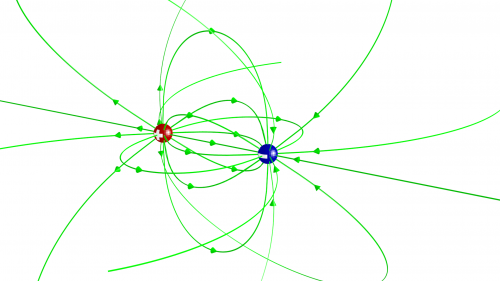
Dazu müssen wir uns fragen, wieso denn eigentlich das elektrische Feld in der em-Welle auf- und abschwingt. Eine em-Welle könnt ihr ja mit einer Antenne erzeugen, in der Elektronen mit ihrer elektrischen Ladung auf und ab beschleunigt werden und oszillieren. Weil so eine Antenne etwas unübersichtlich ist (es gibt viele Elektronen drin und positive Atomkerne, die die Gesamtladung ausgleichen), nehmen wir stattdessen den einfachsten Fall: Wir denken uns eine positive und eine negative Ladung gleicher Stärke, einen sogenannten Dipol. Die haben ein elektrisches Feld, das etwa so aussieht:
Die Feldlinien zeigen dabei von der positiven zur negativen Ladung. Um mit einem solchen Dipol eine em-Welle zu erzeugen, können wir die beiden Ladungen zum Beispiel mit einer (ungeladenen) Feder verbinden und dann schwingen lassen. Weil die beiden Ladungen entlang einer Achse schwingen, entsteht ein passend dazu gerichtetes elektrisches Feld (jedenfalls, wenn man senkrecht zur Verbindungslinie nach außen guckt), das ebenfalls schwingt, also unsere em-Welle. Deswegen heißt eine solche Welle auch Dipol-Welle. (Mathematisch ist unser Dipol-Moment der Abstand zwischen den Ladungen multipliziert mit der Ladungsstärke. Die Stärke der entstehenden Welle ist dann proportional zur Ladungsstärke mal der Beschleunigung, also der zweiten Ableitung des Abstands nach der Zeit.)
Versuchen wir dasselbe mit Massen. Wir verbinden also zwei Massen mit einer Feder und lassen sie schwingen. Bekommen wir eine Gravitationswelle?
Leider nein. Beim elektrischen Dipol hatten die beiden Ladungen ja entgegengesetztes Vorzeichen – eine war positiv und eine negativ. Beim Massen-Dipol ist das anders: Massen gibt es nur mit einem Vorzeichen (es gibt keine “Anti-Masse”). Betrachtet man jetzt den Effekt der Schwingung, dann hebt die Bewegung der einen Masse genau die der anderen Masse auf. (Der Grund dafür ist das 3. Newtonsche Axiom: Auch beim Massendipol ist die Stärke gleich der zweiten Ableitung nach der Zeit, aber die Summe über alle Beschleunigungen im System ist wegen F=ma und “actio=reactio” immer gleich Null.) Nachtrag: Dieser Absatz ist nicht ganz richtig. Wir bekommen tatsächlich keine Gravitationswelle durch ein Dipolmoment – das verschwindet, insofern ist die Erklärung richtig. Aber die schwingenden Massen haben ein “Quadrupolmoment” (klingt komisch, weil es ja zwei sind, nicht vier, ist aber so) und senden deshalb trotzdem Gravitationswellen aus. Das, worum es mir ging (Gravitationswellen haben keinen Dipol-Charakter) ist also richtig, aber dass die schwingenden massen gar keine Wellen aussenden, ist falsch. Dank an Markus Pössel, der es mir geduldig erklärt hat.








Kommentare (50)