Eine Gravitationswelle kommt also nicht durch einen Massendipol zu Stande. Entsprechend können wir unseren Ring nicht als ganzes nach oben oder unten verschieben.
Das nächst-kompliziertere Verformungsmuster für unseren Ring ist, ihn in eine Ellipse mit gleicher Fläche zu verzerren. (Die Fläche darf sich ja nicht ändern, wie wir oben gesehen haben – ich gebe aber zu, dass ich beim Zeichnen nicht ganz exakt war…).
Der Ring oszilliert also jeweils zwischen zwei Ellipsenformen, zwischendurch ist er aber immer auch mal unverformt. Auf der schönen Seite Einstein online (generell eine gute Adresse, wenn es um die Relativitätstheorie geht) gibt es dazu auch eine schicke Animation (Dank an Markus Pössel):
Breitet sich so eine Verzerrung aus, dann sieht das etwa so aus:
Natürlich kann die Ellipse auch gedreht sein, etwa so:
Die einzelnen Teilchen bewegen sich dabei nur wenig.
Diese beiden um 45° zueinander gedrehten Möglichkeiten reichen schon, um alle denkbaren Orientierungen der Ellipsen zu bekommen; wenn ihr einen anderen Winkel wollt, dann könnt ihr die beiden Ellipsen passend überlagern. (Das ist ganz analog zu einer em-Welle – auch dort gibt es zwei Möglichkeiten für das elektrische Feld: Es kann entweder senkrecht oder waagerecht schwingen, andere Orientierungen bekommt ihr ebenfalls durch Überlagerung.) Wellen dieser Art nennt man auch Quadrupol-Wellen.
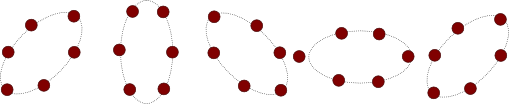
Man kann die beiden Ellipsen aber auch zeitversetzt überlagern, dann bekommt man so ein Muster:
Dieses Bild kann man leicht falsch verstehen: Die einzelnen Teilchen rotieren nicht mit dem Ring, sondern beschreiben nur kleine Kreisbahnen um ihre Position herum.
Auch hier gibt es wieder zwei Möglichkeiten – die Ellipse kann sich links- oder rechtsrum drehen. Wichtig ist dabei, dass die einzelnen Teilchen des Rings nicht um den ganzen Ring herumrotieren, sondern alle nur kleine Bewegungen um ihre Ruhelage machen. Auch die rotierende Ellipse ist wieder ganz analog zur em-Welle: Auch dort kann man durch zeitlich verschobene Überlagerung eine sogenannte zirkular polarisierte Welle bekommen, die sieht so aus:
Auch diese Welle kann sich entweder mit dem oder gegen den Uhrzeigersinn drehen.
Die Orientierung der Welle bezeichnet man generell als ihre Polarisation. Dass es letztlich nur zwei Möglichkeiten für diese Polarisation gibt, hängt damit zusammen, dass die Welle sich mit Lichtgeschwindigkeit ausbreitet und dass ihr sie deshalb nicht überholen könnt. Bei der Lichtwelle bekommt ihr übrigens in allen Fällen eine identisch aussehende Welle, wenn ihr das Bild um 360° dreht; bei der Gravitationswelle schon, wenn ihr es um 180° dreht. (Wenn ihr den Sprung zur Quantentheorie macht, ist das genau der Grund, warum Photonen einen Spin von 1 haben müssen und Gravitonen einen von 2. Mehr zum Thema Teilchenspin findet ihr hier und hier. Und da man auch Gravitonen nicht überholen kann, haben die auch nur zwei mögliche Zustände des Spins; Spin-2-Teilchen mit Masse hätten 5 Möglichkeiten. Hmmm, über Gravitonen habe ich noch nie geschrieben, aber das werde ich hoffentlich bald mal nachholen, dann verstehe ich die Dinger vielleicht mal….)
Dass ich so detailliert auf dieses Verformungsmuster unseres Rings eingehe, lässt schon ahnen, dass das jetzt tatsächlich mal eine Verformung ist, die mit Gravitationswellen auch möglich ist – und so ist es auch. Dazu dürfen die Massen nicht bloß gegeneinander schwingen, sondern müssen umeinander herum rotieren, etwa so:

By User:Zhatt – Own work, Public Domain, Link
Dabei entstehen dann Gravitationswellen; das veranschaulicht diese Animation der NASA (zwei oszillierende Neutronensterne sitzen in der Mitte und strahlen die Wellen nach Außen ab):

By NASA/JPL – https://lisa.jpl.nasa.gov/popups/ripples.html
https://lisa.jpl.nasa.gov/IMAGES/wavy.gif, Public Domain, Link
Eine sehr schöne Animation (auf allerdings augenentzündungenverursachendem (ein Wort von geradezu Homerscher Länge…) Hintergrund) findet ihr auch auf dieser Seite.
Auch in unserem Sonnensystem entstehen solche Wellen, weil die Planeten um die Sonne kreisen. Allerdings sind sie unglaublich schwach – Das System Sonne-Jupiter beispielsweise strahlt etwa 40Watt an Gravitations-Energie nach außen ab (die Strahlungsleistung der Sonne beträgt etwa 4E26Watt, also 100 Billionen Billionen Mal so viel – kein Wunder, dass wir Sterne leicht sehen können, aber nicht so viel von ihren Gravitationswellen bemerken…).









Kommentare (50)