Als Kind und Jugendlicher hatte ich eine Schwäche für Monsterfilme – Ungeheuer wie King Kong, Gamera, den Rhedosaurus (“the beast from 20000 fathoms”) fand ich faszinierend (für jemanden, der Dinos mag, wohl nicht sehr ungewöhnlich). Eins der bekanntesten dieser Filmmonester ist sicherlich Godzilla – der vor ziemlich genau 60 Jahren zum ersten Mal auf der Leinwand zu sehen war. Da das hier ja kein Film-Kritik-Blog ist, nutze ich dieses Jubiläum (und den gerade anlaufenden Kinofilm), um ein wenig über die wissenschaftliche Seite von Godzilla nachzudenken.
Zum Glück ist dieses Thema in der wissenschaftlichen Literatur bereits intensiv untersucht worden, und zwar anlässlich des Godzilla-Fils von 1998 (in dem Godzilla allerdings eher ein riesiger Theorpode war als das behäbige Monster aus den 50ern, was vermutlich zum einen am Einfluss von Jurassic Park lag und zum anderen daran, dass man keine Sumo-Ringer in Gummi-Kostüme stecken musste, so dass man bei den Proportionen des Körpers und seinen Bewegungen etwas freier war… – die früheren amerikanischen Monsterfilme bedienten sich ja stattdessen der Stop-Motion-Technik von Willis O’Brien und seinem Schüler Ray Harryhausen). In dieser Arbeit untersuchte Per Christiansen das Filmmonster, indem er die Eigenschaften von Raubsauriern hochrechnete. Dazu verwendete er ein Modell des Monsters, so dass er genaue Messungen der Proportionen und des Volumens machen konnte. Dabei stellt sich – wenig überraschend – heraus, dass der amerikanische Godzilla biomechanisch nicht besonders plausibel ist.
Der Godzilla von 1998 ist aber mit 60-90 Metern Höhe, wenn er sich aufrichtet, geradezu ein Zwerg gegenüber dem aktuellen Godzilla, der eine Höhe von etwa 120-150 Metern hat, wie ich dieser Internetseite entnehme. (Ich zeige hier lieber keine Godzilla-Bilder – Filmfirmen verstehen ja bei Copyright-Verletzungen eher wenig Spaß und frei verfügbare Bilder habe ich keine gefunden.) Leider habe ich kein Modell des Monsters zur Hand – aber da es hier eh nur um Abschätzungen geht (endlich mal wieder ein Fermi-Problem), macht das nicht viel.
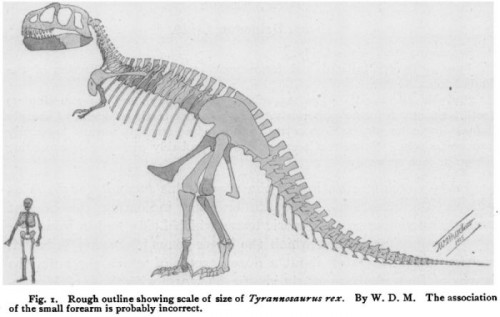
Fangen wir mit der Körpermasse an. Mit einer Höhe von etwa 120 Metern ist Godzilla etwa 20 Mal so hoch wie ein Tyrannosaurus rex, wenn der sich aufrichtet, so wie man ihn früher gern dargestellt hat (als er noch deutlich Godzilla-artiger aussah):
(Bild von Scientific American.)
Die genaue Masse eines T. rex ist natürlich nicht bekannt, aber die besten Schätzungen liegen bei etwa 6-9 Tonnen (sehr genaue Untersuchungen dazu gibt es von John Hutchinson). Nehmen wir einen Wert im etwas höheren Bereich, weil Godzilla ja recht massig gebaut ist, von 8 Tonnen.
Mit 120 Metern Höhe ist Godzilla etwa 20 Mal so hoch wie ein T. rex, also ist er 8000 mal schwerer (denn das Volumen ist proportional zur Länge hoch drei). Das macht dann satte 64000Tonnen. Bei 150 Metern Höhe landen wir bei etwa dem Doppelten, nämlich 125000 Tonnen. Das ist – wenn ich mich nicht total vertue – etwa die Masse eines Flugzeugträgers. Ein ziemlicher Brocken also. (Christiansen kommt für den 1998er Godzilla mit 91 Metern Körperhöhe auf eine Masse von etwa 23000 Tonnen – im paper steht 23821.9; BiologInnen haben das mit dem Sinn von signifikanten Stellen manchmal nicht so im Griff – wenn ich die Höhe nur auf drei Stellen genau kenne, kann ich die Masse kaum auf 6 Stellen genau berechnen..)
Diese Masse muss der gute (oder böse?) Godzilla natürlich auch mit sich herumschleppen, und zwar auf seinen Beinen. Wenn ich mir die Godzilla-Bilder so ansehe, dann hat Godzilla Beine, die einen Durchmesser von so etwa 15 Metern haben. Muskeln braucht er auch noch, also nehmen wir mal an, dass vielleicht die Hälfte der Bein-Fläche auf Knochen entfällt (das ist allerdings ziemlich viel…). Das macht dann einen Knochen-Querschnitt von 88m².
Wenn Godzilla einen Schritt macht, dann lastet das ganze Gewicht auf einem Bein – gut, beim aktuellen Godzilla wird ein Teil von Schwanz getragen, der ja anscheinend auf dem Boden schleift. Nehmen wir mal an, dass 100000 Tonnen übrig bleiben, die das Bein zu tragen hat, das wäre dann eine Gewichtskraft von (ich nehme jetzt die vereinfachte Exponentialschreibweise) 10m/s² (für die Erdbeschleunigung) mal 1E5 Tonnen oder 1E8 Kilogramm also 1E9 Newton. Die müssen wir auf die knapp 100m² Fläche verteilen, was eine Druckspannung von 10Megapascal ergibt. Das scheint zunächst ganz in Ordnung – Knochen können Drucklasten von bis zu 250MPa ertragen. Allerdings sind die Lasten beim Gehen tatsächlich deutlich größer – auch bei großen Tieren, die ihre Gliedmaßen sehr gerade halten wie Elefanten, werden die Knochen auf Biegung belastet, so dass typische Lasten deutlich größer sind. (Beim Menschen treten die größten Lasten bei Bewegungen wie dem Treppensteigen auf – da ist die Knochenlast etwa das 5-7-fache des Körpergewichts.) Das scheint tatsächlich immer noch machbar – allerdings muss man auch berücksichtigen, dass das Biegemoment, das auf den Knochen wirkt, diesen auch auf Zug belastet, und die Zugfestigkeit von Knochen ist mit etwa 150MPa deutlich kleiner.






Kommentare (29)