Christiansen kommt für den “amerikanischen” Godzilla von 1998 zu ähnlichen Ergebnissen – er verwendet eine Beziehung für die Biegefestigkeit des Knochens und zeigt, dass dieser Godzilla in einem Bereich liegt, wie man ihn für sehr behäbig bewegte Tiere erwarten würde. Trotzdem – tragen können die Knochen die Masse des Tieres, woran man nebenbei mal wieder sieht, dass Knochen ein ziemlich leistungsfähiges Material sind. Allerdings könnte das Problem deutlich schwerwiegender werden, wenn man sich die Füße und Zehen anguckt – je nachdem, ob Godzilla mit dem ganzen Fuß auftritt oder Zehengänger ist. Als Zehengänger dürfte er Probleme bekommen – die Zehen werden stark auf Biegung belastet und haben einen deutlich kleineren Querschnitt. (Falls ich den Film demnächst gucke – lohnt sich das? – sollte ich wohl mal drauf achten…)
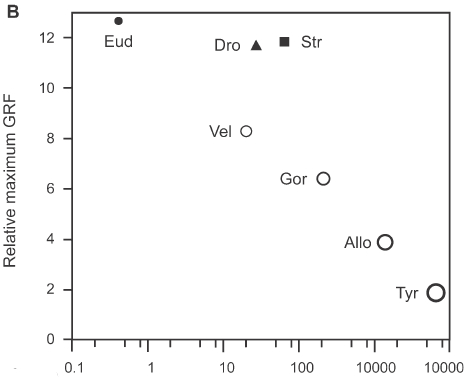
Deutlich problematischer wird die Sache allerdings, wenn wir uns die zum Bewegen erforderlichen Muskeln ansehen. Zu diesem Problem (für Dinosaurier, nicht für Film-Monster) habe ich ja sogar selbst mal geforscht. Damals haben wir untersucht, welche maximale Kraft ein zweibeiniger Dino beim Laufen ausüben kann – die sollte natürlich schon etwa so groß sein wie das Körpergewicht. Hier eine der Grafiken aus unserer Arbeit:
Zu sehen ist auf der vertikalen Achse die maximale kraft in Einheiten des Körpergewichts, auf der horizontalen Achse die Körpermasse in Kilogramm. Nach dieser Grafik dürfte bei etwa 100 Tonnen Körpermasse Schluss sein – danach ist das Tier nicht mehr in der Lage, sein Gewicht zu halten. Wir haben damals das Laufen untersucht, bei dem die Beine ja ein wenig eingeknickt sein müssen, während sie beim Gehen ja gestreckt sind. Außerdem sind beim Gehen ja häufig beide Beine auf dem Boden, so dass sich die Masse verteilt. Direkt übertragen kann man die Grafik für ein gehendes Tier also nicht (ich vermute mal, der neue Godzilla rennt nicht herum oder hüpft akrobatisch durch die Gegend wie der King Kong von Peter Jackson, der ja quasi schwerelos zu sein schien – mal ganz davon abgesehen, dass die Fenstersimse in New York anscheinend aus ultrahochverdichtetem Terkonitstahl sind, wenn sich da ein schwingender Gorilla langhangeln kann.). Trotzdem muss natürlich auch ein gehendes Tier seine Körpermasse mit Muskelhilfe tragen – spätestens dann, wenn der Schritt gemacht ist, bei dem man ja leicht nach vorn fällt, müssen auch die Muskeln ihren Beitrag leisten. Selbst wenn er dann nur 1% seiner Körpermasse mit den Muskeln tragen muss, wäre das schon zu viel. Mit normalen Muskeln dürfte Godzilla sich also nicht bewegen können – da er aber ja radioaktiv strahlt und eh nen Kernreaktor eingebaut hat (das hat er doch hoffentlich?), hat er ja vielleicht auch spezielle Muskeln, die extra-hohe Kräfte erzeugen können.
Ein anderes Problem der Körpermasse tritt auch beim Gehen auf – der Boden muss das Tier ja auch tragen können. Wenn wir mal annehmen, dass die Füße beim Gehen eine Bodenberührung haben, die etwa dem oben berechneten Durchmesser des Beins entspricht (das scheint zu den Bildern zu passen), dann wird beim Gehen auch der Boden punktuell mit Spannungen von etwa 10MPa belastet. Beton hat eine Druckfestigkeit von 20MPa oder mehr – aber trotzdem dürfte man erwarten, dass auch Straßen unter Godzillas Schritten rissig werden. Wie er aus dem Meer spazieren kann, wo der Boden ja vermutlich weicher Sand oder Schlick ist, weiß ich nicht – eigentlich müsste man ihn dort extrem tief einsinken sehen.
Wie viel Energie braucht eigentlich so ein Riesenmonster? Das hängt natürlich davon ab, was Godzilla für eine Stoffwechselrate hat. Ist er ein Warmblüter, dann ist sein Energieverbrauch höher als bei einem wechselwarmen Tier. Für den T. rex gibt es ja eine berühmte Abschätzung, nach der er als wechselwarmes Tier etwa 73 Rechtsanwälte pro Jahr fressen muss, als Warmblüter etwa 292. Um das hochzurechnen, muss man die entsprechende Beziehung für den Energieverbrauch als Funktion der Körpermasse verwenden. Diese Beziehung wurde natürlich an aktuell lebenden Tieren ermittelt, so dass insbesondere bei den wechselwarmen Tieren nur vergleichsweise niedrige Massenwerte zur Verfügung stehen, insofern sind diese Abschätzungen natürlich recht ungenau.






Kommentare (29)