Zunächst einmal gilt in der Quantenmechanik die (etwas seltsam anmutende) Regel, dass es einerseits Zustände mit genau definierter Energie gibt und andererseits solche, bei denen die Energie nicht “scharf” definiert ist. (Mehr über Zustände in der Quantenmechanik erfahrt ihr in dieser Serie.) Zustände, bei denen die Energie einen eindeutigen, genauen Wert hat, sind gleichzeitig auch stationär, sie hängen also nicht von der Zeit ab. (Für PedantInnen: Ja, bis auf einen Phasenfaktor…) Da wir uns hier für die Energien interessieren, betrachten wir nur Zustände, deren Energie eindeutig ist.
Dabei ist die Energie eines solchen Systems aus zwei Atomen nicht mehr beliebig, sondern quantisiert (deswegen heißt es ja auch Quantenmechanik) – sie kann also nur ganz bestimmte Werte annehmen. Ihr könnt also keine beliebigen Schwingungsenergien mehr bekommen (so wie in der klassischen Physik), sondern nur ganz bestimmte. Bezeichnet ihr die Schwingfrequenz mit dem Buchstaben ν (griechisch “nu”, nicht “vau”), dann gilt die Regel, dass ihr dem System Schwingungsenergie nur in Paketen der Größe hν (oder Vielfachen davon) zuführen könnt; h ist dabei das Plancksche Wirkungsquantum.
Wenn das System also ein bisschen schwingt, dann könnt ihr es – anders als in der klassischen Physik – nicht ein ganz winzig kleines bisschen mehr schwingen lassen, sondern eben nur die Energie um mindestens hν erhöhen. (Sehr ausführlich habe ich dieses System auch in meiner QFT-Serie besprochen.) Planck hat diese Idee der Quantisierung von Molekülschwingungen übrigens eingeführt, um damit das Lichtspektrum von erhitzten Körpern zu erklären. Für ihn war das allerdings nur ein reines ad-hoc-Modell (die Quantenmechanik gab es damals noch nicht, die fing erst mit dieser Idee an), denn zu dieser Zeit glaubte er eigentlich noch nicht, dass die Materie aus Atomen aufgebaut ist, sondern nahm an, sie sei kontinuierlich.
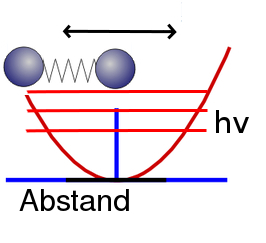
Zeichnet man ein paar der Energieniveaus in das Bild ein, dann sieht das etwa so aus (das hν kennzeichnet den Abstand zweier Niveaus):
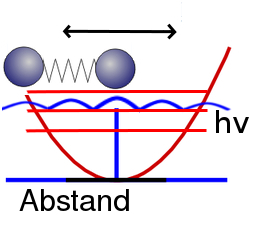
Hat unser schwingendes Molekül eine bestimmte Schwingungsenergie (wobei eben nicht jede beliebige Energie möglich ist, sondern nur ganz bestimmte Energien), dann gehört dazu eine Wahrscheinlichkeitsverteilung: Der Abstand zwischen den Molekülen ist nicht eindeutig definiert, stattdessen gibt es eine Wahrscheinlichkeit dafür, einen bestimmten Abstand zu messen. Weil zu großen Abständen der Moleküle große Energien gehören, ist die Wahrscheinlichkeit, einen großen Abstand zu messen, groß, wenn die Energie groß ist, und klein, wenn die Energie klein ist. Umgekehrt findet ihr bei kleiner Energie die beiden Moleküle eher etwa im Gleichgewichtsabstand. (Ich erkläre das hier nur sehr grob, Details könnt ihr auch in meiner Serie zur Schrödingergleichung (siehe die Artikelserien) nachlesen, allerdings nicht für ein schwingendes Molekül, die Logik ist aber immer dieselbe.) Hier habe ich das – ziemlich grob und schematisch – für eins der Energieniveaus in blau eingezeichnet:
(Dass die Wahrscheinlichkeit für die Abstände nicht einfach nach Außen hin abfällt, sondern dass es immer Maxima und Minima gibt, ist ganz normal und hat etwas mit dem Wellencharakter der Materie zu tun. Ihr braucht euch darüber hier aber keine Gedanken zu machen, denn für das Thema Nullpunktsenergie spielt das keine große Rolle.)
Je niedriger die Energie unseres schwingenden Moleküls ist, desto wahrscheinlicher ist es also, dass wir als Abstand der beiden Moleküle in etwa den Gleichgewichtsabstand finden.Wenn wir die Energie also immer weiter verkleinern, dann sollten wir die beiden Atome mit immer höherer Wahrscheinlichkeit im Gleichgewichtsabstand finden.
(Anmerkung für die ganz Genauen: Ich schreibe hier extra “in etwa”, weil bei ungeraden Quantenzahlen die Wahrscheinlichkeit des Gleichgewichtsabstandes verschwindet, die Wellenfunktion hat hier einen Knoten)
Und was ist, wenn wir die Energie so niedrig machen, wie es überhaupt nur geht? Wenn wir also dem schwingenden Molekül seine Schwingungsenergie vollkommen entziehen – soweit das eben möglich ist? Dann sollte es logischerweise Energie Null haben (wobei der Energienullpunkt durch das Minimum der Energiekurve oben definiert ist). Die beiden Atome wären dann genau im Gleichgewichtsabstand.






Kommentare (34)