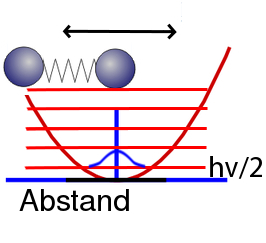
Das scheint ganz plausibel, ist aber falsch: Der Zustand mit der niedrigsten Energie hat eine höhere Energie als das Minimum unserer Kurve. Sie beträgt hν/2. Während ihr einem klassischen System alle Schwingungsenergie entziehen könnt, ist das bei einem quantenmechanischen Schwinger nicht möglich, da bleibt immer etwas Schwingungsenergie übrig. So etwa sehen die Energieniveaus aus:
In blau habe ich wieder die Wahrscheinlichkeit aufgetragen, allerdings nicht ganz maßstabsgetreu.
Man kann sich diese Wahrscheinlichkeitsverteilung auch über die berühmte Unschärfe-Relation erklären: Wenn die beiden Atome genau den Gleichgewichtsabstand haben, dann kennen wir ihren Ort perfekt genau (jedenfalls relativ zueinander) – ebenso aber ihre Geschwindigkeit, weil die beiden ja in Ruhe sind. Das ist aber nicht möglich.
Die Energie ist also in unserem quantenmechanischen Schwinger nie ganz so niedrig, wie sie es in der klassischen Physik sein könnte, sondern etwas größer. Das ist die berühmte Nullpunktsenergie, die Energie, die auch dann da ist, wenn wir unser System auf den absoluten Nullpunkt abkühlen, so dass es alle Energie abgegeben hat, die es abgeben kann.
Ist diese Nullpunktsenergie für irgendetwas relevant? Wenn ich sie dem System nicht entziehen kann, dann kann ich ja immer nur Änderungen relativ zur Nullpunktsenergie betrachten – ich kann dem System Energie (in Paketen der Größe hν) zuführen oder wieder entziehen, aber an der Nullpunktsenergie ändert sich nichts. Ich kann im Zweifel ja einfach meinen Energie-Nullpunkt ein bisschen nach oben verschieben, und dann ist wieder alles gut. Insofern sollte die Nullpunktsenergie eines Moleküls eigentlich ziemlich irrelevant sein – sie ist sicherlich interessant, aber eher was für Theorie-Fans, oder?
Wenn ihr das denkt, dann seid ihr vermutlich in guter Gesellschaft – die meisten Physikbücher, die ich kenne, erwecken zumindest den Eindruck, dass die Nullpunktsenergie in solchen schwingenden Systemen nicht besonders wichtig ist, und ich selbst habe das auch bis vor kurzem gedacht.
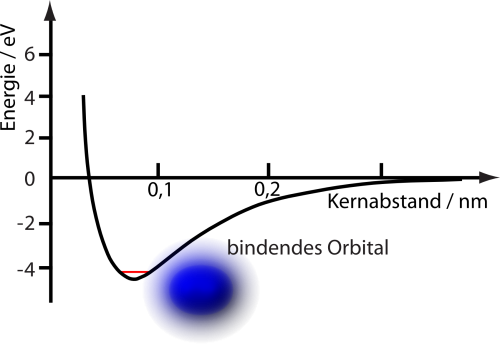
Um zu sehen, warum die Nullpunktsenergie doch wichtig sein kann, stellt euch vor, ihr wolltet die Eigenschaften unseres Moleküls berechnen, also insbesondere auch seine Bindungsenergie. Was man dazu tun kann, ist, das Verhalten der Elektronen des Moleküls für verschiedene feste Abstände der beiden Atomkerne zu analysieren und die zugehörige Energie zu berechnen, so wie in dem Bild ganz oben. Das ist eine sinnvolle Methode, weil die Atomkerne ja verglichen mit den Elektronen sehr schwer sind – die Dynamik der Elektronen ist für die chemische Bindung eben viel wichtiger als die der Kerne. Daran könnt ihr jetzt die Energie des Moleküls ablesen, es ist logischerweise die Energie im Minimum.
Oder auch nicht. Denn die beiden Atomkerne könnten ja auch gegeneinander schwingen – und damit gibt es eine Nullpunktsenergie. Der tatsächliche Zustand niedrigster Energie liegt also etwas höher als das Minimum, das ihr gerade berechnet habt. Und das muss man berücksichtigen, wenn man zum Beispiel die Struktur von Molekülen oder chemische Reaktionen anguckt. Für das Wasserstoffmolekül beträgt die Energieänderung durch die Nullpunktsenergie etwa 0,27 Elektronenvolt (wenn ich die Zahlen auf dieser Seite richtig verwendet habe; das Elektronenvolt ist einfach eine Energieeinheit, die in der Atomphysik praktisch ist, weil dann handliche Zahlenwerte herauskommen). Zeichnet man diese Energie in unser Bild von ganz oben ein, sieht das so aus (ehrlich gesagt, bin ich mir nicht 100% sicher, dass das Bild so stimmt – es mag sein, dass in der schwarzen Kurve die Nullpunktsenergie schon enthalten war; da ich momentan keinen Zugriff auf die Quelle habe, aus der die Kurve stammt, kann ich das nicht genau sagen):
Wenn ihr also zum Beispiel eine chemische Reaktion berechnet, bei der sich ein Wasserstoffmolekül bildet, dann dürft ihr eben nicht einfach die Energie im Minimum der Kurve verwenden, sondern müsst berücksichtigen, dass die tatsächliche Bindungsenergie etwas kleiner ist. (Das Energieniveau liegt etwas höher, die zugehörige Energie, die ich bekomme, wenn ich von einem Zustand mit Energie Null in dieses Niveau gehe, ist also kleiner.) Die Nullpunktsenergie hat also tatsächlich messbare Konsequenzen, wenn es sie nicht gäbe, würden sich die Bindungsenergien von Molekülen entsprechend ändern.






Kommentare (34)