Direkt nachmessen können wir die Nullpunktsenergie natürlich nicht (wir können dem Molekül nicht seine Schwingungsmöglichkeit wegnehmen, so dass es dann das echte Minimum der Kurve erreicht), aber ohne die Nullpunktsenergie gäbe es eine Diskrepanz zwischen der berechneten und der tatsächlichen Bindungsenergie von Molekülen.
Wichtig wird das zum Beispiel in der Halbleiterphysik: Zinkoxid ist ein Halbleiter, der sich dadurch auszeichnet, dass er eine sehr große Energielücke zwischen den besetzten und den unbesetzten Zuständen der Elektronen hat. Er ist deshalb für sichtbares Licht durchsichtig und kann darum zum Beispiel verwendet werden, um Kontakte für Leuchtdioden oder Solarzellen herzustellen. Reines Zinkoxid ist ein sogenannter n-Halbleiter, also einer, bei denen Elektronen den Strom tragen (Bei p-Halbleitern sind es Fehlstellen, so genannte Löcher, die für die Leitung verantwortlich sind.) Warum Zinkoxid ein n-Halbleiter ist, ist allerdings nicht ganz klar. Eine Möglichkeit besteht darin, dass das Material bei der Herstellung Wasserstoff einlagert, der dann Elektronen abgeben kann. Um die Energien für die Einlagerung von Wasserstoff zu berechnen, muss man die Energie des Wasserstoffs im Material mit der von molekularem Wasserstoff vergleichen – und genau dabei kommt die Nullpunktsenergie ins Spiel. Nur wenn man die berücksichtigt, ergeben sich korrekte Werte für die Energien. Die Berechnungen zeigen, dass es tatsächlich plausibel ist, dass Wasserstoff für die Eigenschaften von Zinkoxid verantwortlich ist – allerdings ist das nicht eindeutig geklärt.
Die Nullpunktsenergie ist vor allem dann wichtig, wenn ihr zwei Zustände vergleicht, die sich in ihren Schwingungsmöglichkeiten unterscheiden. Ein Beispiel hierfür ist Wasser. Im (flüssigen) Wasser bilden sich ständig kleine Gruppen (“Cluster” genannt) von Molekülen, die eine Weile zusammenhalten und sich dann wieder lösen. (Weil diese Cluster eine Weile halten, hat Wasser tatsächlich ein “Gedächtnis” für seine Struktur – allerdings müsst ihr eure homöopathischen Mittelchen, die darauf beruhen, seeeehr schnell einnehmen, denn das Gedächtnis hält nur so etwa 0,0000000000001 Sekunde – vielleicht auch eine Null mehr oder weniger…)
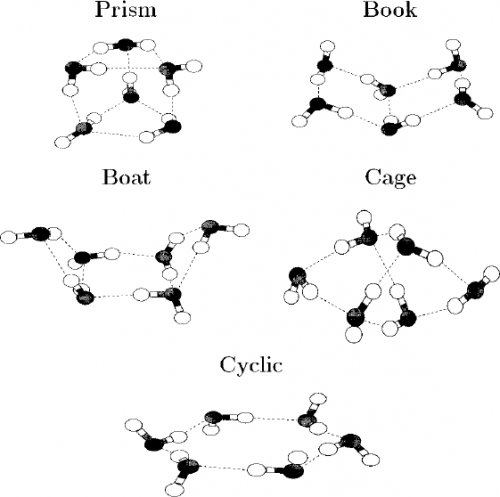
Cluster können unterschiedliche viele Wassermoleküle enthalten. Hier einmal ein paar mögliche Strukturen für Sechser-Cluster (aus dem paper von Gregory/Clary):
Die Cluster haben dabei hübsche Namen, die grob die Form wiedergeben sollen. Berechnet man die Energien der Strukturen, dann ist zunächst die “Prisma”-Struktur (prism) die mit der absolut kleinsten Energie, gefolgt von der “Käfig”-Struktur (cage). Das Ergebnis ändert sich allerdings, wenn man die Nullpunktsenergie berücksichtigt, dann wird tatsächlich die Käfig-Struktur geringfügig günstiger. Auch hier ist also die Nullpunktsenergie wichtig, um die Eigenschaften des Moleküls genau zu verstehen.
Die Nullpunktsenergie ist also nicht nur einfach ein “buchhalterisches” Problem, das sich durch die Wahl des Energie-Nullpunkts quasi von selbst erledigt, sondern sie hat – zumindest in der Quantenmechanik – klar messbare Auswirkungen.
In der Quantenfeldtheorie – also der Quantentheorie der Elementarteilchen – hat auch das Vakuum eine Nullpunktsenergie, weil man Teilchen im Vakuum als “Schwingungsanregungen” betrachten kann, ganz ähnlich (zumindest mathematisch) wie die Schwingungen unserer Moleküle. Die physikalische Bedeutung dieser Nullpunktsenergie ist allerdings deutlich unklarer – berechnet man, wie groß sie etwa sein sollte, kommen gigantische Werte heraus, die so hoch sind, dass das Universum eigentlich sofort aufgrund dieser Energie und der daraus resultierenden Schwerkraft kollabieren sollte. Da es das nicht tut, haben wir da wohl irgend etwas noch nicht verstanden. Die Beispiele aus der Quantenmechanik zeigen aber zumindest, warum man in der Physik die Nullpunktsenergie nicht einfach unter den Teppich kehren sollte – wenn sie dort relevant ist und messbare Konsequenzen hat, warum sollte das in der Quantenfeldtheorie anders sein?
Die Relevanz der Nullpunktsenergie für atomistische Berechnungen ist mir gerade in diesem Buch begegnet:
Sholl, David, and Janice A. Steckel. Density functional theory: a practical introduction. John Wiley & Sons, 2011.
Die Berechnungen zum Zinkoxid findet ihr in
Chris G. Van de Walle, Hydrogen as a Cause of Doping in Zinc Oxide, Phys Rev Lett, 85 (2000), 1012
Und die Cluster im Wasser stammen aus
Gregory&Clary, Structure of Water Clusters. The Contribution of Many-Body Forces, Monomer Relaxation, and Vibrational Zero-Point Energy, J. Phys. Chem. 1996, 100, 18014-18022






Kommentare (34)