Edelgase bestehen aus Atomen, die sich normalerweise nicht chemisch binden, weil sie eine günstige Anordnung ihrer Elektronen haben (eine “volle Elektronenschale”), die chemische Bindungen energetisch wenig attraktiv machen. (Traktiert man sie mit hinreichend fiesen Reaktionspartnern, können sich aber einige Edelgase wie Xenon doch chemisch verbinden, aber das sind exotische Ausnahmen.) Edelgase haben also eigentlich keine Anziehungskräfte mit anderen Atomen und Molekülen. Trotzdem werden sie flüssig und schließlich (mit Ausnahme von Helium) fest, wenn man sie abkühlt. Auch andere chemisch gesättigte Moleküle bilden irgendwann Flüssigkeiten und Festkörper. Wieso eigentlich? Diese Anziehungskraft beruht auf rein quantenmechanischen Effekten, wird aber gern verwirrend dargestellt.
Schauen wir erst einmal auf die “handelsübliche” Erklärung dieser so genannten van-der-Waals-Kräfte, die zwar die Grundidee richtig darstellt (anders als es einst ein gewisser Chemie-Lehrer tat, der im Chemie-Leistungskurs ernsthaft behauptete, die van-der-Waals-Wechselwirkung beruhe auf Gravitation…), aber leider ein paar Grundlagen der Quantenmechanik ignoriert. Und da ich gerade merke, dass ich gleich einen Schreibkrampf bekomme, kürze ich ab sofort die Wechselwirkung mit vdW-Wewi oder vdW-Kraft ab (und bei meinem momentanen Talent für Tpipfehler werde ich das mit der Groß- und Kleinschreibung auch nicht immer korrekt machen, fürchte ich,). Anmerkung: Ich spreche hier pauschal von vdW-Kräften – man kann auch etwas genauer sein und unterschiedliche Aspekte unterscheiden, dann müsste man von der Londonschen Dispersionswechselwirkung sprechen oder von der vdW-Wewi im engeren Sinne. Details dazu erklärt euch der Quell allen Wissens.
Ein Atom besteht ja aus einem schweren geladenen Kern und einer Elektronenhülle. Im halb-klassische Bohrmodell kreisen die Elektronen wie kleine Planeten um den Atomkern, aber dieses Bild ist zwar anschaulich nett, aber letztlich falsch. Laut Quantenmechanik muss man die Elektronen über ihre Wahrscheinlichkeit beschreiben, sich an einem bestimmten Ort aufzuhalten (wenn ihr mehr über die Grundlagen der Qm lesen wollt, dann klickt rechts bei Artikelserien, da findet ihr ziemlich viel zum Thema…). Man kann sich die Elektronen also als eine Art “Wolke” vorstellen, die das Atom umgibt, so wie in diesem Bild hier (aus einem Buch, das ich sehr empfehlen kann, muhaha):
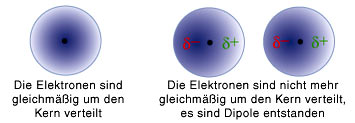
Da das Elektron sich irgendwo in der Wolke aufhält, kann man sich vorstellen, dass es mal am einen und mal am anderen Ort ist – die Wolke soll ja die Wahrscheinlichkeitsverteilung angeben. Und wenn das so ist, dann kann man sich wiederum vorstellen, dass das Elektron mal auf eher der einen Seite des Kerns sitzt und mal eher auf der anderen.
Hat man jetzt zwei Atome nebeneinander, dann sind in jedem dieser beiden Atome die Elektronen in ihren Wolken verteilt. Und wenn man diese Atome jetzt aneinander annhähert, dann ist es energetisch günstig, wenn die Elektronen sich so anordnen, dass das eine Elektron zwischen den beiden Atomkernen ist, das andere aber nicht, so wie in diesem Bild hier:
(Bild von der FU Berlin, Urheberin Mirjam Brockmann, CC License 4.0, wenn ich diesen Hinweis richtig verstehe)
Hier sehen wir, wie sich das Elektron bei beiden Atomen eher etwas weiter links aufhält. Weil der Atomkern positiv geladen ist, ist bei jedem der eigentlich ja elektrisch neutralen Atome die Ladung so verschoben, dass auf der linken Seite etwas mehr negative und auf der rechten Seite etwas mehr positive Ladung zu finden ist. Jedes der Atome bildet damit einen sogenannten elektrischen Dipol. Diese beiden Dipole ziehen sich dann an (weil sich positive und negative Ladung anziehen) und sorgen so für die Kraft zwischen den Atomen.
Nur damit hier keine Missverständnisse aufkommen: Ich mache niemandem einen Vorwurf, der diese Erklärung der vdW-Wewi verwendet. Erstens enthält sie viele richtige Elemente, zweitens steht es so fast überall und drittens muss man manchmal Dinge auch vereinfachen – in dem Link der FU geht es zum Beispiel um Kunststoffe, da will man nicht erst nen Semester Quantenmechanik beibringen. Ich habe die Erklärung auch selbst (allerdings mit dem Hinweis, dass sie vereinfacht ist) verwendet. Hier geht’s nicht darum, dass ich mich über Leute aufregen will, die vereinfachte Erklärungen verwenden, weil das gerade didaktisch sinnvoll ist – aber es schadet ja nix, mal etwas genauer hinzusehen.
Soweit die übliche Erklärung. Sobald man aber etwas darüber nachdenkt und ein paar Grundlagen der Quantenmechanik (QM) berücksichtigt, lässt sie einen ratlos zurück: Die QM sagt uns, dass die Wahrscheinlichkeitsverteilung der Elektronen in einem System, das sich im energetisch günstigsten Zustand befindet, zeitlich unveränderlich ist. Das ist eine Form der berühmten Unschärfe-Relation, nach der es eine (allerdings gern missverstandene) Energie-Zeit-Unschärfe gibt. Ist die Energie genau bestimmt (und das ist sie im Zustand minimaler Energie), dann ist die “Zeitunschärfe” unendlich, oder anders gesagt, der Zustand kann sich mit der Zeit nicht ändern. Ein System mit minimaler Energie ist also absolut stationär, da sich die Wahrscheinlichkeit, das Elektron irgendwo zu finden, zeitlich nicht ändern.
Tja, wenn das aber so ist, dann passt die anschauliche Erklärung der vdW-Wewi nicht mehr so richtig gut, oder? Auch wenn man da natürlich annimmt, dass das System im zeitlichen Mittel stabil ist, braucht man ja doch die momentane Ladungsverteilung, damit die Kraft entsteht. (Ich hoffe, hier ist niemand verwirrt, weil ich mal über Kräfte und mal über Energien rede: Wenn zwei Objekte sich mit einer Kraft anziehen, dann verringert sich ihre Energie, wenn sie sich näherkommen. Deswegen kann man über Wechselwirkungs-Energien oder über Kräfte reden, je nachdem, was gerade passt. Nachher werden wir deshalb die Energie angucken, wenn die beiden Atome, die wir binden wollen, einen bestimmten Abstand haben – wenn diese Energie kleiner wird, wenn wir den Abstand verringern, dann ist die Kraft anziehend.) Und ohne diese momentane Ladungsverteilung klappt die Erklärung mit der vdW-Kraft leider nicht. Entweder der Zustand ist stationär, dann ist aber die Ladungsverteilung symmetrisch und es gibt kein momentanes Ungleichgewicht, oder er ist eben nicht stationär – aber dann ist es kein stabiler gebundener Zustand (und das sollte er sein, wenn zwei Atome oder Moleküle aneinander gebunden sind).
Um zu sehen, was hier tatsächlich passiert, basteln wir uns ein einfaches Modell (das ich diesem Artikel entnommen habe), zunächst mal für ein einzelnes Atom. Wir nehmen an, dass das Atom ein einzelnes Elektron hat, das an den Atomkern gebunden ist und das für die vdW-Wewi verantwortlich ist. (Das Atom muss also nicht unbedingt ein Wasserstoff-Atom sein, wir betrachten der Einfachheit halber eben nur eins der Elektronen.) Um die Sache noch weiter zu vereinfachen, nehmen wir außerdem an, dass die Welt eindimensional ist, unser Elektron kann sich also irgendwo entlang einer Linie aufhalten, aber sonst nichts.
Als letztes nehmen wir noch an, dass die Wechselwirkung zwischen Elektron und Atomkern nicht die normale elektrostatische Anziehung ist, sondern dass wir sie über ein sehr einfache Kraftgesetz beschreiben können, bei dem die Kraft proportional zum Abstand des Elektrons vom Kern ist, so wie bei einer Feder. Je stärker man dehnt, desto größer die Kraft. Die Kraft ist also gleich Null, wenn sich das Elektron genau beim Kern aufhält und nimmt dann nach außen hin immer weiter zu. (Warum machen wir diese ganzen vereinfachenden Annahmen? Weil man dann die Lösung des Problems am Ende relativ leicht berechnen und auch interpretieren kann – ich führe die Rechnung hier nicht vor, weil die in dem zitierten Artikel drin ist und so etwas für Nicht-PhysikerInnen ja immer eher abschreckend wirkt. Außerdem ist die Interpretation eh interessanter als die Rechnung selbst.)
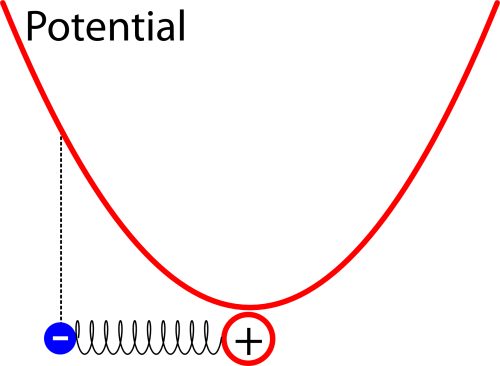
Ein solches System nennt man einen harmonischen Oszillator. Betrachtet man ihn zuerst mit den Mitteln der klassischen Physik, dann nimmt die Energie des Elektrons nimmt nach außen hin quadratisch zu, wenn man sie graphisch darstellt hat sie also die Form einer Parabel. (Dass das so sein muss, davon könnt ihr euch mit den Mitteln der Schulphysik leicht überzeugen: Arbeit ist Kraft mal weg. Wenn ich also das Elektron immer weiter entferne, lege ich zum einen einen immer größeren Weg zurück, zum anderen steigt aber auch die Kraft proportional zum Weg.) Die Energie, die das Elektron an einem bestimmten Ort nach den regeln der klassischen Physik hätte, nennen wir das Potential:
Anmerkung: Es mag auf den ersten Blick verwirrend sein, dass wir die Regeln der klassischen Physik nehmen, um das Potential zu bestimmen, um dann hinterher Quantenmechanik zu betreiben – zumal in der Quantenmechanik ein Elektron, das einen ganz bestimmten Abstand zum Atomkern hat, ja gar keine eindeutige Energie besitzt. So sind aber die Spielregeln: In die Schrödingergleichung (siehe die Artikelserien) geht das Potential ein, also die Energie, die ein klassisches Elektron, das ein Punktteilchen wäre, an einem bestimmten Ort hätte. Alternativ kann man sich das vielleicht auch mit dem Pfadintegral verstehen (zu dem sage ich unten eh noch etwas): Darin betrachtet man alle denkbaren Wege, die ein Elektron als punktteilchen gehen könnte, und überlagert die dann in bestimmter Weise, um das Endergebnis auszurechnen. Also nicht verwirren lassen: Wenn ich von der Energie (oder dem Potential) an einem punkt spreche, dann ist die “klassische” Energie gemeint – ein echtes quantenmechanisches Elektron dagegen, das eine bestimmte Energie hat, sitzt nie an einem einzigen Punkt, sondern hat eine über den Raum passend verteilte Aufenthaltswahrscheinlichkeit. (Falls euch das immer noch verwirrt, dann hinterlast bitte einen Kommentar – das gilt generell für diesen Artikel, ich habe keine Ahnung, ob der für nicht Physikerinnen verständlich ist, also bitte im Zweifel unten beschweren.)
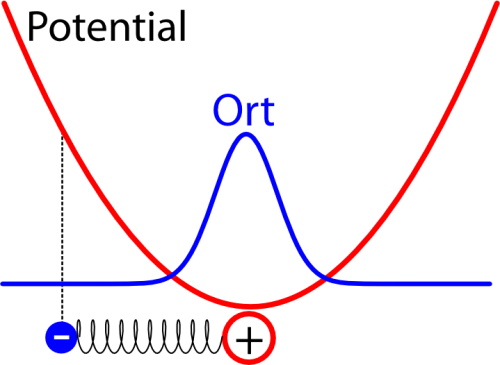
Wie der harmonische Oszillator quantenmechanisch funktioniert, habe ich neulich schon mal ausführlich erklärt, also folgt hier nur die Kurzfassung. Man kann dieses Problem relativ leicht lösen – im Zustand mit der niedrigsten Energie kommt heraus, dass das Elektron die größte Wahrscheinlichkeit dicht am Atomkern hat, aber auch in einem gewissen Abstand zum Kern gefunden werden kann. So etwa sieht die Verteilung für den Ort des Elektrons aus, wenn man sie in das Potential einzeichnet (das schematisch eingezeichnete Elektron hat dabei eigentlich keine Bedeutung mehr und soll euch nur erinnern, dass wir es mit einem Oszillator zu tun haben):
Die Breite der Verteilung hängt dabei davon ab, wie stark das Elektron an das Atom gebunden ist (also davon, wie steil die Parabel für das Potential ist) – je stärker die Bindung ist, desto schmaler ist die Verteilung und desto höher ist die Energie des Elektrons. (Dass die Energie bei stärkerer Bindung höher wird, mag verwirrend erscheinen, lässt sich aber wie folgt erklären: Wir haben den Energie-Nullpunkt ungewöhnlich gewählt, normalerweise wählt man ihn so, dass die Energie des ungebundenen Elektrons verschwindet, aber das geht hier nicht, weil die Energie mit zunehmender Entfernung immer größer wird. Man kann sich dann mit Hilfe der Unschärferelation anschaulich machen, dass ein Elektron, das auf einen schmaleren Bereich begrenzt ist und dessen Ort deswegen genauer bekannt ist, eine größere Unschärfe im Impuls haben muss, so dass die Energie größer ist.)
Also: Das Elektron hat eine Aufenthaltswahrscheinlichkeit um den Atomkern herum. Diese ist zeitlich vollkommen konstant (der Zustand hat eine eindeutige Energie und ist deswegen stationär). Messen könnt ihr diese Verteilung nur statistisch, wenn ihr sehr viele solcher Atome untersucht und den Ort des Elektrons bestimmt; dann kommt am Ende eben diese Verteilung heraus. (Ja, das ist verwirrend – aber das liegt nicht an meiner Erklärung (oder jedenfalls nicht nur) sondern einfach daran, dass die QM nun mal verwirrend ist – rechts bei den Artikelserien könnt ihr Details zu diesem Problem in den verschiedenen Artikeln nachlesen.)
Als nächstes – eigentlich geht es in diesem Artikel um die vdW-Wewi, erinnert sich noch jemand? – nehmen wir noch ein zweites identisches Atom hinzu, das wir – in einigermaßen großer Entfernung – rechts vom ersten Atom platzieren, etwa so (ich vereinfache das Bild jetzt etwas…):
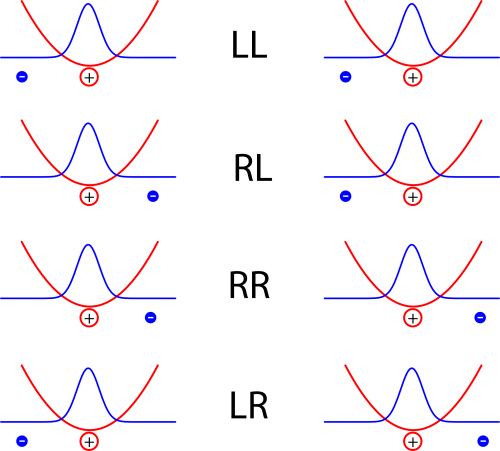
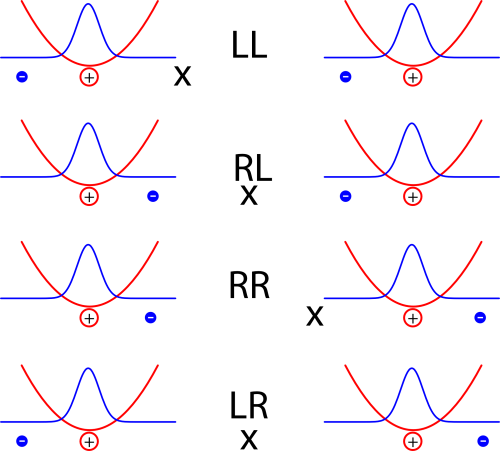
Diese beiden Atome (eigentlich sollte ich wohl, weil das Modell so extrem vereinfacht ist, “Atome” in Anführungsstiche setzen, aber das spare ich mir aus Faulheit) – also diese beiden Atome wechselwirken jetzt miteinander. Um zu sehen, wie sie das tun, nehmen wir mal kurz an, die Elektronen wären jeweils an einem Ort lokalisiert und schauen auf verschiedene Möglichkeiten:
Die vier Kürzel stehen dabei für die lage der Elektronen, rechts oder links vom jeweiligen Kern
Jedes der Atome bildet hier im Bild einen Dipol, und die Energie ist natürlich dann kleiner, wenn sich positive und negative Ladungen abwechseln als wenn in der Mitte zwei positive oder zwei negative Ladungen aufeinandertreffen. Die Anordnungen LL und RR sind also energetisch günstig, LR oder RL dagegen eher ungünstig. (Warnung: Auf den ersten Blick mag das Konstrukt hier sehr an die Beschreibung des Wasserstoff-Moleküls aus diesem Artikel erinnern, wo aber ein ganz anderes Ergebnis herauskam. Der Grund ist der, dass im Modell hier die beiden Atome so weit voneinander entfernt sind, dass wir annehmen, dass es zum einen keinen Unterschied in der Energie zwischen der Anordnung LR und der Anordnung RL gibt, und dass zum anderen die Aufenthaltswahrscheinlichkeit der Elektronen in der Mitte zwischen den Atomen verschwindend klein ist.)
Falls ihr gerade verwirrt seid, dass ich erst die Elektronen mit ihrer Aufenthaltswahrscheinlichkeit beschreibe und jetzt doch wieder klassische Bildchen male: Um die Energie eines Elektrons (mit Hilfe der Schrödinger-Gleichung) zu berechnen, braucht man ja (siehe oben) das Potential, also die Energie als Funktion des Ortes für jeden Ort, die das Elektron hätte, wenn es ein klassisches Teilchen wäre – daraus kann man dann die Aufenthaltswahrscheinlichkeit berechnen.
Wir haben jetzt ein auf den ersten Blick kniffliges Problem, weil die Energien der beiden Elektronen sich gegenseitig beeinflussen. Nach den Regeln der QM passiert jetzt etwas ziemlich kompliziertes: Es gibt nicht mehr eine Aufenthaltswahrscheinlichkeit für das eine Elektron und eine zweite für das andere Elektron, sondern die beiden Wahrscheinlichkeiten sind korreliert: Die Wahrscheinlichkeit, das linke Elektron am Ort x zu finden, hängt davon ab, wo das rechte Elektron sitzt. (Mathematisch äußert sich das so, dass wir die Funktion betrachten müssen, wobei sich die nicht einfach als Produkt zweier Funktionen
schreiben lässt.)
Als nächstes überlegt man sich folgendes: Die Energie zwischen den beiden Atomen hängt ja davon ab, ob die Elektronen auf derselben Seite ihres jeweiligen Atoms sitzen oder nicht. Sitzen sie beide in der Mitte, also in der Anordnung RL (dann ist ihr Abstand besonders klein), ist das energetisch ungünstig, sitzen sie beiden an ihrem Atom “außen” (in der Anordnung LR), dann ist das energetisch auch schlecht. Aber wie bei Goldlöckchen und den drei Bären gibt es auch hier einen Abstand, der genau richtig ist – wenn nämlich die beiden Elektronen genau so weit voneinander entfernt sind wie die beiden Atomkerne, so wie bei den Bildern LL und RR. Deshalb ist es praktisch, wenn wir nicht die Orte der Elektronen selbst betrachten, sondern den Abstand zwischen ihnen nehmen, um das Problem zu beschreiben.
Es reicht aber natürlich nicht, den Abstand der beiden Elektronen zu kennen, um zu wissen, wo sie sind (ich brauche zwei Zahlen, für jedes Elektron eins). Zusätzlich können wir noch den Mittelpunkt (oder Schwerpunkt) zwischen den beiden Elektronen betrachten. Sitzt der genau in der Mitte zwischen den Atomen, dann ist die Anordnung der Elektronen spiegelsymmetrisch; ansonsten sind die Elektronen nach links oder rechts verschoben. Ich habe die Schwerpunkte mal mit einem x gekennzeichnet (es wurde zwar noch nie in der Geschichte der Archäologie ein Schatz bei einem “x” gefunden, aber gegen einen Schwerpunkt spricht hoffentlich nichts):
Statt das Potential also über die beiden Orte der Elektronen zu beschreiben, beschreiben wir es über den Abstand und die Lage des Schwerpunkts. Und wenn man das tut, dann zeigt sich der Nutzen unseres extrem vereinfachten Modells mit dem simplen Federgesetz: Die vorher komplizierte Gleichung zerfällt (jedenfalls für hinreichend große Atomabstände) sauber in zwei Teile. Es gibt eine Gleichung für die Lage des Schwerpunkts, eine zweite für den Abstand. Und jede dieser Gleichungen sieht genau so aus wie die Gleichung eines harmonischen Oszillators. Damit sind dann auch die Lösungen dieselben wie für den Oszillator.
Der Schwerpunkt der beiden Elektronen ist also im Mittel so verteilt (die schwarze Kurve):
Am wahrscheinlichsten ist eine Lage in der Mitte, aber auch rechts und links von der Mitte mag sich der Schwerpunkt aufhalten.
Und der Abstand der beiden Elektronen hat diese Verteilung (das ist jetzt etwas schwierig zu zeichnen – das Bild ist so gemeint, dass ich den Nullpunkt des Abstandes immer beim linken Elektron habe; dann der Abstand zwischen den beiden Elektronen am wahrscheinlichsten, der genau dem Atomabstand entspricht. Ich hoffe, man kann das irgendwie verstehen):
Schaut man sich die Verteilungen genauer an, so stellt man fest, dass die Breite der Verteilung für die Schwerpunktslage etwas größer ist als die ursprüngliche Breite der Verteilung für eins der beiden Elektronen. Umgekehrt ist die Breite der Verteilung des Abstands etwas schmaler. Das ist auch plausibel, denn wir haben ja gesehen, dass es eben energetisch besonders günstig ist, wenn die beiden Elektronen den richtigen Goldlöckchen-Abstand haben. Umgekehrt ist es dann aber eben wahrscheinlicher, beide Elektronen links oder rechts von ihrem Atom zu finden, so dass die Breite der Verteilung für den Schwerpunkt größer ist.
In der Summe stellt sich heraus (weil die Breite der Verteilung ja etwas mit der Energie zu tun hat), dass man insgesamt durch die Wechselwirkung etwas Energie gewinnt – es ist energetisch günstiger, wenn die beiden Atome in dieser Weise wechselwirken, als wenn sie es nicht tun. Und je kleiner der Abstand der Atome ist, desto größer ist der Energiegewinn. Es ist also energetisch günstig, wenn sich die Atome annähern – mit anderen Worten: Sie ziehen sich an. Und das ist genau die vdW-WeWi.
Insofern klingt das wieder sehr ähnlich zu der Erklärung, die ich am Anfang vorgestellt habe. Aber tatsächlich ist der Zustand der Elektronen eben nicht einfach so, wie im Bild ganz oben dargestellt, so dass die Elektronen mal links und mal rechts vom Atomkern sind, sondern der Zustand ist eine Überlagerung aus solchen Bildern. Deshalb kann er auch vollkommen zeitunabhängig sein, und trotzdem ist die Wahrscheinlichkeit größer, beide Elektronen jeweils entweder rechts oder links von ihrem Atomkern zu finden.
Interessanterweise taucht diese Verwechslung zwischen dem “momentanen” (und letztlich falschen) Bild und dem tatsächlichen quantenmechanischen Bild sogar in dem zitierten Artikel auf. Dort steht: “there is a shift [of the energy] … since at any given instant of time there exists an instantaneous dipole moment in, say, atom #1. ” [Es gibt eine Verschiebung [der Energie] … weil es in jedem Moment ein momentanes Dipolmoment in beispielsweise Atom #1 gibt.] Was wieder einmal zeigt, dass auch PhysikerInnen sich gern mal etwas falsche Anschauungen basteln.
Man kann sich das ganze auch im Pfadintegral-Bild anschaulich machen (das ich ausführlich in diesem Artikel erklärt habe). Danach kann man das Verhalten von Elektronen dadurch beschreiben, dass man alle denkbaren Möglichkeiten für das, was die Elektronen tun können, aufschreibt und für jede dieser Möglichkeiten dann eine Zahl berechnet. Alle diese Zahlen aufaddiert erlauben es dann, die Wahrscheinlichkeit für einen bestimmten Prozess zu berechnen. (In dem verlinkten Artikel wird das genauer erklärt.)
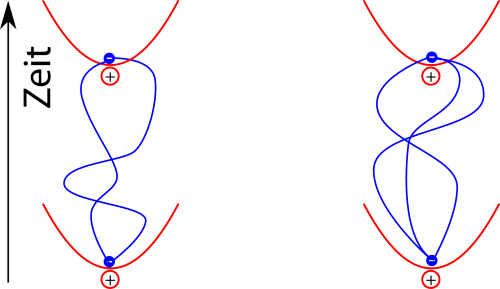
Für die vdW-Wewi heißt das jetzt, dass wir zum Beispiel alle Möglichkeiten angucken können, wie zwei Elektronen, die am Anfang genau in der Mitte sitzen, das nach einem bestimmten Zeitraum wieder tun. (Der genaue mathematische Formalismus ist hier ziemlich fies, aber die Idee ist zum Glück einfach):
Berücksichtigt man jetzt die Wechselwirkung der elektrischen Dipole in jeder dieser Situationen, dann sieht man, dass man die beiden Elektronen nicht isoliert betrachten kann, sondern dass die Pfade sich gegenseitig beeinflussen. Pfade der Elektronen wie in diesem Bild hier
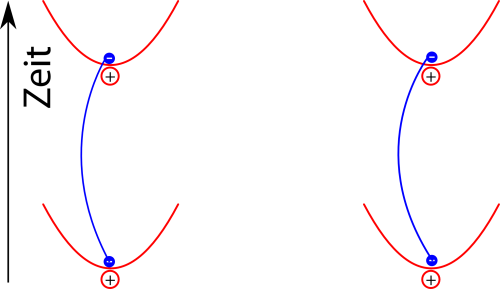
leisten dann wegen der Energieersparnis einen größeren Beitrag zum Endergebnis als zum Beispiel dieser:
Auch in diesem Bild ist es wichtig, dass man die Pfade der Elektronen gemeinsam betrachtet: Die Wahrscheinlichkeit für die unterschiedlichen Pfade des linken und des rechten Elektrons sind gekoppelt, und genau das führt dann am Ende dazu, dass die Energie des Systems sich verringert.
In diesem Bild kann man übrigens auch berücksichtigen, dass sich die beiden Elektronen (bzw. die Dipole) über ein elektrisches Feld beeinflussen, das man sich wiederum als aus Photonen bestehend vorstellen kann. Diese komplexere Betrachtung wird in dem zitierten Paper (s.u.) auch angesprochen (tatsächlich macht sie den Großteil aus, während das, was ich hier vorgeführt habe, auf nicht mal eine Seite passt…), aber ich gebe zu, dass ich mir diesen Aspekt nicht so genau angesehen habe.
Egal welches Bild ihr betrachtet: Die vdW-Wewi beruht darauf, dass die Energie der beiden Elektronen vom relativen Ort der beiden abhängt. Diese Korrelation hat auch dann einen Einfluss, wenn man berücksichtigt, dass der gesamte quantenmechanische Zustand vollkommen zeitunabhängig ist – trotzdem können die Orte der Elektronen sich beeinflussen. Dass auch Edelgase irgendwann flüssig und fest werden, verdanken wir nur diesen Korrelationen. Wieder einmal ein schönes – wenn auch etwas kompliziertes – Beispiel für die seltsamen Verwicklungen in der Quantenwelt.
Holstein, Barry R. “The van der Waals interaction.” American Journal of Physics 69.4 (2001): 441-449.










Kommentare (66)