Die kürzeste Verbindung zwischen zwei Punkten ist bekanntlich eine Gerade – das habt ihr vermutlich mal in der Schule gelernt. In der handelsüblichen Geometrie ist das auch richtig – aber nicht in der Physik. Denn Massen krümmen laut der Allgemeinen Relativitätstheorie (ART) den Raum. Heute schauen wir ein bisschen, was das bedeutet und warum der kürzeste Weg zwischen zwei Punkten auch davon abhängt, wie schnell man unterwegs ist.
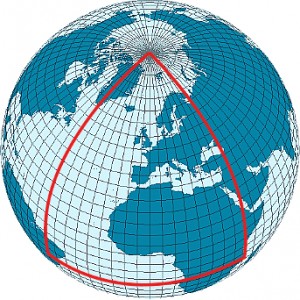
Die ART sagt ja bekanntlich aus, dass die Raumzeit gekrümmt ist (was das bedeutet, habe ich vor ein paar Jahren ja schon einmal ausführlich erklärt – und wenn ich meinen alten Text genauer gelesen hätte, hätte ich mir viel Verwirrung sparen können…). Schauen wir uns zunächst einmal die Krümmung des Raums an. Die wird gern mit der Analogie zu einer gekrümmten Fläche – beispielsweise einer Kugeloberfläche erklärt. Dieses Bild hier zeigt beispielsweise, dass auf einer gekrümmten Fläche die Winkelsumme im Dreieck größer als 180° sein kann:
Leider führen diese Veranschaulichungen leicht dazu, dass man sich einen “Hyperraum” vorstellt, in den der gerade betrachtete Raum eingebettet ist – wenn sich der Raum krümmt, dann muss er sich ja scheinbar in irgendetwas krümmen. Dass das nicht so sein muss, habe ich seinerzeit mit Hilfe von Landkarten zu erklären versucht.
Eine andere Erklärung dafür, wie ein Raum gekrümmt sein kann, ohne dass man ihn in einen Hyperraum einbetten muss, wurde durch die Feynman Lectures populär (die Idee ist aber nicht von Feynman und geht ursprünglich wohl auf Poincare zurück – hinter dem Link verbirgt sich übrigens eine extrem ausführliche Internetseite über Einstein und die RT, die extrem zu empfehlen ist). Dazu stellt man sich eine kreisförmige Platte vor, bei der sich die Temperatur von Ort zu Ort ändert, etwa so (ich würde ja direkt das niedliche Bild aus den Feynman lectures nehmen, aber die Seite macht ziemlich klar, dass das nicht so gern gesehen ist):
Die Platte ist hier im Bild Außen heißer als Innen, aber man kann sich natürlich auch kompliziertere Temperaturverteilungen vorstellen.
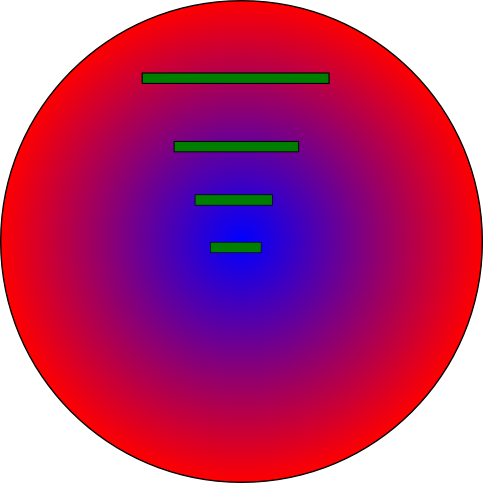
Wir stellen uns jetzt Lebewesen vor, die auf dieser Platte leben (Feynman nennt sie einfach “bugs” und zeichnet niedliche Krabbelkäfer). Bekanntlich dehnen sich Materialien ja aus, wen sie warm werden, so dass ein Maßstab an unterschiedlichen Stellen der Platte unterschiedlich lang ist. Wir nehmen jetzt an, dass diese Ausdehnung für alle Materialien in unserer Plattenwelt gleich groß ist – die Käfer, ihre Maßstäbe, ihre Autos und alles andere dehnen sich bei einer Temperaturänderung um exakt den selben Faktor. So etwa sieht es aus, wenn wir einen einheitlichen Maßstab an verschiedene Stellen legen (ich bin etwas ungenau beim Zeichnen, weil die Temperatur über den Maßstab ja nicht ganz homogen ist; stellt euch einfach vor, der Maßstab liegt an einem Punkt und ist hier nur deutlich vergrößert gezeichnet, damit man etwas sieht.)
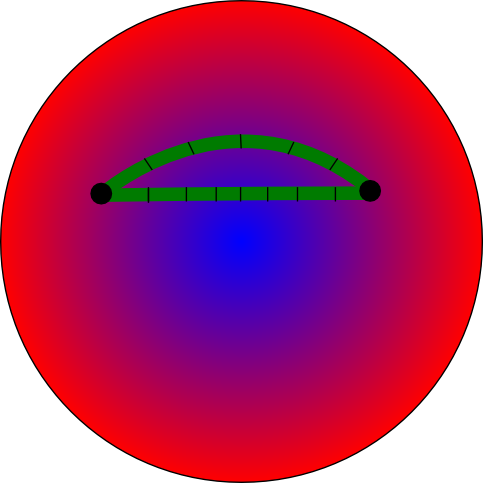
Wenn unsere Käfer den kürzesten Abstand zwischen zwei Punkten messen wollen, dann können sie das dadurch tun, dass sie auf unterschiedlichen Wegen von A nach B gehen und die Strecke mit ihren Maßstäben messen. Der kürzeste Weg ist dann der, bei dem sie die kleinste Zahl von Maßeinheiten brauchen. Weil die Maßstäbe nach Außen hin länger werden, ist der kürzeste Weg von A nach B gekrümmt, etwa so:
Der untere Weg ist länger, denn die Maßstäbe sind dort kürzer. (Für uns sieht die Sache von Außen anders aus, weil unsere Maßstäbe nicht mitschrumpfen.)
Alternativ können die Käfer auch die Punkte A und B mit einem Stahlseil verbinden, das sie so straff ziehen, wie es nur geht – das Seil legt sich dann natürlich so, dass es die kleinste Länge hat. (Diese Analogie ist nur eine Näherung – in einem Schwerefeld hängt ein Seil natürlich immer ein wenig durch. Falls ihr euch fragt, wie man das Durchhängen im Bild der Raumkrümmung beschreibt: Die festgehaltenen Enden des Stahlseils werden in diesem Bild ständig beschleunigt, weil das Seil eigentlich frei fallen “will”.)







Kommentare (61)