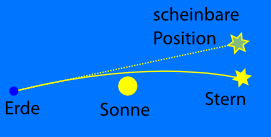
Und hier kommt schon die kleine Denkfalle: Vermutlich haben viele von Euch schon mal gehört, dass sich Licht um eine Masse herum krümmt, also gebogene Wege läuft. Meist sieht man dazu Bilder wie dieses hier:
Und wenn man jetzt diese beiden Bilder vergleicht, dann kann man auf den naheliegenden Gedanken kommen, dass die Krümmung des Raumes genau so funktioniert wie bei der heißen Platte und dass Licht deswegen so abgelenkt wird. Das ist auch nicht völlig falsch – aber es ist auch nicht so ganz richtig. In Wahrheit ist die Sache (wie so oft) etwas komplizierter.
Um das zu sehen, schauen wir erst einmal, ob unsere kleinen Krabbelkäfer eigentlich herausfinden können, dass ihre Platte sich so seltsam verhält. Wenn sie einfach nur herumlaufen oder Strecken messen, sehen sie ja nichts von der Krümmung, die ist nur für uns von Außen deutlich zu erkennen.
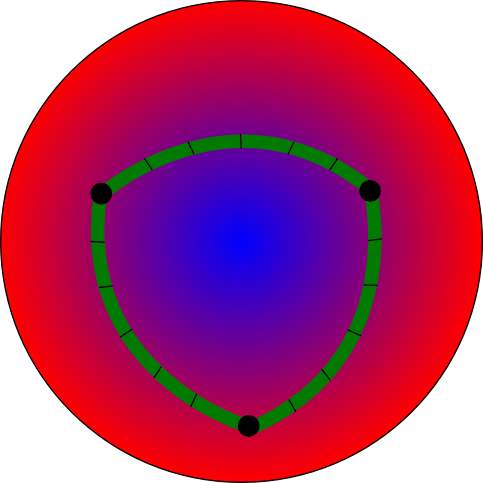
Aber unsere Krabbelkäfer können leicht herausfinden, dass ihre Platte sich etwas eigenwillig verhält. Eine Möglichkeit dazu sind Dreiecke. Bekanntlich ist die Winkelsumme im Dreieck 180°; wenn unsere Käfer sehr kleine Dreiecke zeichnen (so dass die Ausdehnung ihrer Maßstäbe beliebig klein wird), dann können sie das auch genau so herausfinden, wie wir das können. Wenn sie jetz aber ein großes Dreieck zeichnen, dann erleben sie eine Überraschung – die Winkelsumme im Dreieck ist nämlich größer als 180°:
Daraus können die Käfer schließen, dass ihre Welt so gekrümmt ist wie eine Kugeloberfläche.
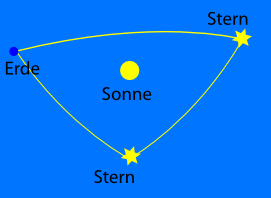
Wir können genau so ein Dreieck in unserem Universum zeichnen, wenn wir noch einen zweiten Stern zur Verfügung haben:
Auch hier ist die Winkelsumme größer als 180° (das muss so sein, weil die Sterne ja scheinbar von der Sonne nach Außen verschoben werden). Die Raumzeit um die Sonne herum ist also genau so gekrümmt, wie bei der heißen Platte, oder?
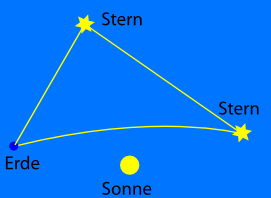
Nein, ist sie nicht. Um das zu sehen, betrachten wir ein anderes Dreieck:
Der zweite Stern oben ist jetzt so weit von der Sonne weg, dass sein Licht (fast) nicht beeinflusst wird, entsprechend habe ich zwei Seiten des Dreiecks gerade gemalt. Wenn ihr jetzt die Winkelsumme ausmesst, ist sie kleiner als 180°. Eine solche Winkelsumme können wir auf der Platte auch bekommen, wenn wir das Temperaturfeld umdrehen:
Hier sind jetzt Wege Innen kürzer, weil die Maßstäbe nach Innen hin länger werden.
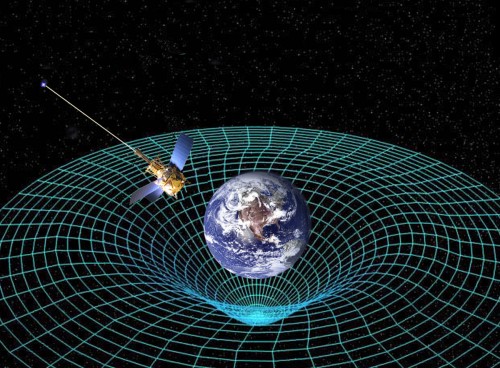
Der Raum um eine Masse herum ist nämlich nicht gleichmäßig gekrümmt. Im Inneren der Masse ist die Krümmung positiv wie bei einer Kugel, Außen ist sie negativ (wie bei einem Sattel). Das sieht man auch auf den üblichen Bildern wie diesen hier, bei denen der Raum als eine Art Gummituch dargestellt wird (wobei bei diesem Bild die Linien von Innen nach Außen nicht gerade verlaufen, vermutlich, weil die Rotation der Erde mit einbezogen wird):
(Bild von der NASA, Public domain)
Ein großes Dreieck, dass die Erde einschließt, hat eine Winkelsumme von mehr als 180°, eins, das das nicht tut, sondern außerhalb liegt, eine Summe von weniger als 180°. Ich habe eine Weile überlegt, wie sich das im Bild der heißen Platte darstellen lässt, bin aber zu keinem sinnvollen Ergebnis gekommen (vielleicht habe ich auch einen Denkpatzer gemacht – falls es doch geht, schreibt bitte einen Kommentar) – ich denke, es liegt daran, dass bei unserer heißen Platte die Längenänderung nicht von der Richtung abhängt, während sie das im gekrümmten Raum tun kann. Trotzdem ist die heiße Platte aber ein nützliches Modell, um zu sehen, wie man Raumkrümmungen darstellen kann, ohne auf “Gummituchmodelle” zurückzugreifen.
Aber auch wenn das Bild der heißen Platte nur bedingt weiterhilft – immerhin haben wir jetzt gesehen, wie die Sonne (oder irgendeine andere Masse) den Raum krümmt, und der gekrümmte Lichtweg ist anscheinend genau analog zu dem gekrümmten Weg, den wir auf der heißen Platte gehen, um den kürzesten Weg zwischen A und B zu finden.







Kommentare (61)