Stellt euch also vor, ihr sucht den kürzesten Weg zwischen dem Stern und der Erde (weil ihr vielleicht eine Hyperraumumgehungsstraße bauen wollt). Der Einfachheit halber nehmen wir an, dass Erde, Sonne und Stern stillstehen, sonst wird es natürlich komplizierter. Nach dem, was wir bisher überlegt haben, könnte man das so machen: Man schickt einen Lichtstrahl vom Stern zur Erde, verfolgt dessen Weg und nimmt das als kürzesten Weg zwischen Erde und Stern. Das klingt vernünftig, und passt auch dazu, dass es in Büchern und Artikeln zur ART gern heißt, dass Licht auf sogenannten Geodäten läuft, die das Äquivalent einer geraden Linie in der gekrümmten Raumzeit sind.
Diese naheliegende Idee ist aber leider falsch. Licht nimmt zwar tatsächlich den kürzesten Weg zwischen zwei Punkten, aber der kürzeste Weg ist nicht der mit der kürzesten Strecke. (Ich habe eben noch so getan, als wäre das so, damit es nicht schon am Anfang zu kompliziert wird.)
Wie jetzt!? Das klingt ja erst Mal etwas absurd und in sich widersprüchlich.
Keine Sorge – da gibt es keine Widersprüche und mit der ART ist alles in Ordnung (naja, angesehen von Problemen mit der Energieerhaltung und Zeitreisen und damit, dass man die ART nicht anständig quantisieren kann – eine supergute Theorie ist sie trotzdem, auch wenn der Name “perfekte Theorie” meiner Ansicht nach nicht so gut passt). Ich war nur etwas schlampig mit meinen Begriffen, genauer gesagt mit dem Begriff “Punkt”.
Ein “Punkt” in der ART ist nicht einfach ein Punkt im Raum – die ART ist eine Theorie der Raum-Zeit. Um einen Punkt in der Raumzeit festzulegen, muss man eben nicht nur sagen, wo man ist, sondern auch, wann man ist. Deswegen spricht man auch gern von “Ereignis”, wenn man einen Punkt in der Raumzeit meint (das Wort steckt auch im “Ereignishorizont” eines Schwarzen Lochs – der heißt nicht so, weil da so viel los ist…).
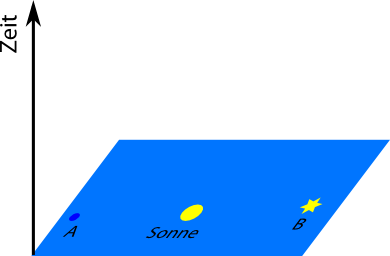
Wenn wir – wie die Krabbelkäfer auf ihrer Platte – die Punkte A und B (also beispielsweise Erde und Stern) mit einem Stahlseil verbinden, dann hängt es zwischen den beiden Raumpunkten A und B rum – und zwar so, dass es zu jedem Zeitpunkt an beiden Enden gleichzeitig befestigt ist, und auch unsere Maßstäbe haben wir einfach hingelegt und liegen gelassen. (Weil “Gleichzeitigkeit” in der RT nicht universell gültig ist, müssen wir uns für ein bestimmtes Bezugssystem entscheiden – am einfachsten das, in dem die Raumpunkte A und B und die Masse dazwischen alle in Ruhe sind.) Betrachten wir (in diesem System) zwei gleichzeitige Raumzeitpunkte – also die Raumpunkte A und B zu einer bestimmten Zeit, beispielsweise 12:00Uhr mittags.
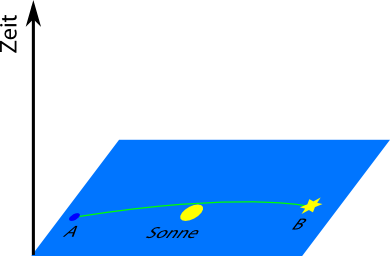
Da die beiden Raumzeitpunkte räumlich voneinander getrennt aber gleichzeitig sind, ist es nicht möglich, ein Signal von einem zum anderen zu schicken. Die höchste mögliche Geschwindigkeit ist ja die Lichtgeschwindigkeit, aber um von A nach B in exakt Null Sekunden zu kommen, bräuchte wir unendlich hohe Geschwindigkeiten, und die gibt es nicht. (Außer vielleicht auf der Hyperraumumgehungsstraße?) Solche Raumzeitpunkte (oder Ereignisse) heißen “raumartig” getrennt. Die kürzeste Verbindung zwischen unseren beiden gleichzeitigen Ereignissen (A und B um 12.00Uhr mittags) ist also die kürzeste Linie im Raum. Da wir gleich auch noch die Zeit einzeichnen müssen, baue ich noch eine Zeitachse ins Bild ein:
Wir zeichnen jetzt die kürzeste Linie im Raum ein, also eine Linie, die wir bekommen, indem wir ein Stahlseil spannen oder indem wir Maßstäbe legen wie es die Käfer gemacht haben. So sieht sie (so in etwa) aus:
Um die Länge dieser Linie zu bestimmen, können wir sie in sehr viele sehr kleine Stückchen zerteilen, so dass jedes Stückchen näherungsweise gerade ist. (Ausführlicher habe ich das und das, was als nächstes kommt, im 4. Teil der Raumzeit-Krümmungs-Serie diskutiert – den ihr übrigens ziemlich unabhängig von den anderen Teilen lesen könnt.) Wenn wir ein Koordinatensystem haben, dann können wir die Länge jedes Stückchens mit dem Satz des Pythagoras berechnen:






Kommentare (61)