Falls ihr euch fragt, warum ich das so umständlich mache – ich könnte ja auch das Stück direkt messen statt seine Achsabschnitte in den beiden Koordinatenrichtungen -, nun, das ist ganz simpel: Gleich werden wir Wege betrachten, die sich durch Raum und Zeit erstrecken, und da können wir nicht so ohne weiteres “schräge” Linien ausmessen.
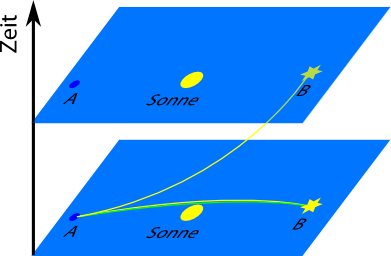
Jetzt senden wir also ein Signal von A nach B, so dass das Signal bei A zu einer bestimmten Zeit startet und zu einer späteren bei B ankommt. (Wenn das ohne Überlichtgeschwindigkeit möglich ist, dann heißt der Abstand zwischen den beiden Punkten zeitartig.) Dafür gibt es verschiedene Möglichkeiten: Wir könnten zum Beispiel Bälle werfen (wenn wir so weit werfen können) oder ein Lichtsignal schicken. Was ist jetzt die kürzeste Verbindung zwischen den beiden Punkten?
Starten wir erst einmal mit dem Lichtsignal. Den Pfad, den das Signal nimmt, kennen wir ja schon (der führte ja gerade zur Lichtablenkung), jetzt kommt nur noch die Zeitachse hinzu. So etwa sieht das aus:
Hier habe ich jetzt eine Strecke in der Raumzeit, die ich ausmessen möchte. Wie man den räumlichen Teil ausmisst, wissen wir schon, aber was ist mit dem zeitlichen Teil? Den zeitlichen Abstand zwischen zwei Punkten messen wir in Sekunden – da die Lichtgeschwindigkeit eine Naturkonstante ist, können wir Sekunden ohne weiteres in Meter umrechnen – eine Sekunde entspricht einer Strecke von 300000 Kilometern (was man auch gern als “Lichtsekunde” bezeichnet, ganz analog zum alten Begriff der “Wegstunde”).
Betrachten wir also ein kleines gerades Wegstück in der Raumzeit. Können wir die räumliche und die zeitliche Strecke ebenfalls mit Hilfe des Satzes des Pythagoras addieren? Nein, das können wir nicht. Raum und Zeit sind ja nicht dasselbe, sondern durchaus unterschiedliche Dinge, und das bleiben sie auch in der ART. Der Satz des Pythagoras bleibt zwar fast erhalten, aber er bekommt ein Minuszeichen: Der raum-zeitliche Abstand berechnet sich nach ds²=dx²-dt² (ich lasse jetzt die Wurzel weg und schreibe ds², sonst gibt es Ärger, wenn die Wurzel negativ wird, damit wollen wir uns jetzt nicht befassen (ich jedenfalls nicht (und zum Glück ist es mein Blog (muhaha))):
Typischerweise ist es in den meisten Büchern dabei die räumliche Komponente, die das Minus-Zeichen bekommt. Ich mache es hier aber andersherum (und damit auch andersherum als in meiner alten Raumkrümmungs-Serie), weil das den Vorteil hat, dass wir nach wie vor von kürzesten Strecken in der Raumzeit reden. Wie lang ist also die Strecke in der Raumzeit, die unser Lichtsignal nimmt?
Da wir Raum und Zeit mit Hilfe der Lichtgeschwindigkeit ineinander umgerechnet haben, legt ein Lichtstrahl in einer Zeit dt genau eine räumliche Strecke dx=c dt zurück. Für den Lichtstrahl ist also der Raumzeitabstand genau gleich Null. Die zugehörige Bahn ist wieder gekrümmt (das wussten wir ja schon von der Lichtablenkung), und zwar stärker als bei unserem kürzesten Weg im Raum. Dass das so sein muss, liegt daran, dass in einem Schwerefeld die Zeit ja langsamer vergeht. Da wir die Zeitkomponente bei der Berechnung der Raumzeit-Strecke ja abziehen, ist es günstiger, das Licht auf einer Bahn zu bewegen, die etwas weiter außen liegt. (Eine schöne und einigermaßen nachvollziehbare Berechnung der Lichtablenkung findet ihr in diesem paper von Lerner. (Cool, habe gerade das google-Link-fix addon entdeckt, damit man beim Link-Kopieren nicht immer den google-Quark bekommt.))
Und das ist genau die Komplikation, die ich oben erwähnt habe: Ja, im Heiße-Platte-Modell kann man sich anschaulich machen, wie ein Raum gekrümmt sein kann, aber die Raumkrümmung dort entspricht nicht ganz der Lichtablenkung in Schwerefeld, denn die wird zusätzlich auch von der Veränderung des Zeitablaufs beeinflusst. Denn es ist nicht nur der Raum, der gekrümmt ist, sondern die Raumzeit, weil auch die Zeit durch die Massen beeinflusst wird.








Kommentare (61)