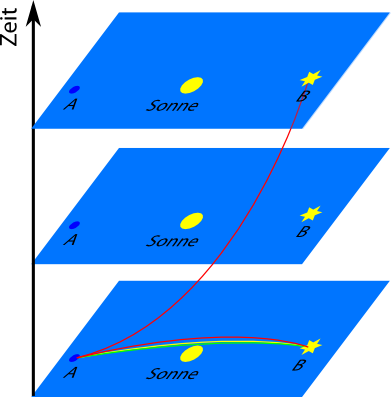
Als letztes können wir zum Beispiel einen Ball werfen. Weil der nicht mit Lichtgeschwindigkeit unterwegs ist, wird er später beim Stern ankommen als das Lichtsignal. Seine Bahn verläuft noch etwas weiter außen:
Wenn man es durchrechnet (ratet mal, wo ich das ausführlich erklärt habe), stellt man fest, dass der kürzeste Weg durch die Raumzeit gerade der ist, den der Ball auf einer Wurfparabel von A nach B nehmen würde. Welche Wurfparabel das ist (man kann den Ball ja flach oder hoch werfen) hängt davon ab, wann der Ball ankommen soll – man darf hier nie vergessen, dass A und B Ereignisse sind, also Punkte in Raum und in der Zeit. Je schneller der Ball unterwegs ist, desto “flacher” verläuft die Parabel.
Für einen fliegenden Ball ist der Raumzeitabstand ds – so wie ich ihn hier definiert habe – negativ. Er hat auch eine direkte physikalische Bedeutung: bis auf das Minuszeichen (hier macht die Wurzel wieder ein wenig Ärger, aber das lässt sich mathematisch schnell in den Griff bekommen, wer’s genauer wissen will, kann bei Wikipedia nachschauen) gibt der Raumzeitabstand ds genau die Zeit an, die auf einer Uhr vergehen würde, die sich mit dem Ball mitbewegt. (Da wir die Strecke minimieren, vergeht für einen Ball also die maximale Zeit.) Für das Lichtsignal ist diese “Eigenzeit” gerade Null. (Wenn man will, kann man das so interpretieren, dass für ein Lichtsignal keine Zeit vergeht – aber Vorsicht: Das ist nur eine anschauliche Interpretation, da sollte man nicht zu viel hineindeuten… Spätestens, wenn man sich überlegt, was dann beim raumartigen Abstand passiert (die Eigenzeit wird negativ?), wird die Sache haarig. (Naja, man könnte jetzt an rückwärts in der Zeit laufende Tachyonen oder so etwas denken…))
Insgesamt sehen wir also: Die kürzeste Verbindung zwischen zwei Punkten (Ereignissen) hängt von der Lage der Punkt im Raum und in der Zeit ab. Licht oder andere Signale laufen nicht einfach auf dem kürzestem Weg im Raum, sondern auf dem kürzesten Weg in der Raumzeit (dem mit der maximalen Eigenzeit).
Die Analogie mit der Platte ist zunächst mal einfach eine andere Art, die Raumkrümmung zu veranschaulichen als die üblichen Bilder von gespannten Gummitüchern und ähnlichem. Sie hat aber gleich zwei Vorteile: Zum einen sieht man unmittelbar, dass man keinen “Hyperraum” oder so etwas braucht, um die Raumkrümmung zu bekommen – die Platte selbst ist und bleibt ja vollkommen flach, es sind die verzerrten Maßstäbe, die für die (scheinbare?) Krümmung sorgen. Und das bringt mich zum zweiten entscheidenen Vorteil: Man kann die Effekte der Raumkrümmung dadurch beschreiben, dass man nicht den Raum beeinflusst, sondern die Materie. Denn in unserem Platten-Modell waren es ja die Maßstäbe, die sich verändern, nicht der Raum. Diese beiden Standpunkte sind nicht unterscheidbar. Und so ist es auch in der ART – man muss sie nicht über die Raumzeitkrümmung verstehen, sondern kann auch mit Teilchen und Kräften arbeiten.
Das funktioniert allerdings nur dann, wenn alle Maßstäbe sich genau gleich verändern. Wenn die Krabbelkäfer auf der heißen Platte Materialien mit unterschiedlichen thermischen Ausdehnungen hätten, dann könnten sie ja direkt die Temperaturänderung bemerken; sie würden dann nicht von gekrümmten Wegen reden, denn die Krümmung würde dann davon abhängen, woraus sie ihre Maßstäbe machen. Wir können die Gravitation also statt über die Raumzeitkrümmung auch durch einen Einfluss auf Materie beschreiben, während die Raumzeit sich ganz normal verhält. Und diese Betrachtungsweise ist insbesondere dann praktisch, wenn man die ART mit der Quantenmechanik unter einen Hut bringen möchte. (Sowohl die Feynman Lectures on Gravitation als auch Steven Weinbergs Buch “Gravitation and Cosmology” verwenden diesen Zugang und führen die geometrische Betrachtungsweise erst später ein.) Dazu schreibe ich aber vermutlich ein andermal etwas…






Kommentare (61)