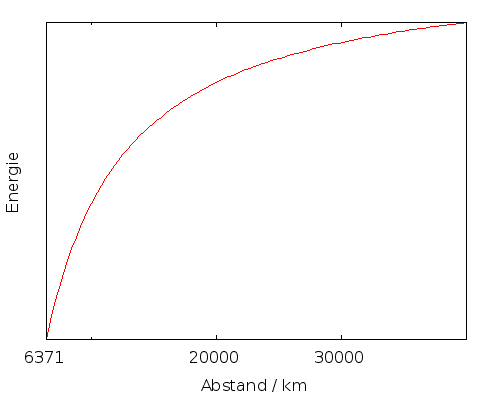
Auf der x-Achse ist dabei der Abstand vom Erdmittelpunkt aufgetragen, und die Kurve fängt bei einem Erdradius an.
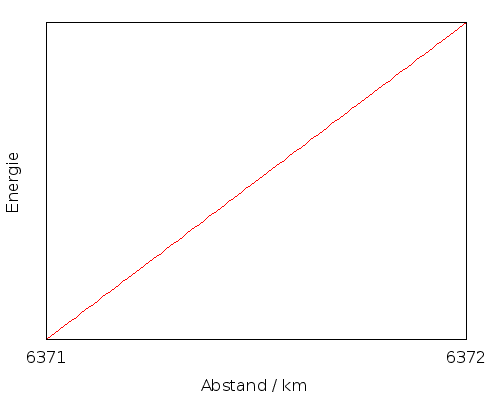
Zoomt man genau bei einem Erdradius in die Kurve hinein, sieht man, dass unsere einfache Formel, bei der die Energie einfach mit der Höhe zunimmt, für kleine Abstände von der Erdoberfläche gut passt – die Kurve ist nahezu perfekt eine Gerade:
Wir können jetzt also die Energie unseres Raumschiffes (zumindest prinzipiell) an Hand dieser Bildchen bestimmen, wenn wir seine Höhe kennen. Das Ganze vereinfacht sich noch etwas, wenn wir zwei Überlegungen anstellen:
1. Wenn wir die Masse des Raumschiffs ändern, dann ändert sich auch die Energie, und zwar genau proportional zur Masse. (Das steckt ja gerade in der Gleichung Kraft gleich Masse mal Beschleunigung: Doppelte Masse gibt doppelte Kraft und damit auch doppelte Energie.) Wir können also eigentlich die Masse des Raumschiffs herausdividieren – dann bekommen wir eine Größe, die das Schwerefeld der Erde selbst charakterisiert, das Potential. Multipliziert man das Potential mit der Masse eines Objekts, erhält man die Energie des Objekts am jeweiligen Ort.
2. Im Moment haben wir den Nullpunkt der Energie (oder des Potentials) genau bei Höhe Null gewählt. Das ist aber eine ziemlich willkürliche Wahl. Wenn wir uns fragen, wie sich die Energie eines Objekts ändert, wenn die Schwerkraft der Erde ins Spiel kommt, dann ist es am einfachsten, den Energienullpunkt so zu wählen, dass das Objekt eine Energie von Null hat, wenn es vom Schwerefeld der Erde nichts merkt. Und das ist dann der Fall, wenn es sehr sehr weit (mathematisch unendlich weit) von der Erde entfernt ist. Nähert sich das Objekt der Erde an, wird seine Energie dann immer kleiner, also negativ. Das klingt vielleicht erst mal seltsam, ist aber sehr praktisch: Nehmt an, ihr lasst das Objekt los und es fällt zur Erde. Dabei wird es natürlich – weil es auf die Erde zufällt – immer schneller und bekommt deshalb Bewegungsenergie. Diese Bewegungsenergie ist natürlich positiv, und sie ist genau gleich der negativen Energie im Schwerefeld, so dass die Summe immer noch Null ergibt.
Also: Wir haben jetzt ein Potential, das ein Maß für die Energie eines Objekts im Schwerefeld ist (wenn wir die Masse des Objekts ranmultiplizieren, bekommen wir die Energie). Das Potential ist gleich Null, wenn wir sehr weit von der Erde (oder was sonst gerade das Schwerefeld erzeugt) entfernt sind. Trägt man das Potential gegen den Abstand auf, dann bekommt man genau dieselbe Kurve wie oben für die Energie (nur jetzt mit anderen Einheiten, aber da ich die ja eh weggelassen hatte, macht das nichts).
Das Potential hängt dabei nur vom Abstand ab – es ist egal, ob ich über dem Nordpol, über Braunschweig oder über Kapstadt herumschwebe – wenn der Abstand von der Erdoberfläche derselbe ist, ist auch die Energie dieselbe. (Naja, nicht ganz, weil die Erde etwas ungleichmäßig geformt und inhomogen ist, aber das sind so Effekte, die ich als theoretischer Physiker locker unter den Teppich kehre.) Wir können also jedem Punkt im Raum einen Wert des Potentials zuordnen – aber das lässt sich schlecht grafisch darstellen. Deswegen lässt man meist eine Dimension beim Zeichnen weg und zeichnet einen zweidimensionalen Schnitt des Potentials. So sieht er aus (dabei ist angenommen, dass die Erde im inneren vollkommen homogen ist, aber das Potential im Erdinnern ist für uns erst mal egal):

(Bild von AllenMcC, Wikimedia, CC 3.0 License)
Im Englischen nennt man so etwas auch “gravity well” – im Deutschen spricht man manchmal vom “Potentialtopf”, auch wenn der hier nicht sehr topfförmig ist.
Wenn sich ein Objekt in einem solchen Potential bewegt, dann gewinnt es – wie ja eben schon erklärt – an kinetischer Energie, je tiefer es in den Topf hineinrutscht. Die Höhe des Objekts gibt direkt seine Energie an- je tiefer es ist, desto geringer ist seine Energie. (Bindungsenergien werden in der Physik generell negativ gerechnet, warum das sinnvoll ist, habe ich hier erklärt.)






Kommentare (84)