Das Modell des Gummituchs, das sich durchbiegt, wenn man Massen drauflegt, ist ein brauchbares Modell für das Potential des Schwerefelds – allerdings in der klassischen Physik nach Newton. Das habe ich im ersten Teil dieses Textes erklärt. Wie kommt es aber, dass man das Modell so oft im Zusammenhang mit der Allgemeinen Relativitätstheorie (kurz ART) sieht? Passt es da vielleicht auch hin und veranschaulicht die Krümmung des Raumes?
Die Raumkrümmung (eigentlich ist es eine Raum-Zeit-Krümmung, aber erst einmal konzentrieren wir uns auf den Raum) habe ich ja neulich schon etwas ausführlicher erklärt. Kurz gesagt sorgt sie dafür, dass sich Abstände (zum Beispiel die Länge von Maßstäben) von Ort zu Ort ändern können. Mein Lieblingsbeispiel ist die Raumkrümmung um eine massive Kugel herum: Wenn ihr einen Kreis um die Kugel malt und dessen Umfang messt, dann sollte der ach der Gleichung U=2πr mit dem Radius zusammenhängen. Wenn ihr aber tatsächlich ins Innere der Kugel eindringt und den Weg messt, dann stellt ihr fest, dass dieser Weg länger ist, als ihr nach dieser Formel erwarten würdet. Es ist sozusagen nach Innen hin “mehr Raum” da, als man eigentlich erwarten würde (das ist eine etwas ungenaue Beschreibung, aber als Veranschaulichung finde ich sie ganz gut). Andersherum kann man auch sagen: Für eine bestimmte Entfernung in Richtung auf den Mittelpunkt zu ist nicht genug Umfang vorhanden.
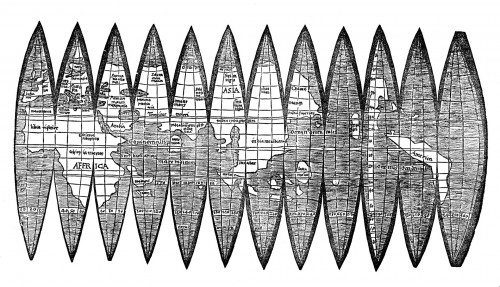
Man kann sich das ganz gut mit einer zweidimensionalen gekrümmten Fläche vorstellen. Wen ihr zum Beispiel eine Mandarine oder Orange schält, und zwar so, dass ihr die Schale möglichst in einem Stück abbekommt, dann könnt ihr die Schale nicht flach auf einem Tisch ausbreiten – wenn ihr das tut, reißt sie ein. Man sieht das auch sehr schön an dieser (sehr alten) Karte, die zur Herstellung von Globen (Globussen, Globunten, Globuli – ach ne, das ist was anderes…) diente:
(Bild von Wikimedia, Public domain)
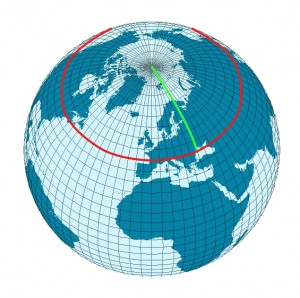
Ihr könnt euch das direkt mit Hilfe von Längen- und Breitengraden veranschaulichen: Je weiter ihr nach Norden geht, um so kürzer wird der Abstand zwischen zwei Längengraden, bis sie dann schließlich am Nordpol alle zusammenlaufen. Das entsprechende Bild von Kreisumfang und -radius habe ich ja schon des öfteren gezeigt:
(Achtung: Bei solchen Analogien läuft man immer Gefahr, durcheinanderzukommen: Es ist die Oberfläche der Erde, um die es jetzt geht, nicht die Erde als Ganzes. Das Innere der Erde ist für die Krümmung irrelevant, und der Mittelpunkt der Erde hier hat nichts mit dem Mittelpunkt zu tun, um den es im vorigen Absatz ging und von dem aus wir den Radius gemessen haben.)
Wen ihr also die Krümmung einer zweidimensionalen Fläche veranschaulichen wollt, dann könnt ihr sie dazu in drei Dimensionen zeichnen, so wie den Globus. (Na klar, der Globus ist tatsächlich ein Objekt in drei Dimensionen – aber das muss für eine gekrümmte Fläche nicht unbedingt gelten; ihr könnt sie auch komplett mit Hilfe von flachen Landkarten beschreiben.) Eine solche Darstellung nennt man auch eine “Einbettung” – die gekrümmte Fläche wird in eine höhere Dimension gepackt oder eben eingebettet.
Um den gekrümmten dreidimensionalen Raum in der ART darzustellen, könnten wir jetzt genauso versuchen, ihn in einem höherdimensionalen Raum darzustellen. (Für den allgemeinen Fall braucht man dazu in der ART aber nicht nur vier, sondern sogar fünf Dimensionen, plus eine Zeitdimension.) Ein Objekt in 4 oder mehr Dimensionen können wir uns aber nicht so leicht vorstellen. Entsprechend begnügt man sich damit, nur einen zweidimensionalen Ausschnitt einzubetten. Damit es nicht zu übermäßiger Verwirrung mit den Globus-Bildern oben kommt, nehme ich jetzt als massives Objekt nicht die Erde, sondern die Sonne:
(Bild mit gimp erzeugt, die Oberfläche der Sonne von Wikimedia, Public domain)







Kommentare (67)