Wir betrachten jetzt eine Schnittebene durch die Sonne (genau durch ihren Mittelpunkt, naja, hab ich nicht ganz perfekt gezeichnet), etwa so:
Jetzt haben wir eine zweidimensionale Ebene im Raum. Diese Ebene ist aber – wegen der Raumkrümmung – eben gekrümmt. Wenn wir also den Umfang des roten Kreises messen und daraus den Sonnenradius berechnen, kommen wir auf einen anderen Wert, als wenn wir tatsächlich die Strecke bis zur Mitte der Sonne ausmessen (der Unterschied beträgt etwa 500 Meter, das ist bei einem Sonnenradius von etwa 700000 Kilometern nicht schrecklich viel, aber immerhin).
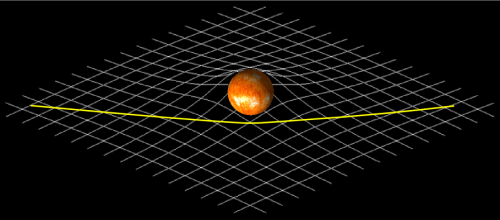
Genau wie bei der Orange von vorhin oder bei dem Schnittmuster für den Globus “fehlt” uns also etwas Raum, wenn wir versuchen würden, den Raum tatsächlich “flach” zu drücken. Wir können, um das zu veranschaulichen, den Raum um die Sonne herum (aber nur unseren Schnitt entlang der Ebene) in den dreidimensionalen Raum einbetten und sehen, was passiert. Das Ergebnis sieht so aus:
In der Mitte sitzt hier die Sonne (da wo die Fläche eher wie eine Kugel gekrümmt ist). Ihr seht auch in diesem Diagramm, dass ihr eine größere Strecke bis zum Mittelpunkt der Sonne zurücklegen müsst, als ihr eigentlich erwarten würdet, wenn ihr nur den Umfang eines Kreises betrachtet:
Ein solches Bild bezeichnet man auch als Einbettungsdiagramm. Man kann es auch direkt in ein dreidimensionales Bild hineinzeichnen, obwohl das ein bisschen verwirrend ist – zur Veranschulichung wird das aber gern gemacht, etwa so:
(Bild von Wikimedia, Public domain)
Ein solches Bild ist ein bisschen irreführend, weil die dritte Dimension hier gleich eine Doppelrolle spielt – zum einen wird sie verwendet, um zu zeigen, wie sich Strecken ändern, wenn man dichter an die Sonne herangeht, zum anderen braucht man sie aber auch für die 3D-Darstellung der Sonne und des ganzen anderen Krams im Bild. (Die dargestellte Raumkrümmung entspricht auch eher der Form eines Newton-Gravitationspotentials, aber das ist bei solchen Darstellungen auch oft so – auch bei dem Bild, das ich gleich zeige.)
Wichtig an den Einbettungsdiagrammen ist, dass man sie – wie wir eben am Bild mit dem Kreis gesehen haben – verwenden kann, um zu sehen, wie sich Strecken ändern, wenn man einen gekrümmten Raum durchquert. Die Diagramme werden aber auch gern verwendet, um zu zeigen, wie sich Objekte in der Raumzeit bewegen. Beispielsweise wird die Lichtablenkung gern mit solchen Bildern dargestellt (siehe auch das Bild eben, wo ja auch ein Signal abgelenkt wird)):
(Bild der Raumkrümmung von Wikimedia, CC License 3.0; mit Inkscape und gimp modifiziert. Auch hier ist die Raumkrümmung quantitativ falsch.)
Solche Bilder sind allerdings problematisch. Die Bewegung von Licht oder von Teilchen wird nämlich nicht nur durch den gekrümmten Raum beeinflusst, sondern durch die Krümmung der Raumzeit – dass die Zeit in der Nähe eines Schwerefelds anders verläuft, spielt eine wichtige Rolle, wie ich neulich ja schon erklärt habe.
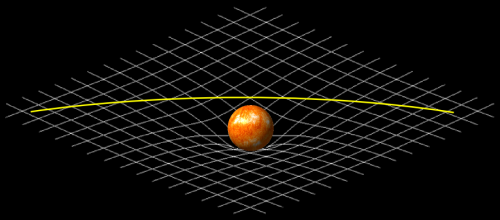
Wenn wir aber einmal den Aspekt der veränderten Zeit ignorieren, dann sehen wir bei Bildern dieser Art immer noch folgendes: Der Lichtstrahl nimmt hier den kürzesten Weg (wie gesagt, das stimmt nicht ganz wegen der Zeitkomponente) – die Raumkrümmung wirkt eben dadurch, dass in der Nähe der Masse Strecken verändert sind. Es spielt deshalb überhaupt keine Rolle, wie wir unser Bild zeichnen. Wir könnten es beispielsweise genausogut herumdrehen (ich hätte eigentlich die Sonne jetzt unter die gekrümmte Fläche malen sollen, aber das war mir zu viel Arbeit…):
Entscheidend ist einzig und allein, dass sich Längen verändern – ob die Krümmung nach oben oder unten läuft, spielt überhaupt keine Rolle.
So, und jetzt kommen wir zurück zum Gummituch. Hier noch einmal das Bild des Gravitationspotentials vom letzten Mal

(Bild von AllenMcC, Wikimedia, CC 3.0 License)










Kommentare (67)