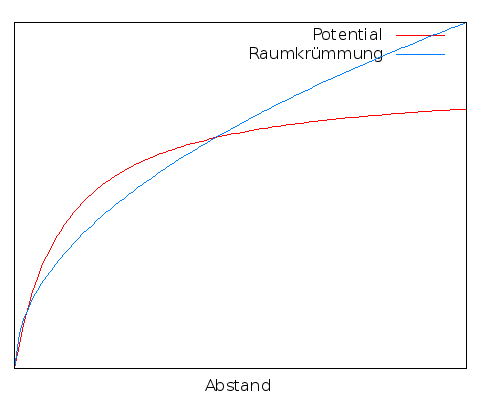
Dieses Bild zeigte die Energie (oder das Potential) eines Teilchens im Schwerefeld an. Zunächst einmal sieht man, wenn man es mit dem Bild des gekrümmten Raums oben vergleicht, dass die Form eine andere ist – auch mathematisch passen die beiden Bilder nicht zusammen.Hier ein direkter Vergleich der Form als Funktion des Abstands – einmal für das Potential (oder eben die Form des Gummituchs, in rot), einmal für die Form des Modells des gekrümmten Raums (blau):
Das allein ist schon ein gutes Argument dafür, dass das Bild des Gummituchs (das ja auf diesem Potential beruhte) nicht viel mit der Raumkrümmung zu tun hat.
Aber gut – auch wen es mathematisch nicht so gut passt, ist es vielleicht doch eine gute Veranschaulichung, oder? Nein, leider nicht. Dazu muss man sich nur überlegen, was passiert, wenn man das Gummituch beispielsweise einfrieren und dann umdrehen würde. Im Bild des gekrümmten Raumes ist das vollkommen egal, wie wir gerade gesehen haben. Eine Kugel, die über unser umgedrehtes Gummituch rollt, benimmt sich aber ganz anders als eine, die auf dem normalen Gummituch herumkullert – auf dem umgedrehten Tuch wird die Kugel ja von den Beulen im Tuch abgestoßen und nicht angezogen. Die Bewegung der Kugeln auf dem Gummituch wurde ja durch die Schwerkraft (die hier konstant war und dafür sorgte, dass sich die Energie der Kugel proportional zur Höhe des Tuchs ändert) bestimmt – im Bild der Raumkrümmung aber spielt das gar keine Rolle, denn da geht es nur darum, welche Wege die kürzesten sind. (Das passt auch zu der Aussage, dass es in der ART gar keine Schwerkraft gibt – entsprechend ergibt es auch wenig Sinn, von potentieller Energie zu reden.)
Hmm – aber wie funktioniert eigentlich die Anziehung in unserem Raumkrümmungsmodell?
Erst einmal gar nicht. Wenn ihr eine Kugel irgendwo platziert, ohne dass sie sich bewegt, und es keine Anziehung oder so etwas gibt, dann würde die Kugel einfach am Ort verharren. Dass reale Kugeln sich bewegen, liegt an der Krümmung der Raumzeit. Die sorgt dafür, dass eine ruhende Kugel, die sich in der Nähe einer Masse befindet und bei der deshalb die Raumzeit gekrümmt ist, bewegt. Wie das? Ausführlich habe ich das auch hier erklärt – kurz gesagt liegt es daran, dass eine Bewegung im freien Fall in der gekrümmten Raumzeit dem entspricht, was eine Bewegung mit konstanter Geschwindigkeit in einer ungekrümmten Raumzeit ist. Ein Objekt im freien Fall folgt sozusagen der natürlichen Bahn in der Raumzeit (so wie in der klassischen Physik nach Newton ein kräftefreies Objekt mit konstanter Geschwindigkeit weiterfliegt, das ist das berühmte erste Newtonsche Axiom).
Das ist übrigens noch ein weiteres Argument gegen das Gummituchmodell: Die Krümmung des Raums allein reicht nicht aus, um die Bewegung von Teilchen zu erklären – und tatsächlich wird sich kein Teilchen (und auch kein Lichtstrahl) auf der Bahn bewegen, die im gekrümmten Raum der kürzesten Strecke entspricht, weil die Zeitkomponente der Raumzeit dies verhindert. (Das habe ich ja neulich ganz ausführlich auseinandergedröselt.) Sonst wäre es auch nicht zu erklären, dass die ART und das Newtonsche Modell in den meisten Fällen sehr ähnliche Vorhersagen machen – die Bahnen der Planeten werden ja, abgesehen von dem sehr winzigen Effekt der Periheldrehung, von beiden Theorien gleich gut vorhergesagt.
Das Gummituch-Modell illustriert eigentlich nur eins: Dass Massen den Raum irgendwie krümmen.Die Krümmung im Gummituch-Modell sorgt aber nicht dafür, dass Kugeln in diesem Modell auf kürzesten Verbindungen zwischen zwei Raumzeitpunkten laufen (so wie sie es in der ART tun), sondern dafür, dass sich die Energie von Ort zu Ort so ändert, wie sie es in der klassischen Physik tut. Die Bewegung von Teilchen in diesem Modell stimmt zwar mit der Bewegung von Teilchen in der ART näherungsweise überein, aber eben nicht, weil das Modell ein gutes Modell der Raumkrümmung ist, sondern weil die Energielandschaft der klassischen Physik für nahezu die selben Bewegungen sorgt wie die gekrümmte Raumzeit der ART.






Kommentare (67)