Horizontal ist hier die Festigkeit des Bodens aufgetragen, auf der senkrechten Achse der Druck. Nur bei genau passenden Werten landet man in der goldenen Goldilocks-Zone, sonst ist der Boden entweder zu weich oder zu hart.
Als ich das paper – mehr oder weniger per Zufall – las, dachte ich “Kann nicht sein.” Zum einen, weil ich aus der Alltagserfahrung wusste, dass z.B. an einem Strand sowohl ich als auch ein Kind gleichzeitig sichtbare Spuren hinterlassen können. Zum anderen, weil es in der Materialwissenschaft ein Standardverfahren ist, Eindrücke in Werkstoffe zu machen, um deren Festigkeit zu testen, und dort muss man nicht den Druck, mit dem man arbeitet, ganz genau einstellen, damit der Indenter nicht metertiefe Krater macht. Ich war also skeptisch.
Mehr oder weniger durch einen weiteren Zufall (über einen gemeinsamen Bekannten) bekam ich dann Kontakt zu Peter und wir trafen uns in Obernkirchen bei der großartigen Dino-Fußspur-Konferenz. Peter machte mir erst einmal klar, dass meine Vorstellung von Fußabdrücken eventuell etwas zu simpel ist – beim Menschen ist es wegen der gewölbten Fußfläche so, dass bei tieferen Eindrücken immer mehr Fußfläche mit dem Boden in Berührung kommt. Bei unseren Eindrücken zur Materialprüfung ist das ganz ähnlich – dort verwenden wir Kugeln oder diamantförmige Indenter – je größer die Kraft wird, desto größer ist die Fläche, die in Berührung kommt, so dass sich die Kraft auch weiter verteilt. Die meisten Vögel (und vermutlich auch Dinos) hatten aber eher flache Füße, so dass der Effekt dort kleiner sein sollte. Trotzdem war ich nicht überzeugt – bei einer genaueren Simulation, bei der Material verdrängt werden und sich aufstauen kann würde der Effekt größtenteils verschwinden, so meine Annahme.
Und wenn man sich in der Wissenschaft uneinig ist, so wie wir hier, dann ist der beste Weg, einfach zusammenzuarbeiten und zu sehen, was man herausbekommt. Und das taten wir dann auch. Ich bastelte also ein Fußspurenmodell, bei dem der Fuß auch tatsächlich tiefer in das Substrat eindringen kann und bei dem die Verdrängung von Material und die Reibung zwischen Fuß und Boden korrekt berücksichtigt werden sollten. Das erwies sich als etwas trickreicher als ursprünglich angenommen, aber schließlich klappte es.
(Wenn ihr es genau wissen wollt: Das Problem sind die sehr großen Deformationen im Boden, die durch die Verdrängung entstehen. Die führen zu einer starken Verzerrung des ursprünglichen Rechengitters, weil man bei der FE-Methode das Gitter an das Material anheftet. Zum Glück erlaubte die damals neuste Version meines FE-Programms schließlich, ein Gitter zu verwenden, das im Raum feststeht und durch das das Material durchfließt – damit ging es dann. Allerdings war ein bisschen Trickserei nötig, bis alles vernünftig herauskam – zum Glück fand ich einen Studi, der sich für’s Thema begeistern konnte, denn das Simulieren von Fußspuren ist ja nicht meine Hauptaufgabe…)
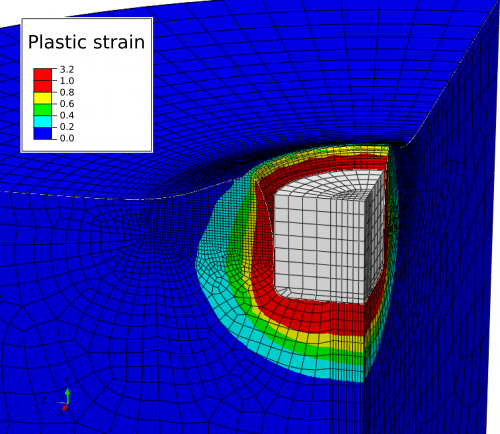
Da ich ja theoretischer Physiker bin, habe ich es mir dabei mit dem Fuß recht einfach gemacht und angenommen, dass der Fuß ein Zylinder (mit leicht abgerundeten Kanten) ist – das ist als sehr grobe Näherung an einen Sauropodenfuß vielleicht gar nicht so schlecht, und es ging ja auch und vor allem ums Prinzip. Wegen der Symmetrie habe ich nur ein viertel des Zylinders modelliert und den dann (wie gesagt, mit fleißiger Unterstützung eines Studis) in den Boden eindringen lassen, was etwa so aussah (die Farbe kennzeichnet, wie stark der Boden verformt wurde):
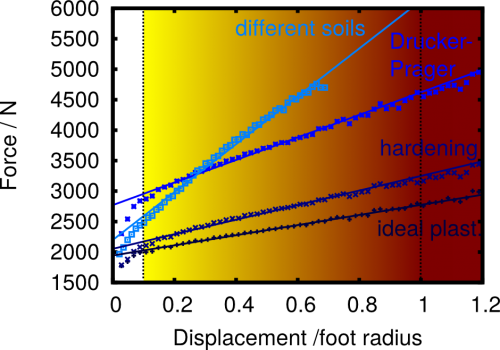
Und dann haben wir – für verschieden komplexe Bodenmodelle, auf die Details gehe ich aber nicht ein, wer die wissen will, kann ja ins paper schauen – die Kraft als Funktion der Eindringtiefe berechnet. So sah das Ergebnis aus:
Ihr seht, dass mit zunehmender Eindringtiefe (auf der horizontalen Achse) die Kraft ungefähr linear zunimmt. Es gibt also einen ganzen Bereich von Kräften, mit denen man Fußspuren erzeugen kann. Wir haben angenommen, dass der flachste Abdruck, den man noch erkennen kann, ein Zehntel des Fußradius groß ist, der tiefste Abdruck gleich dem Fußradius (noch tiefer einzusinken ist sicher unangenehm). Abhängig von den Annahmen, die man über den Boden macht, ergibt sich dabei ein mehr oder weniger großer Bereich von Kräften, mit denen man hier Abdrücke erzeugen kann. Der Goldilocks-Effekt ist also nicht so stark, wie ursprünglich angenommen, insbesondere dann nicht, wenn man komplexere Bodenmodelle annimmt, bei denen der Boden unter dem anliegenden Druck verfestigt oder bei dem unterschiedlich feste Bodenschichten übereinander liegen (“different soils” im Bild).







Kommentare (28)