Wenn man versucht, sich Schwarze Löcher vorzustellen, dann ist man leider leicht verwirrt. Das liegt nicht nur daran, dass Schwarze Löcher nun mal ziemlich komplizierte Gebilde sind, sondern zumindest teilweise auch daran, dass man das, was in der Nähe eines Schwarzen Lochs passiert, aus großer Entfernung nur schlecht beschreiben kann. Heute versuche ich es mit einem Trick – dazu fülle ich das ganze Universum mit Staub und gucke, was passiert. Am Ende werden wir bei einer netten Veranschaulichung des Schwarzen Lochs landen, die vielleicht ein bisschen weiterhilft, das ganze zu durchschauen.
Dieser Text ist übrigens mal wieder ein kleiner Baustein in meinem Versuch, die Allgemeine Relativitätstheorie (ART) selbst halbwegs anschaulich zu verstehen – ein echter ART-Experte bin ich nicht und ich übernehme wie üblich keine Garantie, dass ich nicht irgendwo etwas durcheinandergebracht habe. Was ich mit “anschaulich” meine, habe ich übrigens vor langer Zeit in diesem Artikel mal erklärt.
Wir fangen ganz simpel an – mit dem Universum nach Newton. (Naja, eigentlich hat Newton selbst sein eigenes Universum nicht zu 100% richtig verstanden, aber das werden wir gleich noch sehen.) Betrachten wir zunächst ein völlig leeres Universum. O.k., das ist unendlich langweilig. Wir sollten zumindest irgendwas in unserem Universum drin haben – stecken wir einfach eine Beobachterin hinein. (Traditionell heißt die wie in der Kryptographie Alice.) Wenn Alice mutterseelenallein im Universum ist, ist es für sie immer noch beliebig langweilig – sie kann nicht einmal feststellen, ob sie sich bewegt oder still steht, weil es nichts gibt, relativ zu dem sie sich bewegen könnte. (Ob Alice in einem vollkommen leeren Universum feststellen könnte, ob sie sich dreht, ist eine andere Frage – das Problem wird hier bei Wikipedia erklärt, aber ich ignoriere das erst mal.)
Aber vielleicht hat Alice ja irgendetwas dabei – einen Ball beispielsweise. Den könnte sie dann werfen und seine Bahn verfolgen. Um sich das etwas einfacher zu machen, kann Alice das ganze Universum mit magischem Staub anfüllen (hey, das hier ist ein Gedankenexperiment, wir haben gerade ein Universum geschaffen und jemanden reingesetzt, da sprengt ein bisschen Staub die Vorstellungskraft auch nicht mehr, oder?). Dieser magische Staub hat die Eigenschaft, dass auf ihn keine Kräfte wirken – außer der Gravitation, die wir später einführen werden. Magisch ist er, weil ich annehme, dass wir ihn trotzdem irgendwie “sehen” können, ohne dass ich mir Gedanken darüber mache, dass er dann ja möglicherweise auch von elektrischen Feldern beeinflusst werden könnte. Und magisch ist er auch insofern, als ich annehme, dass ich das ganze Universum damit anfüllen kann, so dass die Staubkörner schön regelmäßig verteilt sind (vielleicht alle im Abstand von einem Zentimeter), ohne dass die Masse der Staubkörner selbst irgendeinen Einfluss aufs Universum hat. (Wir werden nachher sehen, dass man so einen Staub in der Kosmologie auch gern verwendet…)
Wenn Alice einen Ball wirft (ich nehme mal an, der ist so leicht, dass sie selbst dabei nicht beschleunigt wird), dann kann sie sehen, wie er sich relativ zum Staub bewegt und so seine Bewegung messen. Das gleiche kann sie auch tun, wenn sie in ihrem Universum Gesellschaft bekommt – schicken wir am besten Bob in Alice’s Universum, dann wird es dort interessanter (nein, nicht was ihr wieder denkt…). Bob kann sich relativ zu Alice mit konstanter Geschwindigkeit bewegen – und Bob kann auch seinen eigenen Staub haben, der relativ zu ihm ruht. Von Alice aus gesehen, bewegt sich Bob (was sie daran sehen kann, dass er zu unterschiedlichen Zeiten an unterschiedlichen Staubkörnern ist) – von Bob aus gesehen ist es umgekehrt.
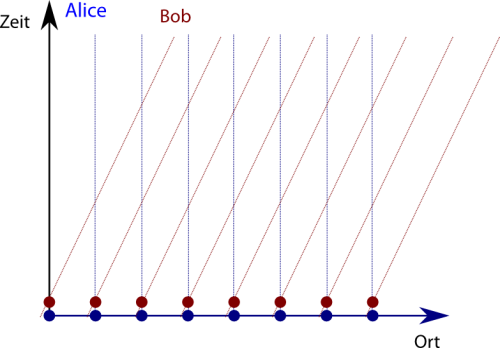
So sieht die Situation von Alice aus betrachtet aus: (Die Zeitachse ist dabei schwarz, weil sie für beide dieselbe ist), die Kreise sollen die Staubkörner symbolisieren:
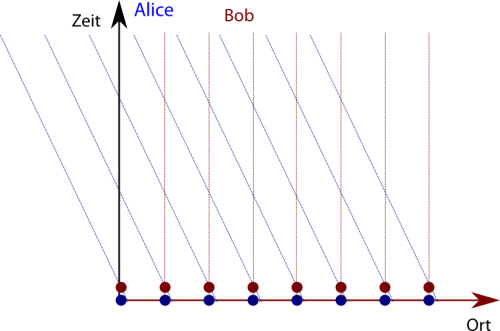
Und so sieht es für Bob aus (für den es Alice ist, die sich bewegt, und zwar in die andere Richtung):
Es gibt keine Möglichkeit, zu sagen, wer von beiden Recht hat – und das ist der kleine Fehler, den der gute Newton mit seiner Annahme vom absoluten Raum gemacht hat. Es ist unmöglich, festzustellen, ob ich mich relativ zum “absoluten Raum” mit gleichförmiger Geschwindigkeit bewege oder nicht. Man kann das auch anders ausdrücken: Es ist nicht möglich, zwei Raumpunkte zu unterschiedlichen Zeiten eindeutig in Beziehung zu setzen und zu sagen, ob es sich um denselben Raumpunkt handelt oder nicht – für Alice sieht die Sache anders aus als für Bob. Worüber sich aber beide einig sind, ist der Verlauf der Zeit – wenn für Alice eine Sekunde vergeht, tut sie das auch für Bob. (Newton hatte einen plausiblen Grund, anzunehmen, dass es einen absoluten Raum gibt, weil er wusste, dass man Drehungen im Universum eindeutig feststellen kann (siehe auch oben). Daraus hat er – fäschlicherweise – auf den absoluten Raum zurückgeschlossen.)
Innerhalb der Newtonschen Welt gibt es nicht mehr viel weiteres zu sagen. (Und das, was ich gerade hier erzählte, habe ich schon vor ziemlich genau einem Jahr in anderem Zusammenhang erklärt.)
Falls ihr euch die ganze Zeit fragt, warum ich nicht einfach ein Koordinatensystem einführe, sondern ständig von Staub rede – der Staub hat den Vorteil, dass es sich um echte physikalische Teilchen handelt – Koordinaten kann man so absurd definieren, wie man will (ein Beispiel dafür sehen wir noch), aber echte physikalische Teilchen können auch nur Dinge tun, die physikalisch möglich sind.
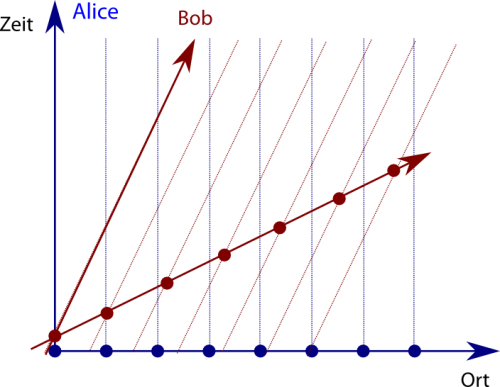
Betrachten wir als nächstes die spezielle Relativitätstheorie (SRT). Eine zentrale Aussage der Theorie ist ja, dass sich Objekte relativ zueinander nicht mit Überlichtgeschwindigkeit bewegen können. Wenn wir also die Staubteilchen betrachten, dann ist klar, dass wir uns relativ zu Alices Staub nicht überlichtschnell bewegen können – relativ zu Bobs Staub übrigens auch nicht. (Die berühmten Additionsregeln für Geschwindigkeiten in der SRT sorgen dafür, dass es keine Probleme gibt, wenn sich Bob mit nahezu Lichtgeschwindigkeit von Alice entfernt und Claudia mit nahezu Lichtgeschwindigkeit von Bob – von Alice aus gesehen ist Claudia trotzdem nicht überlichtschnell.) Das Diagramm für Alice sieht jetzt so aus:
Dabei sind jetzt die Orts- und Zeitachsen gegeneinander verkippt, weil in der SRT Raum und Zeit ja zusammen die Raumzeit bilden. (Achtung, das Diagramm ist nicht gerechnet, sondern nur qualitativ korrekt.) Da wir die Umrechnung zwischen unterschiedlichen Beobachtern nicht wirklich detailliert brauchen, spare ich mir die detailliertere Erklärung, ein bisschen was zu diesen Diagrammen haben ich hier und hier geschrieben. Wenn ihr mit solchen Diagrammen herumspielen wollt, gibt es dafür sogar eine interaktive Grafik.
Machen wir jetzt den Sprung zur Allgemeinen Relativitätstheorie. Hier wird das Staub-Bild tatsächlich gern verwendet, jedenfalls in der Kosmologie. Um sich die Ausdehnung des Universums zu veranschaulichen, kann man sich Staub vorstellen, der kurz nach dem Urknall gleichmäßig verteilt das Universum erfüllt. Dehnt sich das Universum aus, dann entfernen sich die Staubteilchen voneinander – wie genau sie das tun, kann man dann anschauen, um die Details der Expansion des Universums zu verstehen. Hier sieht man jetzt den Vorteil des Staub-Bildes: Der Staub veranschaulicht direkt die Ausdehnung des Raums. Man kann so tun, als würde jedes Staubkorn einen Raumpunkt kennzeichnen und kann dann direkt sehen, wie sich die Raumpunkte zueinander verhalten – die sich entfernende Staubteilchen folgen dem sich ausdehnenden Raum, und man kann so tun als würde man direkt sehen, wie sich der Raum dehnt, wenn man die Staubteilchen betrachtet.
Aber auch dabei darf man nicht vergessen, dass es nicht nur eine Möglichkeit gibt, den Staub anzuordnen. Typischerweise betrachtet man Staub, der relativ zur sonstigen Materie (und auch relativ zur kosmischen Hintergrundstrahlung) im Universum ruht (oder man nimmt den Staub gleich als Modell für die Materie im Universum) – aber auch hier ist es egal, wenn sich Bob relativ zu Alice mit gleichförmiger Geschwindigkeit bewegt, auch er beobachtet die Expansion des Universums in seinem Bezugssystem. Da ich die Expansion des Universums vor einiger Zeit ausführlicher diskutiert habe, brauche ich hier auf die Details nicht einzugehen. (In den Kommentaren gibt es eine lange Diskussion zur Frage des Vergleichs zwischen Alice und Bob, ich bin aber immer noch der Ansicht, dass beide Standpunkte gleichberechtigt sind; wir können das aber gern noch mal in den Kommentaren diskutieren.)
Das Staub-Bild wird typischerweise nicht verwendet, wenn man es mit der Gravitation von Massen zu tun hat, beispielsweise mit Sternen oder gar Schwarzen Löchern. Dort ist es aber eigentlich besonders nützlich, wie wir gleich sehen werden.
Am Anfang stellt sich aber erst einmal ein Problem: Stellt euch Alices Universum vor, angefüllt mit Staub, der relativ zu Alice ruht. Jetzt bringen wir (wie auch immer wir das tun) eine Masse in dieses Universum, der Einfachheit halber so, dass die Masse auch relativ zu Alices Staub in Ruhe ist. Diese Masse zieht unseren Staub jetzt an, so dass er auf die Masse zuzustürzen beginnt. Verfolgen wir den Staub über eine Weile, so sehen wir, dass die Staubteilchen, die von Außen kommen, immer weiter auf die Masse im Zentrum zustürzen – unser Bild des Staubs ist nicht zeitunabhängig. Das ist unschön, denn das Schwerefeld einer Masse ist ja zeitunabhängig immer gleich – unser Staub verdeckt das und macht die Sache so etwas unanschaulich.
Nebenbemerkung: Was genau am Anfang passiert, wenn wir die Masse ins Universum bringen, hängt ein bisschen davon ab, wie wir das machen. Die Gleichungen der ART erlauben es nicht, eine Masse einfach an einer Stelle aus dem Nichts entstehen zu lassen (in der Elektrodynamik ist das genauso – dort können Ladungen auch nicht einfach an einem Punkt auftauchen). Wir können uns vorstellen, wir würden die Staubteilchen erst einmal festhalten und dann zu irgendeinem Zeitpunkt loslassen, so dass sie ab diesem Moment frei fallen können.
Wir können aber einen Trick verwenden, um doch noch Nutzen aus den Staubkörnern zu ziehen: Wir warten. Und zwar warten wir sehr, sehr lange. Nach sehr langer Zeit sind alle Staubkörner, die dicht an unserer Masse gestartet sind, auf diese Masse draufgestürzt (da die Masse der Staubkörner beliebig klein ist, ändert das nichts am Schwerefeld). Alle Staubkörner, die wir noch sehen, sind dann vor sehr langer Zeit in sehr großer Entfernung gestartet. Im mathematischen Grenzfall unendlich langer Wartezeit sind alle Staubteilchen, die wir beobachten, mit Geschwindigkeit Null in unendlicher Entfernung gestartet. Man kann sich das auch andersherum vorstellen: Wir lassen unsere Masse Staubkörner aussenden, und zwar genau mit der Fluchtgeschwindigkeit, so dass die Körner nach außen fliegen, dabei immer langsamer werden und schließlich nach unendlich langer Zeit gerade Geschwindigkeit Null erreichen.
So sieht der Strom der Staubteilchen schließlich aus: Sie stürzen alle mit zunehmender Geschwindigkeit auf unsere Masse zu:
Bisher haben wir eher eine Newtonsche Sicht der Dinge verwendet – die Masse zieht die Staubkörner an und deswegen stürzen sie auf die Masse zu. Einstein würde die Sache anders betrachten: Nach Einstein gibt es ja keine Schwerkraft, sondern die Effekte der Schwerkraft kommen dadurch zu Stande, dass Teilchen kräftefreie Bahnen in der Raumzeit ziehen. Wenn keine Kräfte wirken, dann fliegen Teilchen einfach mit konstanter Geschwindigkeit (das ist das erste Newtonsche Axiom), die kräftefreien Bahnen (Geodäten genannt) sind also einfach Geraden, auf denen die Teilchen konstante Geschwindigkeiten haben. (Ausführlich habe ich das auch in diesem Text erklärt.) Die Masse krümmt jetzt die Raumzeit und beeinflusst so die Bahnen der Teilchen. Unsere Staubkörner fallen also nicht auf die Masse zu, weil sie von einer Kraft angezogen werden, sondern weil die Masse die Raumzeit so verändert, dass das Fallen zur Masse jetzt die kräftefreie Bewegung ist, sozusagen die geradlinigste Bewegung, die möglich ist.
So ähnlich war es ja eben auch beim expandierenden Universum: Dort veränderte sich die Raumzeit so, dass die Abstände zwischen den Staubteilchen immer weiter zunahmen – jedes Staubteilchen für sich genommen “merkt” nichts von der Ausdehnung des Universums, sondern staubt einfach so vor sich hin (oder was immer Staubteilchen tun). Allerdings war das sich ausdehnende Universum überall gleich. Bei unserer Masse im Universum merkt auch keins der Staubteilchen etwas von irgendeiner Schwerkraft oder Raumzeitkrümmung – es folgt einfach seiner kräftefreien Bahn, nur dass diese Bahn jetzt für unterschiedliche Staubkörner unterschiedlich ist.
Wenn unsere Masse, auf die die Staubteilchen zustürzen, ein Schwarzes Loch (kurz SL) ist, dann fallen die Staubteilchen genau am Rand des Schwarzen Lochs (am Ereignishorizont) mit Lichtgeschwindigkeit relativ zum Ereignishorizont. (Das ist der rote Kreis oben im Bild.) Da sich kein Körper relativ zu einem anderen mehr als lichtschnell bewegen kann (Spekulationen über Tachyonen lasse ich mal außen vor…), kann also kein Körper dem Schwarzen Loch entkommen, wenn er den Bereich erreicht, bei dem der Staub lichtschnell fällt. Umgekehrt sieht man aber auch, dass der fallende Staub selbst am Ereignishorizont keine Besonderheiten sieht (wenn Staub etwas sehen kann) – das einzelne Staubteilchen ist ja im freien Fall, fühlt sich kräftefrei (um etwas von Gezeitenkräften zu merken, die normalerweise jeden, der in ein SL stürzt, spaghettifizieren, ist es zu klein) und merkt nichts davon, dass es – von Außen betrachtet – gerade einen Punkt ohne Wiederkehr überschritten hat.
Bei diesen Überlegungen ist es jetzt etwas haarig mit den Bezugssystemen – kein Teilchen kann relativ zum anderen mit Lichtgeschwindigkeit fliegen – aber der Ereignishorizont ist kein Teilchen, für ein physikalisches Objekt ist es unmöglich, starr am Ereignishorizont zu verharren. (Ein Photon könnte allerdings genau am Ereignishorizont quasi “eingefroren sein und dort “schweben”.) Das ist auch genau der Grund, warum es in der oft verwendeten Schwarzschild-Metrik am Ereignishorizont zu Problemen kommt. (Innerhalb des Ereignishorizonts ist es noch haariger – auf dem Bild fallen die Teilchen dort mit Überlichtgeschwindigkeit – aber das tun sie relativ zu einem Beobachter, der an einer Position innerhalb des Ereignishorizonts stehen bleibt, und so einen Beobachter kann es nicht geben, weil innerhalb des Horizonts alles nach Innen stürzt. Die genaue Interpretation des Bildes erfordert ein bisschen Mathematik.)
Wenn wir – so wie bei der Ausdehnung des Raums – wieder die Staubteilchen als “Marker” für Raumpunkte betrachten (mit allen Vorbehalten, weil es ja unterschiedliche Bezugssysteme gibt, die alle gleich gut sind), dann können wir das Bild auch noch etwas anders interpretieren: Wir können sagen, dass bei einer Masse der Raum selbst auf die Masse zustürzt. Klingt etwas absurd, aber wenn Raum sich ausdehnen kann, dann kann er auch “stürzen”, oder? Das ist das “Wasserfall-” oder “Fluss-“Modell der Schwerkraft, das zum Beispiel hier und hier diskutiert wird. (Diese beiden Links haben mich auch auf dieses Konzept aufmerksam gemacht.) So sieht das Ganze in einer Animation aus (Dank an Andrew Hamilton, der mir erlaubt hat, die hier einzubauen.):
Man kann sich also vorstellen, dass ein Teilchen, das versucht, dem SL zu entkommen, vom in das SL fallenden Raum mitgerissen wird – so wird es auch in den beiden zitierten Seiten beschrieben. Damit ist auch anschaulich klar, warum das Photon am Ereignishorizont verharren kann – es fliegt lichtschnell, aber der Raum stürzt ebenfalls lichtschnell unter ihm ins Schwarze Loch, und so kann es, wie Alice im Wunderland, nur gerade am Ort (dem Ereignishorizont) bleiben, wenn es so schnell läuft, wie es kann.
Der ins SL stürzende Raum ist ein durchaus schönes und anschauliches Bild – es hat allerdings auch einen Haken: Wenn man mit einem Boot in einem Fluss treibt und anfangs eine Geschwindigkeit relativ zum Wasser hat, dann wird die Geschwindigkeitsdifferenz zwischen Boot und Wasser im Laufe der Zeit immer kleiner, weil es ja eine Reibung zwischen den beiden gibt. Nach einer Weile bewegt sich das Boot genau mit der Geschwindigkeit des Wassers und ruht relativ zum Wasser. Das ist beim Raum anders: Stellt euch einen Raum ganz ohne Masse und Schwerkraft zu, in dem der Raumzeitstaub also (beispielsweise in Alices Bezugssystem) ruht. Wenn ihr euch anfangs relativ zu Alices Staub bewegt, dann werdet ihr eben nicht abgebremst (sonst hätten wir Physik nach Aristoteles), sondern behaltet die Geschwindigkeit bei. Beim Sturz auf eine zentrale Masse ist es ähnlich – ein Stein, den ich mit Wucht nach unten schmeiße, stürzt schneller als einer, den ich einfach loslasse. Auch dabei ist allerdings Vorsicht geboten: Vom Standpunkt eines Beobachters, der direkt am Ereignishorizont sitzt, falle beide Teilchen am Ereignishorizont lichtschnell; relativ zueinander sehen die beiden Teilchen das jeweils andere aber nicht still stehen, sondern sich bewegen.
Damit die Analogie mit dem Wasserfall perfekt stimmt, bräuchte man also so etwas wie reibungsfreies Wasser, in dem man aber trotzdem nicht schneller als z.B. mit Schallgeschwindigkeit schwimmen kann. Insofern passt das Bild des Raumzeit-Wasserfalls in meinen Augen nicht zu 100%. Trotzdem ist es eine gute Veranschaulichung. Das Bild lässt sich übrigens auch für rotierende Schwarze Löcher erweitern, folgt den beiden Links oben, wenn ihr dazu mehr wissen wollt.
Falls ihr jetzt die Frage stellt, ob der Raum “wirklich” ins Schwarze Loch stürzt – das ist letztlich eine Frage, die man nicht beantworten kann, weil sie sich um die Interpretation einer physikalischen Theorie dreht. Man kann das SL so beschreiben – genauso wie man das expandierende Universum über den sich ausdehnenden Raum beschreiben kann. Man muss das aber nicht tun – alle bekannten Phänomene der Schwerkraft können auch ohne Raumzeitkrümmung nur über Kräfte und Felder ausgedrückt werden, das ist nur normalerweise nicht der Standpunkt, den man in der ART einnimmt, weil er viele Überlegungen verkompliziert. (ElementarteilchenphysikerInnen dagegen bevorzugen oft diesen Zugang – sowohl Feynman als auch Weinberg führen die Interpretation der ART als Raumzeitkrümmung erst recht spät in ihren ART-Büchern ein.) “Raum” oder “Raumzeit” ist eben nichts, das man direkt messen und anfassen kann – so war es ja schon im Newtonschen Universum ganz am Anfang, in dem es auch nicht möglich war, eindeutig zu sagen, welcher Raumpunkt “jetzt” welchem Raumpunkt “gleich” entspricht. Man kann das Bild des Raumzeit-Wasserfalls also verwenden (und als Hilfe für die Intuition ist es auch praktisch), aber es ist eine Veranschaulichung, und selbst nicht unbedingt Bestandteil der Theorie.
Sehr schön auseinandergdröselt sind die unterschiedlichen Bezugssysteme übrigens in diesem Buchkapitel hier: (link vom physicsforum). Das Buch muss ich mir wohl mal besorgen.








Kommentare (109)