Stellt euch also einen Wassertropfen vor (oder für den Frost auf der Scheibe den in der Luft gelösten Wasserdampf, aber ich bleibe mal beim Tropfen, die Logik ist dieselbe), den ihr abkühlt. Wenn ihr genau Null Grad erreicht, dann sollte der Tropfen eigentlich gefrieren (weil das energetisch günstiger ist (oder noch genauer gesagt – siehe den oben verlinkten Artikel und die zugehörige Serie, die ihr rechts unter Artikelserien findet – weil die Freie Energie des festen Zustandes dann kleiner ist als die des flüssigen Zustands.)) Wenn ihr die Temperatur eine Winzigkeit unter Null Grad absenkt, dann ist aber der Gewinn, den ihr habt, auch nur sehr klein. Mit anderen Worten: Die treibende Kraft für den Prozess (wobei man sich unter Kraft jetzt nicht das vorstellen sollte, was man in der Mechanik mal in der Schule gelernt hat, sondern einfach den Energiegewinn, der den prozess antreibt) ist sehr klein. Das ist auch genau der Grund, warum man in der Theorie unendlich lange warten muss – dann setzt sich auch der unendlich kleine Vorteil schließlich durch.
In einem realen Wassertropfen geht die Umwandlung aber natürlich an irgendeinem Punkt los und breitet sich von dort aus – der ganze Wassertropfen erstarrt nicht schlagartig zu Eis. Und das verkompliziert die Sache ein wenig. Stellt euch vor, irgendwo in unserem Tropfen findet sich in paar Wassermoleküle zusammen und bilden einen winzigkleinen Eiskristall, der nur aus einer Handvoll Moleküle besteht. An der Grenze zwischen unserem Eiskristall und dem flüssigen Wasser drum herum gibt es jetzt ein Problem – die perfekt geordneten Eiskristalle und die drum herum schwimmenden Wassermoleküle passen in der Anordnung nicht optimal zusammen. Die Grenzfläche zwischen beiden ist deshalb energetisch ungünstig. Unser winzig kleiner Eiskristall braucht deshalb auch ein wenig Energie, um sich zu bilden.
Wir haben jetzt also zwei Energien (genau gesagt sind das Freie Energien): Einerseits gewinnen wir Energie, weil der Eiskristall energetisch günstiger ist als das flüssige Wasser, aber wenn der Eiskristall in flüssiges Wasser eingebettet ist, dann brauchen wir auch Energie, um die Grenze zwischen den beiden Bereichen zu bilden. Der erste Energieterm ist proportional zum Volumen unseres Kristalls, der zweite aber zur Oberfläche. Und jetzt kommt eine Beziehung ins Spiel, die auch in ganz anderen Bereichen der Wissenschaft wichtig ist: Das Verhältnis von Oberfläche zu Volumen.
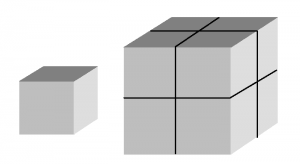
Stellt euch dazu einen kleinen und einen großen Würfel vor, so wie hier:
Wenn ihr den großen Würfel aus acht kleinen zusammensetzt, dann seht ihr, dass viele der Oberflächen der kleinen Würfel Innen landen – der große Würfel hat das achtfache Volumen des kleinen, aber nur die vierfache Oberfläche. Je größer ein Würfel wird, um so kleiner ist seine Oberfläche im Verhältnis zum Volumen. Und das gilt nicht nur für Würfel, sondern für alle denkbaren Formen von Körpern.
Und es gilt auch für unseren kleinen Eiskristall, der gerade versucht, sich zu bilden. Ist er sehr klein, dann hat er eine große Oberfläche im Verhältnis zu seinem Volumen. Die Energie der Grenzfläche ist deswegen groß, so dass der Kristall insgesamt energetisch ungünstig ist. Ist der Kristall dagegen groß, ist seine Oberfläche vergleichsweise klein und er ist energetisch günstig. Ich klaue mal ein Bild bei mir selbst, um das zu erklären:
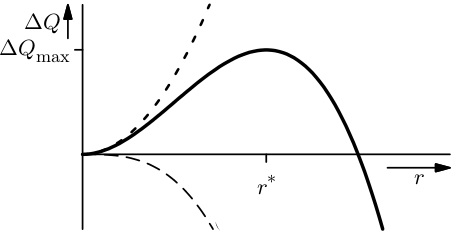
(Leicht verändert aus Rösler, Harders, Bäker “Mechanisches Verhalten der Werkstoffe”, Springer-Vieweg Verlag)
Hier ist auf der horizontalen Achse der Radius des (als kugelförmig angenommenen) Kristalls aufgetragen, auf der senkrechten Achse die Energieänderung gegenüber dem Ausgangszustand. (Eigentlich haben wir das Bild für die Ausscheidung von Teilchen in Metallen gemalt, dazu nachher mehr, aber die Logik ist dieselbe.) Die kurz-gestrichelte Linie (die immer weiter anwächst) gibt die Energieänderung für die Oberflächenenergie an, die langgestrichelte Linie (die nach unten geht) die für den Energiegewinn, weil der Kristall günstiger ist als die Flüssigkeit. Die durchgezogene Linie ist die Summe aus beiden.






Kommentare (19)