Im Moment ist es ja draußen oft kalt und nass, und wenn ich morgens zu meinem Auto gehe, muss ich öfters mal die Scheibe freikratzen. Das ist zwar nervig, aber immerhin kann man sich dabei auch Gedanken über Physik machen. Neulich zum Beispiel war es nachts nur ganz knapp unter den Gefrierpunkt abgekühlt und die Eiskristalle auf der Scheibe waren ziemlich groß. Ein paar Tage vorher war es deutlich kälter und auch relativ trocken – die Schicht auf der Scheibe war sehr dünn und bestand aus kleinen, aber immer noch deutlich erkennbaren Kristallen. Grund genug, mal ein bisschen was über das Wachstum von Kristallen zu schreiben – zumal das auch technisch ein ziemlich wichtiges Thema ist.
Nebenbei: Habt ihr euch eigentlich schon mal gewundert, warum oft nur die Autoscheiben zufrieren, die Karosserie selbst dagegen meist nicht? Und ist euch schon mal aufgefallen, dass die Autoscheiben manchmal zugefroren sind, obwohl es die ganze Zeit knapp oberhalb des Gefrierpunktes war? Der Grund dafür ist, dass die Scheiben eures Autos kälter werden können als die Umgebung – Glas strahlt nämlich Wärme als Infrarotstrahlung ab und kühlt deswegen aus. Es absorbiert auch Infrarotstrahlung aus der Umgebung, aber gerade bei klarem Himmel und einer Scheibe, die schräg nach oben zeigt, bekommt das Glas nur wenig Infrarotstrahlung ab, und der Himmel wirkt wie ein Kühlaggregat. (Aus dem gleichen Grund friert eine Scheibe auch etwas weniger schnell zu, wenn ihr an einer Hauswand steht – die heizt die Scheibe mit ihrer Strahlung auf.) Unsere KollegInnen vom Fraunhoferinstitut hier in Braunschweig haben übrigens auf der Basis dieser Überlegungen eine eisfreie Scheibe entwickelt – leider ist die noch nicht ganz serienreif.
Aber zurück zu Schnee und Eis. Die bilden sich ja, wenn man Wasser unter den Gefrierpunkt abkühlt (wer hätte das gedacht)? Warum ist das eigentlich so? Ein Teil der Antwort ist recht einfach – in festem Wasser (wie in den meisten Festkörpern) sind die einzelnen Bestandteile (die Wassermoleküle) schön regelmäßig angeordnet. Hier ein schickes Bild dazu:

“Cryst struct ice” by Solid State – own drawing, created with Diamond 3.1. Licensed under CC BY-SA 3.0 via Wikimedia Commons.
Das Blaue sind die Sauerstoff-Atome (“O”) und das Weiße die Wasserstoff-Atome (“H”). Die dicken durchgezogenen Linien sind die “normalen” Atombindungen, die gestrichelten Linien sind die Wasserstoffbrücken, über die Florian neulich schon etwas geschrieben hat. Die chemisch-physikalischen Details sind mir heute egal (obwohl Wasserstoffbrücken ziemlich interessante Dinger sind), hier ist nur wichtig, dass ihr seht, dass die Anordnung schön regelmäßig ist. Das ist energetisch günstig, und deshalb bilden sich diese Strukturen dann, wenn wenig Energie zur Verfügung steht (also bei niedrigen Temperaturen).
Bei höheren Temperaturen werden die Moleküle aber immer unruhiger – Wärme ist ja nichts anderes als die Bewegung von Atomen und Molekülen, je wärmer es also wird, desto “zappeliger” werden die Moleküle auch. Erreicht man – unter Normalbedingungen – eine Temperatur von 0°, dann schmilzt das Eis und wird flüssig – die Moleküle ordnen sich jetzt ständig um und sitzen nicht mehr sauber im Kristallgitter. Wenn man genau hinguckt, sieht man aber, dass die Moleküle immer noch über die Wasserstoffbrücken zusammenhalten; die Verbindungen werden aber immer wieder gelöst und dann neu geknüpft.
Betreibt man theoretische Physik und verwendet die Methoden der Thermodynamik, dann stellt man fest, dass die Umwandlung vom festen zum Flüssigen Zustand bei einer ganz bestimmten Temperatur passiert – unter normalen Bedingungen sind das eben die 0°C. (Warum das so ist, habe ich vor langer Zeit mal erklärt.) Aber jetzt tue ich etwas für mich sehr ungewöhnliches und gebe zu, dass die theoretische Physik (jedenfalls in dieser einfachen Form) nicht alles ist. Die Berechnungen aus der Thermodynamik funktionieren so nämlich nur, wenn man unendlich große Systeme hat in denen sich die Temperatur unendlich langsam ändert. Die Winternächte, in denen meine Autoscheibe zufriert, sind zwar lang, aber so lang nun auch wieder nicht.
Stellt euch also einen Wassertropfen vor (oder für den Frost auf der Scheibe den in der Luft gelösten Wasserdampf, aber ich bleibe mal beim Tropfen, die Logik ist dieselbe), den ihr abkühlt. Wenn ihr genau Null Grad erreicht, dann sollte der Tropfen eigentlich gefrieren (weil das energetisch günstiger ist (oder noch genauer gesagt – siehe den oben verlinkten Artikel und die zugehörige Serie, die ihr rechts unter Artikelserien findet – weil die Freie Energie des festen Zustandes dann kleiner ist als die des flüssigen Zustands.)) Wenn ihr die Temperatur eine Winzigkeit unter Null Grad absenkt, dann ist aber der Gewinn, den ihr habt, auch nur sehr klein. Mit anderen Worten: Die treibende Kraft für den Prozess (wobei man sich unter Kraft jetzt nicht das vorstellen sollte, was man in der Mechanik mal in der Schule gelernt hat, sondern einfach den Energiegewinn, der den prozess antreibt) ist sehr klein. Das ist auch genau der Grund, warum man in der Theorie unendlich lange warten muss – dann setzt sich auch der unendlich kleine Vorteil schließlich durch.
In einem realen Wassertropfen geht die Umwandlung aber natürlich an irgendeinem Punkt los und breitet sich von dort aus – der ganze Wassertropfen erstarrt nicht schlagartig zu Eis. Und das verkompliziert die Sache ein wenig. Stellt euch vor, irgendwo in unserem Tropfen findet sich in paar Wassermoleküle zusammen und bilden einen winzigkleinen Eiskristall, der nur aus einer Handvoll Moleküle besteht. An der Grenze zwischen unserem Eiskristall und dem flüssigen Wasser drum herum gibt es jetzt ein Problem – die perfekt geordneten Eiskristalle und die drum herum schwimmenden Wassermoleküle passen in der Anordnung nicht optimal zusammen. Die Grenzfläche zwischen beiden ist deshalb energetisch ungünstig. Unser winzig kleiner Eiskristall braucht deshalb auch ein wenig Energie, um sich zu bilden.
Wir haben jetzt also zwei Energien (genau gesagt sind das Freie Energien): Einerseits gewinnen wir Energie, weil der Eiskristall energetisch günstiger ist als das flüssige Wasser, aber wenn der Eiskristall in flüssiges Wasser eingebettet ist, dann brauchen wir auch Energie, um die Grenze zwischen den beiden Bereichen zu bilden. Der erste Energieterm ist proportional zum Volumen unseres Kristalls, der zweite aber zur Oberfläche. Und jetzt kommt eine Beziehung ins Spiel, die auch in ganz anderen Bereichen der Wissenschaft wichtig ist: Das Verhältnis von Oberfläche zu Volumen.
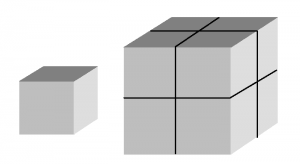
Stellt euch dazu einen kleinen und einen großen Würfel vor, so wie hier:
Wenn ihr den großen Würfel aus acht kleinen zusammensetzt, dann seht ihr, dass viele der Oberflächen der kleinen Würfel Innen landen – der große Würfel hat das achtfache Volumen des kleinen, aber nur die vierfache Oberfläche. Je größer ein Würfel wird, um so kleiner ist seine Oberfläche im Verhältnis zum Volumen. Und das gilt nicht nur für Würfel, sondern für alle denkbaren Formen von Körpern.
Und es gilt auch für unseren kleinen Eiskristall, der gerade versucht, sich zu bilden. Ist er sehr klein, dann hat er eine große Oberfläche im Verhältnis zu seinem Volumen. Die Energie der Grenzfläche ist deswegen groß, so dass der Kristall insgesamt energetisch ungünstig ist. Ist der Kristall dagegen groß, ist seine Oberfläche vergleichsweise klein und er ist energetisch günstig. Ich klaue mal ein Bild bei mir selbst, um das zu erklären:
(Leicht verändert aus Rösler, Harders, Bäker “Mechanisches Verhalten der Werkstoffe”, Springer-Vieweg Verlag)
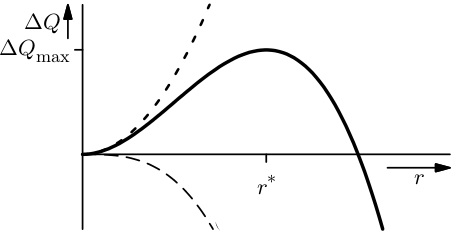
Hier ist auf der horizontalen Achse der Radius des (als kugelförmig angenommenen) Kristalls aufgetragen, auf der senkrechten Achse die Energieänderung gegenüber dem Ausgangszustand. (Eigentlich haben wir das Bild für die Ausscheidung von Teilchen in Metallen gemalt, dazu nachher mehr, aber die Logik ist dieselbe.) Die kurz-gestrichelte Linie (die immer weiter anwächst) gibt die Energieänderung für die Oberflächenenergie an, die langgestrichelte Linie (die nach unten geht) die für den Energiegewinn, weil der Kristall günstiger ist als die Flüssigkeit. Die durchgezogene Linie ist die Summe aus beiden.
Wie groß muss ein Kristall sein, damit er weiter wachsen kann? Im ersten Moment könnte man versucht sein, zu sagen, dass er so groß sein muss, dass seine Energie insgesamt kleiner ist als die des rein flüssigen Ausgangszustands – das wäre der Punkt, wo die Kurve die horizontale Achse schneidet. Das ist jedoch nicht richtig. Wenn sich nämlich erst einmal ein Teilchen gebildet hat, dessen Radius so groß ist, dass das Maximum der Kurve überschritten ist, dann kann das Teilchen ja unter Energiegewinn weiterwachsen. Es muss sich also mindestens ein Teilchen mit Radius r* bilden.
Weil sich aber meist nicht spontan einige Hundert, Tausend oder noch mehr Wassermoleküle zu Eis zusammenfinden, kann man Wasser auch unter 0°C abkühlen, ohne dass es gefriert. Man hat dann unterkühltes Wasser. Eiskristalle bilden sich dann meist an Stellen, wo das energetisch günstig ist, beispielsweise Staubteilchen oder Kratzer an einer glatten Oberfläche. (Beim Regen ist das übrigens ganz ähnlich, auch da kondensieren Tropfen nach der gleichen Logik, und auch das tun sie bevorzugt an irgendwelchen Staubteilchen oder ähnlichem, das in der Luft herumschwebt.) Solche günstigen Stellen und die kleinen Kristalle, die sich dort bilden, heißen auch Kristallisationskeime.
Hat man sehr reines Wasser in einem hinreichend glatten Gefäß, kann man es auch sehr stark unterkühlen. Dann reicht schon eine kleine Erschütterung, um genügend Energie zur Verfügung zu stellen, damit das Wasser gefriert. Dieses Video zeigt das sehr schön (ich empfehle, den Ton auszuschalten, es sei denn, ihr habt einen seeeehr seltsamen “Musik”-Geschmack (das Wort “Musik” kann man hier wirklich nur in weitestem Sinne verwenden…))
Den gleichen Trick verwenden auch Wärme-Packs – sie enthalten ein Poymer ein Salz (dank an Sebastian für die Korrektur), dass massiv unterkühlt ist und das ihr durch Knipsen eines Metallclips zum Gefrieren bringen könnt. Dabei wird Energie frei, die dann eure Hände wärmt.
Wenn ihr noch einmal auf das Bild oben schaut, in dem ich den Radius r* erklärt habe, der bestimmt, ab wann ein Keim wachsen kann, dann seht ihr, dass die Größe von r* natürlich davon abhängt, wie groß die beiden Energieterme relativ zueinander sind. Gewinne ich nur wenig Energie beim gefrieren, dann verläuft die untere Kurve (die proportional zum Volumen ist) sehr flach und r* ist sehr groß; gewinne ich viel Energie, dann ist r* entsprechend klein.
Und das ist jetzt genau der Grund, warum Eiskristalle verschieden groß sind, je nachdem, bei welcher Temperatur sie sich bilden. Der Gewinn an (freier) Energie ist direkt unter dem Gefrierpunkt sehr klein, sehr weit unter dem Gefrierpunkt groß. Direkt unter dem Gefrierpunkt brauche ich also extrem günstige Kristallisationskeime, damit die groß genug sind und wachsen können. Davon gibt es nur wenige, deswegen bekomme ich wenige große Kristalle. Weit unter dem Gefrierpunkt dagegen reicht auch schon ein kleiner Kristallisationskeim, so dass ich viele kleine Keime bekomme.
Beim Eis auf meiner Autoscheibe kommt allerdings auch hinzu, wie viel Wasserdampf in der Luft gelöst ist – auch das hat einen Einfluss auf dei treibende Kraft. Ähnlich ist es auch beim Schnee – für die Form und Größe von Schneeflocken spielt nicht nur eine Rolle, wie stark der Wasserdampf in der Luft unterkühlt ist, sondern auch, wie viel Wasserdampf in der Luft ist, wie stark die Luft also mit Wasser übersättigt ist. Weil dieser Artikel eh schon recht lang ist (und ich auch noch was über Metalle schreiben wollte), verweise ich für Details mal auf diese Seite hier , dort findet ihr auch noch einen link auf ein ziemlich ausführliches (aber auch nicht ganz einfaches) Paper zum Thema. Zum Wachsen von Schnneflocken empfehle ich auch diese Videos hier.
Schneeflocken und Eiskristalle sind ohne Frage hübsch und auch sicher nicht ganz unwichtig – aber das Prinzip des Kristallwachstums spielt auch in der Technik eine große Rolle. Um zu verstehen, wie das geht, müssen wir ganz kurz gucken, wie Metalle sich verformen (ausführlicher habe ich das hier erklärt): In Metallen gibt es Fehlstellen (so genannte Versetzungen), die sich durch den Kristall bewegen und dabei einen Teil des Materials gegen den Rest abscheren. Ein Bild einer Versetzung seht ihr übrigens oben in meinem Logo rechts in der Mitte. Um Metalle an der Verformung zu hindern, muss man deshalb die Versetzungen in ihrer Bewegung behindern (manchmal kann man das mit Nichts tun).
Kühlt man ein Metall aus der Schmelze ab, dann bilden sich einzelne Kristalle, ganz ähnlich wie beim Eis. Beim Metall heißen diese Kristalle Körner und sehen so aus:
(Aus Rösler, Harders, Bäker “Mechanisches Verhalten der Werkstoffe”, Springer-Vieweg Verlag)
Manchmal sind diese Körner auch sehr groß, dann kann man sie direkt mit bloßem Auge sehen, beispielsweise bei Laternenmasten.
Verformt man ein Metall bei Raumtemperatur, dann sind die Grenzen zwischen den Körnern Hindernisse für Versetzungen, man möchte also für ein besonders festes Metall kleine Körner haben. Wie groß die Körner beim Erstarren aus der Schmelze sind, hängt davon ab, wie man den Abkühlvorgang genau steuert – aber weil die involvierten Temperaturen sehr hoch sind, nutzt man zum Einstellen der Korngröße oft einen anderen Trick.
Als erstes verformt man das Metall stark, beispielsweise durch einen Walzprozess. Dabei bewegen sich die Versetzungen, zusätzlich entstehen aber auch viele neue Versetzungen im Material, die das Kristallgitter ziemlich durcheinanderwürfeln. Dadurch ist jetzt sehr viel Energie im Metall gespeichert. Wenn man das Metall jetzt erwärmt, dann ist es energetisch günstiger, wenn sich die Atome umsortieren und neue Körner mit wenig Versetzungen drin ausbilden. Weil sich die Kristalle neu bilden, heißt das auch Rekristallisation. Wie groß die Körner sind, die sich neu bilden, hängt wieder davon ab, wie groß die treibende Kraft (der Gewinn durch die Energie im Volumen) gegenüber der Oberflächenenergie (denn es bilden sich ja neue Grenzen zwischen Körnern, die Energie kosten) ist. Hier ist es jetzt vor allem die Größe der gespeicherten Energie, die entscheidend ist – habt ihr das Material nur moderat stark gewalzt, ist nicht so viel Energie gespeichert, und nur sehr günstige Anfangskeime können wachsen. Entsprechend bekommt ihr wenige große Körner. Habt Ihr das Material dagegen heftig umgeknetet, dann ist sehr viel Energie gespeichert und die Körner sind klein (was für Anwendungen bei Raumtemperatur gewünscht ist).
Es gibt aber auch einen entscheidenden Unterschied zu unseren Eiskristallen: Dort reichen sehr kleine Keime, die sich auch spontan bilden können. Bei der Rekristallisation ist das anders – die notwendige Keimgröße liegt im Bereich von Mikrometern. Das Wachstum beginnt deshalb an Stellen, an denen die Atome schon halbwegs passend zur neuen kristallstruktur angeordnet sind (zum Beispiel an den Korngrenzen). Wikipedia hat dazu deutlich mehr Infos.
Eine andere Möglichkeit, um Metalle zu verfestigen, sind Ausscheidungen (nein, nicht die Art von Ausscheidungen (Igitt, was ihr immer denkt…)). Ausscheidungen in Metallen sind kleine Teilchen innerhalb der Körner, die eine andere Zusammensetzung haben.
Im Aluminiumlegierungen beispielsweise kann man etwas Kupfer zulegieren. Dann können sich kleine Kupfer-Aluminium-Teilchen bilden, die die Versetzungsbewegung stören und das Material wesentlich fester machen.So sehen diese Teilchen (jedenfalls, wenn sie sehr klein sind) aus:
(By User A1 at en.wikipedia [GFDL or CC-BY-SA-3.0], from Wikimedia Commons)
Fragt sich nur, wie man die kleinen fein verteilten Teilchen in das Material reinbekommt. Dazu nutzt man die gleiche Logik wie bei unseren Eiskristallen: Bei hoher Temperatur löst sich Kupfer in Aluminium sehr gut. Kühlt man jetzt schnell auf Raumtemperatur ab, dann bleiben die Kupferatome im Kristallgitter – eigentlich wäre es für sie energetisch günstig, wenn sie sich zu Kupfer-Aluminium-Teilchen zusammenfinden würden, aber bei Raumtemperatur sind die Teilchen einfach nicht sehr beweglich. Wenn man die Legierung jetzt wieder etwas erwärmt, dann werden die Teilchen beweglicher und es können sich die entsprechenden Teilchen aus dem Kristall ausscheiden (deswegen heißt das so). Erhöht man die Temperatur sehr stark, dann sind die Kupfer-Atome zum einen recht beweglich und zum anderen ist die treibende Kraft, um Ausscheidungen zu bilden, recht klein – in dem Fall bekommt man also wenige, große Ausscheidungen. Bei niedrigerer Temperatur gibt es mehr Ausscheidungen, die dafür kleiner sind. Da es eine optimale Ausscheidungsgröße gibt, bei der die Teilchen die Versetzungen maximal behindern und so für die größte Festigkeit sorgen, kann man durch genaues Einstellen der Temperatur, bei der der Prozess stattfindet, auch die optimale Größe einstellen. (Wenn ihr mehr darüber wissen wollt, dann empfehle ich das oben schon erwähnte Buch “Mechanisches Verhalten der Werkstoffe”.)
Ihr seht, dass die Physik des Kristallwachstums uns eigentlich ziemlich häufig begegnet. Auch wenn die Einzelheiten oft kompliziert sind (und ich habe hier einiges deutlich vereinfacht…), ist das Prinzip doch meist dasselbe: Neue Teilchen zu bilden, kostet Energie an der Oberfläche, bringt aber im Volumen einen Energiegewinn, und wie diese beiden Energien miteinander streiten, entscheidet darüber, ob ihr große oder kleine Kristalle von eurer Autoscheibe kratzen müsst.








Kommentare (19)