Damit können wir das Bild der Raumkrümmung jetzt auf unser Universum übertragen: Das Universum als ganzes kann eine Krümmung haben, so wie die Erdoberfläche (oder die Ebene). Zusätzlich gibt es auch noch lokal Bereiche mit unterschiedlicher Krümmung. Wir können uns den Raum als gekrümmt vorstellen – wir können aber genauso gut so tun, als wäre der Raum ein ganz gewöhnlicher flacher Raum, auf dem allerdings an unterschiedlichen Punkten ein spezielles Feld (so wie unser Temperaturfeld) die Maßstäbe aller Objekte verzerrt. Dieses Bild funktioniert nur dann, wenn alle Objekte genau gleich beeinflusst werden (wenn es in der zweidimensionalen Welt ein Objekt gibt, das sich nicht mit der Temperatur ausdehnt, dann könnt ihr mit dessen Hilfe sehen, dass sich Maßstäbe von Ort zu Ort ändern.). Genau das ist aber in der ART der Fall – letztlich ist das die Aussage des berühmten Äquivalenzprinzips, das besagt, dass alle Objekte in einem Schwerefeld gleich schnell fallen.
Die Raumkrümmung in unserem Universum ist allerdings nicht statisch, wie in unserer zweidimensionalen Modellwelt, sondern sie ist dynamisch – sie kann sich mit der Zeit ändern. Auch das können wir uns aber in unserem Modell leicht vorstellen: stellt euch beispielsweise vor, ihr würdet an einer Stelle der Platte einen Eiswürfel auflegen, dann wird die Temperatur dort niedriger – es entsteht also ein “Berg” in unserer Welt.
Auch die Ausdehnung des Universums lässt sich in unser Modell übertragen – dazu müssen wir nur die Temperatur im Laufe der Zeit immer weiter absenken – dann “schrumpfen” die Objekte in unserem Universum, also vergrößern sich die Abstände zwischen ihnen (weil ja auch die Maßstäbe mitschrumpfen). Im Modell der Kugeloberfläche dagegen lassen wir die Kugel wachsen, so wie man einen Ballon aufbläst (was ja ein beliebtes Bild für das Expandieren des Universums ist.)
Man kann den Raum also so beschreiben, als sei er gekrümmt – man kann aber genauso gut stattdessen annehmen, dass es einen zu Grunde liegenden Raum gibt (den wir allerdings nicht direkt beobachten können), der von einem “Feld” erfüllt ist (wie unserem Temperaturfeld), das alle Materie in der gleichen Weise beeinflusst (insbesondere lässt es Maßstäbe schrumpfen oder wachsen). Dieses Feld können wir dann “Gravitationsfeld” nennen.
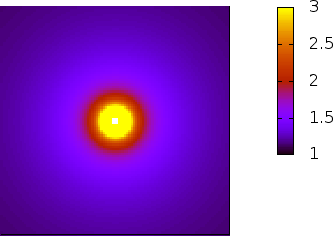
Stellt euch vor, ihr habt eine Masse, die um sich herum den Raum verzerrt. In einer zweidimensionalen Darstellung könnt ihr das genau so über die Veränderung des Maßstabs (also der Temperatur) darstellen, wie wir es oben für die Kugeloberfläche gemacht haben. So sieht das Ergebnis aus:
Die absoluten Zahlen sind dabei vollkommen willkürlich, lediglich das Verhältnis zueinander ist relevant. (Nochmal herzlichen Dank an Dieter für diesen erhellenden Kommentar.)
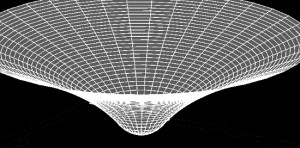
Ihr könnt euch aber auch einen gekrümmten Raum vorstellen, dort sähe das Ganze etwa so aus (wenn man den gekrümmten Raum in den dreidimensionalen Raum einbettet):
(Ausführlich habe ich dieses Bild und was es bedeutet hier erklärt). Hinweis für die Expertinnen: Die erste Darstellung verwendet isotrope Koordinaten, die zweite Schwarzschild-Koordinaten. Die Radialkoordinate ist in den beiden Bildern nicht identisch, man kann sie nicht einfach übereinander legen und direkt vergleichen. Das sieht man auch daran, dass der Weg nach Innen bei Schwarzschild-Koordinate ja immer länger wird, während in isotropen Koordinaten die Maßstäbe nach innen hin größer werden, nicht kleiner. Und noch ein Hinweis: In den Feynman Lectures sagt Feynman, dass sich die Raumkrümmung durch einen einzigen Skalenfaktor an jedem Punkt darstellen lässt. Das hat mich immer verwirrt, weil man zur Angabe der Metrik an jedem Punkt ja mehr als eine Zahl braucht, während ein Skalenfaktor nur eine Zahl ist. Das Beispiel mit den Landkarten zeigt aber, dass das täuscht, weil nicht jede Projektion für eine winkeltreue Darstellung sorgt – man muss die Abstände der Längen- und Breitengrade genau so wählen, wie Mercator das in seiner Projektion tut. Entsprechend lässt sich eine Darstellung mit einer einzigen Zahl eben nicht in jedem beliebigen Koordinatensystem realisieren, sondern nur in einem geeignet gebastelten. (Mal wieder ein Beispiel dafür, dass die Feynman Lectures zwar toll sind, dass aber vieles leider ungesagt bleibt und einen manchmal etwas hilflos zurücklässt.)






Kommentare (81)