Ich grabe hier mal meine alten Warnschilder aus, für alle, die sich von Formeln nicht abschrecken lassen. Der Energie-Impuls-Tensor so eines Fluids ist laut Wikipedia:
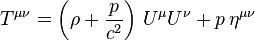
U ist die Geschwindigkeit, p der Druck, ρ die Dichte.
Die Gravitation hat also einen Einfluss auf die Geschwindigkeit und den Druck der Flüssigkeit.
In so einer Flüssigkeit können sich ja beispielsweise Dichtewellen ausbreiten, die nichts anderes sind als Schallwellen. Und insofern ist es – ohne dass ich das jetzt im einzelnen nachgerechnet habe – hoffentlich plausibel, dass ein Gravitationsfeld natürlich einen Einfluss auf die Geschwindigkeit so einer Welle und auf ihre Wellenlänge haben kann. Wenn wir also unsere Welle als Maßstab nehmen und beispielsweise die Frequenz der Welle verwenden, um unsere Zeiteinheit zu definieren, dann wird diese Zeiteinheit sich bei Anwesenheit eines Gravitationsfeldes ändern; nehmen wir die Wellenlänge als Maßstab für den Raum, ändert sich der entsprechend auch.
Allgemein gesagt können wir dem Beispiel folgende Idee entnehmen: Das Gravitationsfeld wechselwirkt mit der Energie, dem Impuls und der Spannung eines Systems. Diese Größen hängen alle nicht nur von den Werten des Systems an einem Punkt ab, sondern davon, wie sich die Werte räumlich oder zeitlich ändern. (Die kinetische Energie und der Massenstrom haben zum Beispiel etwas mit der Geschwindigkeit zu tun, also mit einer zeitlichen Änderung.) Entsprechend hat das Gravitationsfeld auch einen Einfluss auf die räumliche und zeitliche Änderung und damit darauf, wie schnell oder in welchem Abstand Dinge sich ändern.
Wenn wir noch etwas genauer hingucken, dann können wir das auch an einer Größe festmachen, die in der Physik gern verwendet wird, nämlich der Wirkung. Die Wirkung ist eine Größe, die die kinetische und potentielle Energie eines Systems enthält. In der klassischen Physik gibt es das Prinzip der kleinsten Wirkung, das besagt, dass die Wirkung minimal wird. (Achtung, der Begriff “Wirkung” ist ziemlich unglücklich gewählt, das Prinzip besagt nicht, dass die Natur irgendwie besonders ökonomisch ist und alles möglichst effizient passiert oder so. Dass die Größe Wirkung heißt, ist im wesentlichen ein historischer Zufall.) Wen sich also zum Beispiel eine Welle mit einer bestimmten Wellenlänge oder Geschwindigkeit ausbreitet, dann tut sie das so, dass die Wirkung minimiert wird.
Haben wir ein Gravitationsfeld, dann geht dessen Einfluss direkt in die Wirkung ein. Meist interpretiert man das direkt über die Raum-Zeit-Krümmung und sagt, dass wir in der Wirkung (wo eben räumliche und zeitliche Änderungen drinstecken) berücksichtigen müssen, dass die Raumzeit gekrümmt ist. Wir können den entsprechenden Term aber genauso gut als Feld interpretieren und sagen, dass dieses Feld mit dem Rest unseres Systems wechselwirkt. Tatsächlich sieht das mathematisch ganz ähnlich aus zu der Wechselwirkung zwischen dem elektromagnetischen Feld und einem System, das elektrische Ladungen enthält. Insofern können wir den Einfluss der Gravitation also auch als Feld beschreiben.
Ist die Gravitation ein Feld wie jedes andere?
Im Feldbild scheint also an der Gravitation nicht viel besonderes zu sein. Ist die Gravitation also ein ganz gewöhnliches Feld genau wie das elektromagnetische Feld? Das könnte man jetzt in der Tat denken – und Einstein hat viele Jahre seines Lebens damit verbracht, andersherum zu versuchen, das elektromagnetische Feld mit einer Raumzeitkrümmung oder etwas ähnlichem in Verbindung zubringen. Warum geht das nicht? Was ist das Besondere am Gravitationsfeld?
Das elektromagnetische Feld wirkt nicht auf alle Materie – es gibt Materie, die geladen ist, und solche, die es nicht ist. Unterschiedliche Teilchen können unterschiedlich stark geladen sein, und reagieren dann auch unterschiedlich auf ein elektrisches Feld. Wenn ich zum Beispiel zwei Eisenatome habe und den einen eins, dem anderen zwei Elektronen klaue, so dass ich einfach oder zweifach ionisiertes Eisen bekomme, dann werden die beiden Eisenatome unterschiedlich stark im elektrischen Feld beschleunigt, denn das zweifach ionisierte Eisenatome erfährt die doppelte Kraft, hat aber dieselbe Masse.
Kommentare (128)