Im Moment beschäftige ich mich ja mit der Krümmung von Raum und Zeit, also der Allgemeinen Relativitätstheorie (ART). In den ersten beiden Teilen haben wir gesehen, dass man sich die Raumkrümung alternativ auch mit Hilfe eines Gravitationsfeldes veranschaulichen kann, weil das feld Maßstäbe verzerrt. Aber wie ist es mit der Zeit? Dass ein Feld eine Art Kraft ausübt und damit Maßstäbe verzerren kann, lässt sich ja noch irgendwie vorstellen. Aber wie schafft es ein Feld, die Zeit zu beeinflussen?
Anmerkung: Ich habe mir beim Schreiben dieses Artikels (den ich schon vor zwei Wochen angefangen habe) erst mal ein paar Gedanken gemacht, die nicht ganz zielführend sind. Ich lasse die hier einfach mal stehen; vielleicht ist es ja ganz interessant zu sehen, wie sich meine Gedanken entwickelt haben. Wenn euch das nicht interessiert, könnt ihr zum Abschnitt “Nochmal ganz anders” weiterspringen.
Erste Gedanken
Im Rahmen der speziellen Relativitätstheorie ist die Sache eigentlich ganz einfach: Unterschiedliche Beobachterinnen (*) nehmen Raum und Zeit unterschiedlich wahr – euer Raum wird (zumindest teilweise) zu meiner Zeit und umgekehrt (Ereignisse, die für euch gleichzeitig in großer Entfernung stattfinden, sind für mich nicht gleichzeitig, aber dichter benachbart). Wenn ein Feld also den Abstand zwischen Dingen beeinflussen kann, dann muss es auch den Zeitablauf dieser Dinge beeinflussen können. (Tatsächlich ist es mehr oder weniger Standard, die Gleichungen der ART unter anderem dadurch zu motivieren, dass man den klassischen Grenzfall einer stillstehenden Masse nach Newton verwendet und dann überlegt, wie diese Gleichung in unterschiedlichen Bezugssystemen aussieht – so legt zum Beispiel das Buch von Misner Thorne Wheeler die Proportionalitätskonstante zwischen Einstein-Tensor und Energie-Impuls-Tensor fest.)
*Ja, wie beim letzten Mal mit “generischem” Femininum – alle, die sich darüber aufregen wollen, klicken heute hier.
So richtig befriedigend ist das aber natürlich nicht, auch wenn es vom physikalischen Standpunkt aus natürlich eine ziemlich wasserdichte Herleitung ist – immerhin ist die spezielle Relativitätstheorie verdammt gut bestätigt. Zumindest ein bisschen würde man gern eine Anschauung bekommen, warum sich Zeiten ändern sollen.
In einem Gravitationsfeld gehen Uhren langsamer als weit von diesem Feld entfernt. Das ist eine Folgerung aus der ART, die auch experimentell gut bestätigt ist. Wie sorgt nun also ein Feld dafür, dass eine Uhr langsamer geht?
Eine Möglichkeit, sich das zu überlegen, ist, sich eine konkrete Uhr anzugucken. Am besten nicht gerade die Uhr mit dem Pendel aus eurem Wohnzimmer – die verwendet ja schon die Schwerkraft, um die Zeit zu messen, da wird es dann schwierig zu sehen, welchen Einfluss ein Schwerefeld auf die Uhr haben soll. Wir können aber ja zum Beispiel eine Atomuhr nehmen. Technisch werden meistens Cäsium oder Rubidium verwendet, es geht aber auch mit Wasserstoffatomen. Wird ein Wasserstoffatom energetisch angeregt, so wird ein Elektron in einen Zustand höherer Energie gehoben. Beim Zurückfallen in den Grundzustand sendet es dann Licht mit einer charakteristischen Frequenz aus. Diese Frequenz (die Zahl der Schwingungen der Lichtwelle pro Sekunde) können wir nehmen, um eine Uhr zu konstruieren.
Das Feld, das den Raum verzerrt, beeinflusst auch das elektrische Feld des Atomkerns. Zusätzlich hat ein Elektron in einem Schwerefeld eine etwas kleinere Energie als außerhalb (Dinge gewinnen ja Energie, wenn sie nach unten fallen). Da Energie und Masse zusammenhängen, ändert sich im Schwerefeld also auch die Masse eines Elektrons. Mit diesen Überlegungen lässt sich ausrechnen, dass sich die charakteristische Frequenz des Wasserstoffatoms ändert, und zwar genau so, wie es der Zeitdilatation nach der ART entspricht.
Expertinnenhinweis: Die detaillierte Rechnung findet man in diesem paper. Ich muss allerdings zugeben, dass mir einiges nicht klar ist – insbesondere habe ich keinen Schimmer, von welchem Himmel die Gleichung (41) fällt und warum die effektive Masse des Elektrons im Schwerefeld größer sein soll als außerhalb. Falls jemand das durchschaut, hinterlasst einen Kommentar.
Aber so richtig befriedigend ist das immer noch nicht, oder?
Anmerkung: Das hier war dann der Moment, wo ich noch einmal über die räumliche Verzerrung nachgedacht habe – das Ergebnis dieser Überlegungen wurde dann der zweite Teil des Artikels, der also nach dem entstand, was ich hier geschrieben habe.
Probleme, Probleme, Probleme
Hmm, wenn ich ehrlich bin, habe ich es mir bisher zu einfach gemacht. Die Vorstellung, dass ein Gravitationsfeld räumliche Maßstäbe verändern kann (so wie im zweiten Teil beschrieben), habe ich mir in Analogie zur thermischen Ausdehnung gebildet. Aber thermische Ausdehung ist ein ziemlich kompliziertes Phänomen (hey, darüber könnte ich auch mal bloggen), das letztlich darauf beruht, dass die Energie-Kurve für die Bindung zwischen Atomen asymmetrisch verläuft (etwas unsauber gesagt: es kostet mehr Energie, den Abstand zwischen zwei Atmen ein – nicht infinitesimales – Stück zu verringern als ihn zu erhöhen; wenn man thermische Energie zufügt, sind deshalb große Abstände etwas wahrscheinlicher als kleine).
Aber auf fundamentaler Ebene ist das nicht wirklich hilfreich, oder? Kristalle mit Atombindungen sind schon ziemlich komplizierte Gebilde, und die thermische Ausdehnung taugt sicher nicht besonders als Muster für etwas so Fundamentales wie die Gravitation. Auch die Vorstellung, dass die Gravitation die Dinge irgendwie “zusammenquetscht” und dadurch Abstände beeinflusst, ist problematisch, weil man sich ja auch in einem starken Gravitationsfeld im freien Fall befinden kann und vom Feld nichts merkt (solange man klein genug ist, dass keine Gezeitenkräfte wirken, die also an den Füßen stärker ziehen als am Kopf).
Toll, jetzt sind wir wieder am Anfang, und ich habe gerade die schöne Anschauung kaputt gemacht, die für die räumliche Maßstabsänderung zuständig war. Also zurück zum Start.
Noch mal ganz anders
Fangen wir nochmal ganz fundamental an. Die Schwerkraft (ob als Feld oder als Raumzeitkrümung vorgestellt) hat etwas mit der Masse zu tun. Aber nicht nur. Zunächst mal wissen wir, dass – wegen E=mc² – jede Masse einer Energie äquivalent ist, und auch Teilchen, die keine Ruhemasse haben, reagieren auf Schwerefelder und erzeugen sie. (Falls ihr eine Auffrischung in Sachen Masse und Ruhemasse braucht, findet ihr sie hier.) Also muss die Schwerkraft etwas mit der Energie zu tun haben, nicht bloß mit der Ruhemasse.
Tatsächlich zeigen die Gleichungen der ART, dass die Raumkrümmung nicht nur mit der Energiedichte zusammenhängt, sondern mit dem so genannten Energie-Impuls-Tensor. In dem steckt neben der Energie eines Systems auch noch der Impuls drin (also der Massestrom) sowie der Druck und die Spannung im System. Ich nehme das hier mal als gegeben an – vielleicht schreibe ich irgendwann noch mal extra was zum Energie-Impuls-Tensor. (Ein Problem dabei ist, dass mich immer, wenn ich darüber etwas lese, über das Wort Impulsstromdichte stolpere, dann stoße ich auf irgendwelche Links zum sogenannten “Karlsruher Physikkurs” (der in Wahrheit ein Pseudophysikkurs ist), was dann zu endloser Aufregung führt. Aber das ist wieder ein ganz anderes Thema. Falls ihr darüber diskutieren wollt, dann hinterlasst bitte einen kurzen (!) Kommentar und ich mache einen Extra-Thread dafür auf.)
Nehmen wir mal ein einfaches (und bei Rechnungen der ART beliebtes) Beispiel: Ein ideale Flüssigkeit, also eine Flüssigkeit, in der es keine Reibung gibt. Wir stellen uns vor, dass das Schwerefeld, in dem sich die Flüssigkeit bewegt, sehr stark ist (oder die Flüssigkeit eine sehr geringe Dichte hat), so dass die Flüssigkeit am Schwerefeld nichts wesentliches ändert.
Wie wirkt das Schwerefeld in diesem Fall auf die Flüssigkeit? Zum einen hat die eine Massendichte, auf die das Gravitationsfeld (wir stellen es uns ja als Feld vor, nicht als Raumzeitkrümmung) wirkt. Dann gibt es noch die kinetische Energie der Flüssigkeit, die von der Geschwindigkeit abhängt. Auch auf die wird sich das Gravitationsfeld auswirken. Wenn sich die Flüssigkeit bewegt, haben wir dann auch noch einen Massestrom, der vom Schwerefeld beeinflusst wird, und schließlich hat so eine Flüssigkeit auch noch einen Druck (und wenn wir sie zusammendrücken, erhöhen wir die Dichte).
 Ich grabe hier mal meine alten Warnschilder aus, für alle, die sich von Formeln nicht abschrecken lassen. Der Energie-Impuls-Tensor so eines Fluids ist laut Wikipedia:
Ich grabe hier mal meine alten Warnschilder aus, für alle, die sich von Formeln nicht abschrecken lassen. Der Energie-Impuls-Tensor so eines Fluids ist laut Wikipedia:
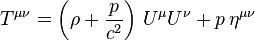
U ist die Geschwindigkeit, p der Druck, ρ die Dichte.
Die Gravitation hat also einen Einfluss auf die Geschwindigkeit und den Druck der Flüssigkeit.
In so einer Flüssigkeit können sich ja beispielsweise Dichtewellen ausbreiten, die nichts anderes sind als Schallwellen. Und insofern ist es – ohne dass ich das jetzt im einzelnen nachgerechnet habe – hoffentlich plausibel, dass ein Gravitationsfeld natürlich einen Einfluss auf die Geschwindigkeit so einer Welle und auf ihre Wellenlänge haben kann. Wenn wir also unsere Welle als Maßstab nehmen und beispielsweise die Frequenz der Welle verwenden, um unsere Zeiteinheit zu definieren, dann wird diese Zeiteinheit sich bei Anwesenheit eines Gravitationsfeldes ändern; nehmen wir die Wellenlänge als Maßstab für den Raum, ändert sich der entsprechend auch.
Allgemein gesagt können wir dem Beispiel folgende Idee entnehmen: Das Gravitationsfeld wechselwirkt mit der Energie, dem Impuls und der Spannung eines Systems. Diese Größen hängen alle nicht nur von den Werten des Systems an einem Punkt ab, sondern davon, wie sich die Werte räumlich oder zeitlich ändern. (Die kinetische Energie und der Massenstrom haben zum Beispiel etwas mit der Geschwindigkeit zu tun, also mit einer zeitlichen Änderung.) Entsprechend hat das Gravitationsfeld auch einen Einfluss auf die räumliche und zeitliche Änderung und damit darauf, wie schnell oder in welchem Abstand Dinge sich ändern.
Wenn wir noch etwas genauer hingucken, dann können wir das auch an einer Größe festmachen, die in der Physik gern verwendet wird, nämlich der Wirkung. Die Wirkung ist eine Größe, die die kinetische und potentielle Energie eines Systems enthält. In der klassischen Physik gibt es das Prinzip der kleinsten Wirkung, das besagt, dass die Wirkung minimal wird. (Achtung, der Begriff “Wirkung” ist ziemlich unglücklich gewählt, das Prinzip besagt nicht, dass die Natur irgendwie besonders ökonomisch ist und alles möglichst effizient passiert oder so. Dass die Größe Wirkung heißt, ist im wesentlichen ein historischer Zufall.) Wen sich also zum Beispiel eine Welle mit einer bestimmten Wellenlänge oder Geschwindigkeit ausbreitet, dann tut sie das so, dass die Wirkung minimiert wird.
Haben wir ein Gravitationsfeld, dann geht dessen Einfluss direkt in die Wirkung ein. Meist interpretiert man das direkt über die Raum-Zeit-Krümmung und sagt, dass wir in der Wirkung (wo eben räumliche und zeitliche Änderungen drinstecken) berücksichtigen müssen, dass die Raumzeit gekrümmt ist. Wir können den entsprechenden Term aber genauso gut als Feld interpretieren und sagen, dass dieses Feld mit dem Rest unseres Systems wechselwirkt. Tatsächlich sieht das mathematisch ganz ähnlich aus zu der Wechselwirkung zwischen dem elektromagnetischen Feld und einem System, das elektrische Ladungen enthält. Insofern können wir den Einfluss der Gravitation also auch als Feld beschreiben.
Ist die Gravitation ein Feld wie jedes andere?
Im Feldbild scheint also an der Gravitation nicht viel besonderes zu sein. Ist die Gravitation also ein ganz gewöhnliches Feld genau wie das elektromagnetische Feld? Das könnte man jetzt in der Tat denken – und Einstein hat viele Jahre seines Lebens damit verbracht, andersherum zu versuchen, das elektromagnetische Feld mit einer Raumzeitkrümmung oder etwas ähnlichem in Verbindung zubringen. Warum geht das nicht? Was ist das Besondere am Gravitationsfeld?
Das elektromagnetische Feld wirkt nicht auf alle Materie – es gibt Materie, die geladen ist, und solche, die es nicht ist. Unterschiedliche Teilchen können unterschiedlich stark geladen sein, und reagieren dann auch unterschiedlich auf ein elektrisches Feld. Wenn ich zum Beispiel zwei Eisenatome habe und den einen eins, dem anderen zwei Elektronen klaue, so dass ich einfach oder zweifach ionisiertes Eisen bekomme, dann werden die beiden Eisenatome unterschiedlich stark im elektrischen Feld beschleunigt, denn das zweifach ionisierte Eisenatome erfährt die doppelte Kraft, hat aber dieselbe Masse.
Beim Gravitationsfeld ist das anders – dadurch das die schwere Masse gleich der trägen Masse ist, erfährt ein doppelt so schweres Atom zwar eine doppelt so große Kraft – man braucht aber auch eine doppelt so große Kraft, um es zu beschleunigen. Deswegen ist es sinnvoll auf der Erdoberfläche von einer Schwerebeschleunigung zu reden; es ist aber nicht besonders sinnvoll, eine Elektrobeschleunigung zu definieren, denn die ist für alle Ladungen unterschiedlich.
Am deutlichsten sehen wir den Effekt, wenn wir uns die fundamentale Theorie der Materie angucken, die Quantenfeldtheorie. (Falls ihr diesen Blog noch nicht so lange lest, klickt rechts bei den Artikelserien, da gibt es eine sehr lange Serie dazu. Die zu lesen ist aber nicht notwendig, um das Folgende zu verstehen.) In der Feldtheorie beschreiben wir die Materie durch Größen, die an jedem Punkt des Raums definiert sind (sehr stark vereinfacht kann man sich diese Größen als so etwas wie die Materiedichte vorstellen). Die Energie eines Materiefelds hängt davon ab, wie stark es sich räumlich und zeitlich ändert. Beschreibt das Feld Objekte mit Masse (also zum Beispiel Elektronen, aber keine Photonen), dann hängt die Energie auch direkt vom Wert des Felds selbst ab. (Anmerkung: Bei den Photonen ist es komplizierter – zwar ist die Energiedichte proportional zum Quadrat der Feldstärke, die Größe die in die fundamentalen Gleichungen eingeht, ist aber nicht das Feld selbst, sondern das Potential. Spielt aber für das Verständnis hier keine Rolle, ich schreibe es nur hin, damit sich niemand beschweren kann, dass hier Blödsinn steht.)
Ein schönes Beispiel für ein Feld (auch wenn die Größe des Feldes da nichts mit einer Dichte zu tun hat) ist ein gespanntes Gummituch (das habe ich auch ausführlich in der QFT-Serie verwendet, hier gibt es nur eine Kurzfassung). Um Energie in ein Gummituch zu bekommen, könnt ihr es auslenken. Damit sich das Tuch dehnt, müssen benachbarte Punkte unterschiedlich stark ausgelenkt sein – wenn ihr alle Punkte um den gleichen Betrag verschiebt, dehnt sich ja nichts, genauso wie in einem Gummiband nichts aufregendes passiert, wenn ihr es als Ganzes durch die Gegend schiebt. Stellt euch vor, an einem Punkt ist das Gummituch um einen Millimeter nach oben aus seiner Ruhelage verschoben, einen Millimeter weiter um drei Millimeter. Der Unterschied der Auslenkung beträgt dann zwei Millimeter (Auslenkung) pro Millimeter (Abstand).
Ich schreibe das mal als Gleichung für den Unterschied in der Auslenkung, den man Dehnung nennt (wenn ihr Gleichungen nicht mögt, könnt ihr sie auch querlesen oder überspringen, sie sind aber wirklich recht einfach):
Zu dieser Dehnung gehört eine Energie (die proportional zum Quadrat der Dehnung sein sollte, wenn ich mich nicht irre). Und jetzt stellt euch vor, ihr habt ein Schwerefeld. Dieses Feld wechselwirkt jetzt mit der im Tuch gespeicherten Energie – in die entsprechenden Gleichungen (für die Wirkung) geht der Wert des Feldes als Faktor ein. (Ich schaue hier nur darauf, wie das Feld das Tuch beeinflusst; natürlich erzeugt das Tuch seinerseits auch ein Schwerefeld, aber ich nehme einfach mal an, dass das deutlich schwächer ist als das äußere Feld.) Wir haben jetzt in den Gleichungen einen Term, der so aussieht (bis auf unwichtige Konstanten wie den Elastizitätsmodul):
Dabei habe ich einfach nur die Definition der Dehnung von oben eingesetzt. 1+Schwerefeld steht hier deshalb, weil ohne Schwerefeld die Energie ja trotzdem da ist, sie wird durch das Schwerefeld nur beeinflusst.
Und jetzt kommt der Trick: Wir können den Term (1+Schwerefeld) nach den Regeln der Bruchrechnung unter den Bruchstrich ziehen; wegen des Quadrats bekommen wir dann eine Wurzel an den Term, was aber fürs Prinzip ziemlich egal ist. (Expertinnenhinweis: Wer sich auskennt, erkennt aber, dass das natürlich damit zusammenhängt, dass die Metrik als Faktor in der Gleichung für ds² auftaucht.)
Egal ob ihr die Rechnung jetzt nachvollzogen habt oder nicht – entscheidend ist nur eins: Im letzten Ausdruck steht der Abstand geteilt durch einen Term, in den das Schwerefeld eingeht.
Ich kann die Gleichung hier also in zwei Weisen interpretieren – entweder als eine Gleichung für die Wechselwirkung von Gummituch und Schwerefeld, oder aber als eine Gleichung für das Gummituch, bei der sich aber der Abstand zwischen benachbarten Punkten von Ort zu Ort ändert, wobei diese Änderung gerade durch das “Schwerefeld” bestimmt ist. Und diese zweite Interpretation ist natürlich genau die, die zum Bild der Raumkrümmung führt – in dem Bild gibt es dann kein Schwerefeld mehr, dafür ändern sich eben Abstände auf seltsame Art von Ort zu Ort.
Diese zweite Interpretation funktioniert aber nur deswegen, weil der Einfluss auf den Abstand für alle Felder, die es gibt exakt derselbe ist. Auch bei der elektromagnetischen Wechselwirkung geht das Feld (genauer gesagt das Potential) in die entsprechenden Energieterme ein, dort steckt aber in der Gleichung noch die elektrische Ladung drin – je nachdem, wie groß die Ladung ist, ist der Effekt also unterschiedlich stark und ungeladene Teilchen wie Neutrinos merken gar nichts vom elektrischen Feld. Entsprechend kann man hier nicht einfach uminterpretieren und die Gleichungen als Gleichungen für eine gekrümmte Raumzeit auffassen (obwohl es genau das war, was Einstein lange versucht hat).
 In den entsprechenden Gleichungen kann man das übrigens direkt sehen: In den Gleichungen der Elektrodynamik taucht das Feld oder das Potential, wenn es um die Kopplung an Materie geht, immer zusammen mit der Ladung auf, beispielsweise in der Form
In den entsprechenden Gleichungen kann man das übrigens direkt sehen: In den Gleichungen der Elektrodynamik taucht das Feld oder das Potential, wenn es um die Kopplung an Materie geht, immer zusammen mit der Ladung auf, beispielsweise in der Form
Bei den Gleichungen für die Wechselwirkung eines Schwerefelds mit einem anderen Feld dagegen haben wir keinen zusätzlichen Ladungsterm an den Ableitungen (Formel aus den Feynman Lectures on Gravitation, Gl. 4.2.8):
Daran sieht man schon formelmäßig, dass das Schwerefeld (der Tensor h als Abweichung von der Minkowski-Metrik) nicht von irgendeiner besonderen Eigenschaft des Feldes wie etwa der Ladung abhängt. Die Masse geht ein, allerdings nicht in den Ableitungstermen.  Das muss auch so sein, denn die Masse hat in der Feldtheorie einen Einfluss auf die Feldoszillationen – wenn wir die (mit dem Maßstab) ändern wollen, dann muss die Masse auch beeinflusst werden.
Das muss auch so sein, denn die Masse hat in der Feldtheorie einen Einfluss auf die Feldoszillationen – wenn wir die (mit dem Maßstab) ändern wollen, dann muss die Masse auch beeinflusst werden.
Für die Zeit funktioniert die Überlegung übrigens ganz genauso – die Bewegungsenergie des Gummituchs hängt davon ab, wie stark sich die Auslenkung mit der Zeit ändert (denn wenn es auf- und abschwingt, bekomme ich ja eine Bewegung). In der entsprechenden Gleichung teilt man also durch den zeitlichen Abstand (weil man ja bei einer Geschwindigkeit die zurückgelegte Strecke durch die Zeit teilt), und auch hier kann man die Gleichung wie oben angegeben umschreiben.
Das Gravitationsfeld ist also insofern besonders, als es direkt mit der Energie wechselwirkt. Das führt dazu (weil letztlich in allen denkbaren Feldern die Energie von der räumlichen und zeitlichen Änderung des Felds abhängen muss), dass das Feld auf alle anderen Felder gleich wirkt. Und nur deswegen können wir die Stärke des Feldes in den Gleichungen auch genauso gut in die jeweiligen Größen einbauen, die den Abstand (und damit letztlich den Ort und die Zeit) kennzeichnen.
Puh. Ich weiß nicht, wie lange ich mich schon mit der Frage herumärgere, wie man sich zumindest halbwegs anschaulich zusammenreimen kann, dass gerade die Gravitation diese zwei Interpretationen erlaubt. Zumindest für mich machen diese Überlegungen die Sache einigermaßen nachvollziehbar: Die Gravitation muss an den Energiegehalt koppeln, die entsprechenden Terme in den Gleichungen enthalten immer räumliche und zeitliche Änderungen, also kann ich den Ausdruck, der das Gravitationsfeld enthält, auch den jeweiligen Abstandsvariablen zuschlagen – was dazu führt, dass sich räumliche und zeitliche Abstände scheinbar ändern. Ob Euch die Erklärung auch weiterhilft, weiß ich nicht, aber ich habe gerade das Gefühl, endlich etwas begriffen zu haben, was als Frage seit Jahren in meinem Kopf herumspukt. Hinterlasst gern jede Menge nörgelnde Kommentare, wenn die Erklärung hier nicht klar ist, weil sie nur auf meine persönliche Intuition passt.
Zum Abschluss mal wieder eine Warnung: Das, was ich hier geschrieben habe, steht so meines Wissens in keinem Buch – jedenfalls in keinem, das ich kenne. Ich bin mir zu 99% sicher, dass es stimmt (von kleinen Unsauberkeiten mal abgesehen), aber ich übernehme keine Garantie. Warum das in keinem Buch steht, ist ne ganz andere Frage, sooo selbstverständlich finde ich es zumindest nicht…






Kommentare (128)