Mit anderen Worten: Zu jeder Amplitude gibt es eine zugehörige Wahrscheinlichkeit (oder eine Wahrscheinlichkeitsdichte, wenn ihr Mathematikerin seid und es genau nehmt), dass ihr (wenn ihr das elektrische Feld messen würdet) gerade diesen Wert der Amplitude bekommt. Diese Wahrscheinlichkeit hängt nicht von der Zeit ab – deswegen habe ich dreimal dasselbe Bild gezeichnet. Ein solcher Zustand ist also stationär und kann eine genau definierte Energie haben.
So etwa (allerdings nicht quantitativ korrekt, ich war etwas schlampig) sieht die Wahrscheinlichkeit für die unterschiedlichen Amplituden aus:
Die Wahrscheinlichkeit, als Amplitude genau den Wert Null zu messen, ist also gleich Null, bei den positiven und negativen Werten gibt es jeweils ein Maximum. (Wenn ihr das Bild um 90° dreht, dann bekommt ihr die Intensität der Kurven aus dem Bild oben.)
Hier haben wir jetzt also einen Zustand, den man als “Photon” bezeichnen könnte. Es ist allerdings ein ausgedehnter Zustand – er ist im gesamten zur Verfügung stehenden Raum zwischen den Spiegeln nicht Null. So ganz passt das zu unserer Vorstellung eines “Teilchens” noch nicht.
Würden wir aber ein Atom zwischen die Spiegel setzen, das eine Energie der Größe E=hν aufnehmen kann, dann könnte dieses Atom durch unser em-Quantenfeld in den energetisch höheren Zustand angeregt werden. Wir könnten dann sagen “Das Atom hat ein Photon absorbiert”. Umgekehrt könnte das angeregte Atom wider in den Grundzustand zurückfallen und dabei wieder ein em-Quantenfeld mit Energie E=hν wie im Bild erzeugen. In diesem Sinn können wir also durchaus von einem Teilchen sprechen. Für die Teilcheninterpretation spricht auch, dass wir dem Feld nicht bloß einen Teil seiner Energie entziehen können – wir können entweder die ganze Energie hν absorbieren oder nicht, aber nicht bloß einen Teil, weil es dazu keine passenden Zustände gibt. Das ist ja genau die Bedeutung der Aussage “Die Energie ist quantisiert” – sie kann (bei einer Wellenlänge) nur in Paketen bestimmter Größe absorbiert oder emittiert werden. (In der klassischen Physik dagegen kann die Amplitude einer em-Welle beliebige Werte annehmen.)
2. Höhere Anregungen
Bisher hatten wir ein Photon zwischen unseren Spiegeln – mit einer Energie von hν. (Expertinnenhinweis: ich spare mir hier die Diskussion der Nullpunktsenergie – die findet ihr aber z.B. in der QFT-Serie im Artikel “Wir verstehen Nichts”.) Aus dem Alltag wissen wir, das Licht aber auch deutlich größere Energien mit sich herumtragen kann (die Energie eines einzelnen Photons des sichtbaren Lichts ist ziemlich winzig).
In der klassischen Physik ist das einfach – eine höhere Energie entspricht einer größeren Amplitude. Da die Amplitude quadratisch eingeht, brauche ich für eine doppelt so hohe Energie also eine Amplitude, die um einen Faktor √ 2 größer ist. Es spricht aber nichts gegen beliebige Werte der Amplitude.
In der Quantenbeschreibung unserer em-Welle sieht das ganze deutlich anders aus. Wen nwir die doppelte Energie in unserer Welle haben wollen (also E=2hν), dann haben wir auch wieder einen Überlagerungszustand. Der sieht diesmal etwa so aus:
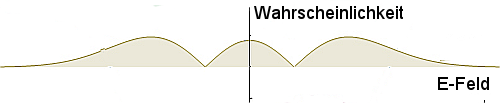
Wir haben diesmal drei Werte der Amplitude, bei denen die Wahrscheinlichkeit ein Maximum hat – einen bei Null und zwei bei positiven und negativen Werten:
Wenn wir jetzt wieder ein Atom zwischen unsere Spiegel packen, dass Energien von hν absorbieren kann, dann kann es dem Zustand diese Energie entziehen – das Atom gerät dann in einen angeregten Zustand, der Zustand des em-Feldes ändert sich dann und wird zum Ein-Photon-Zustand von oben.
Genau wie eben können wir – weil wir dem System die Energie in zwei Quanten der Größe hν entziehen können – jetzt von einem Zustand mit zwei Photonen sprechen.
Zustände mit drei, vier oder noch mehr Photonen gehen genau so – dort hat man ein immer komplizierteres Muster aus Maxima und Minima der jeweiligen Amplituden.








Kommentare (136)