Photonen sind – das haben die meisten vermutlich schon einmal gehört – die Teilchen, aus denen Licht besteht. Klingt auf den ersten Blick einigermaßen einfach, oder? Fragt man aber acht Physikerinnen, was ein Photon ist, so erhält man etwa zehn Antworten (so geschehen im Jahr 2003 in einer Ausgabe von Optics&Photonics News, Quelle s.u.). Es gibt sogar eine Konferenz-Serie zum Thema: “The Nature of Light: What are photons?”
Also – was ist denn nun ein Photon?
Warnung: Die meisten der Dinge, die ich hier schreibe, stehen so meines Wissens in keinem Buch. Ich bin mir ziemlich sicher, dass alles stimmt, aber ich übernehme wie üblich keine Garantie.
W.E. Lamb, eine berühmte Physikerin*, hat einen Artikel mit dem Titel “Anti-Photon” geschrieben, in dem es heißt:
“It should be apparent from the title of this article that the author does not like the use of the word “photon”, which dates from 1926. In his view, there is no such thing as a photon. Only a comedy of errors and historical accidents led to its popularity among physicists and optical scientists.”
[Aus dem Titel des Artikels sollte offensichtlich sein, dass die Autorin die Verwendung des Wortes “Photon”, das im Jahr 1926 erfunden wurde, nicht mag. In ihrer Sicht gibt es so etwas wie ein Photon nicht. Nur eine Komödie der Irrungen und historische Zufälle haben zu seiner Popularität unter Physikerinnen und optischen Wissenschaftlerinnen geführt.]
*Ja, ich verwende nach wie vor ausschließlich weibliche Formen. Wer sich darüber aufregen will, kann das hier tun; Kommentare bei diesem Artikel hier werde ich schlicht löschen. Und nein, das ist keine Zensur.
Fragen wir erst Mal Wikipedia, für Physik-Fragestellungen meist keine schlechte erste Adresse. Dort lesen wir:
Das Photon (von griechisch φῶς phōs, Genitiv φωτός phōtos ‚Licht‘) ist das Elementarteilchen (Quant) des elektromagnetischen Feldes. Anschaulich gesprochen sind Photonen das, woraus elektromagnetische Strahlung besteht, daher wird gelegentlich auch die Bezeichnung Lichtquant oder Lichtteilchen verwendet.
Das Photon ist also “Das Elementarteilchen des em-Feldes”. Man kann sich laut dieser Erklärung also vorstellen, dass Licht aus Photonen besteht, genauso wie Materie aus Atomen (oder wenn man genauer hinguckt, Elektronen und Quarks) besteht. Klingt erst mal unproblematisch, oder?
Tatsächlich gibt es aber einige Unterschiede zwischen Elektronen (die nehme ich jetzt mal als Beispiel) und Photonen – deswegen werdet ihr vermutlich auch keine Konferenzserie mit dem Titel “What are Electrons?” finden.
Zunächst einmal kann man Elektronen problemlos auf einen sehr kleinen Raum einsperren – ein Elektron kann beispielsweise in einem Quantenpunkt gefangen sein (das ist ein winziges Stück Metall), aus dem es nicht entkommen kann, und dank seiner elektrischen Ladung können wir auch leicht messen, ob es da ist (oder ob es vielleicht sogar zwei oder drei Elektronen sind). Wir können auch die Bahn eines Elektrons verfolgen, beispielsweise in einem Detektor für Elementarteilchen wie einer Blasenkammer:
Quelle: CERN, Teachers Web
Hier seht ihr, wie ein einfliegendes (nicht sichtbares) “Photon” ein Elektron-Positron-Paar erzeugt, dessen Weg wir verfolgen können. (Die Wege sind gekrümmt, weil man ein Magnetfeld anlegt; geladene Teilchen werden im Magnetfeld abgelenkt.)
Elektronen können also lokalisiert werden – wir können herausfinden, wo sie sich gerade aufhalten. (Ja, es gibt, die Unschärferelation, die uns da gewisse Grenzen setzt, aber zu einem bestimmten Zeitpunkt kann man ein Elektron beliebig gut an einen Ort festnageln – die Unschärferelation sorgt dann allerdings dafür, dass wir nichts mehr über seine Geschwindigkeit wissen können, so dass im nächsten Moment vermutlich ganz woanders ist. Mehr über die Unschärferelation findet ihr z.B. in der Artikelserie zu Schrödingergleichung – klickt rechts bei den Artikelserien.)
Außerdem sind – wie schon erwähnt – Elektronen elektrisch geladen (deswegen heißen die ja so). Die elektrische Ladung hat zwei Eigenschaften: Zum einen ist sie quantisiert, sie kann also nicht beliebige Werte annehmen. Zum anderen ist sie eine Erhaltungsgröße, Ladungen entstehen also nicht einfach so. Ich kann zwar aus einem ungeladenen “Photon” ein Elektron erzeugen (so wie in dem Bild oben), aber nur, wenn ich gleichzeitig auch ein Teilchen mit einer positiven Ladung erzeuge.
Das führt dazu, dass – im Prinzip, von technischen Schwierigkeiten abgesehen – die Zahl der Elektronen in einem abgeschlossenen System immer eindeutig bestimmt ist (jedenfalls, solange wir keine Wechselwirkungen mit einbeziehen, wenn es die gibt, wird es komplizierter).
Alle diese Dinge gelten für Photonen nicht, oder nur sehr eingeschränkt – man kann sie nicht ohne weiteres lokalisieren, und man kann sie auch nicht immer ohne weiteres zählen. (Falls ihr einen Laserpointer habt – wenn ihr mit dem einen Lichtpuls erzeugt, dann ist die Zahl der Photonen darin unbestimmt, wie wir nachher noch sehen werden.)
Bevor wir uns gleich anschauen, wie Licht sich nun im einzelnen verhält (und was man alles unter einem “Photon” verstehen kann), erst mal eine kleine Erinnerung an eine der Grundregeln der Quantenmechanik (ausführlich habe ich das hier erklärt): Anders als in der klassischen Physik können quantenmechanische Systeme in einem sogenannten Überlagerungszustand sein. Man erklärt das gern am einfachen Beispiel einer Münze: Ein klassischer Taler, der auf dem Tisch liegt, zeigt entweder “Kopf” oder “Zahl”. Ein Quantentaler dagegen kann in einem Überlagerungszustand sein, sozusagen 30% Kopf und 70% Zahl. Schaut man hin (vornehm gesagt “macht man eine Messung”), was der Taler zeigt, dann bekommt man in 30% der Fälle Kopf zu sehen, in 70% der Fälle Zahl. Die Wahrscheinlichkeit gibt aber hier nicht bloß unsere Unkenntnis an, was der Taler tatsächlich gerade tut – er ist wirklich in einem solchen komplizierten Überlagerungszustand. (Nachweisen kann man das mit Hilfe der so genannten Verschränkung – die erkläre ich im dritten Teil der gerade verlinkten Artikelseire, oder auch recht kurz in diesem Artikel. ich habe hier auch arg vereinfacht, denn eigentlich muss man Wahrscheinlichkeitsamplituden angucken, die komplexe Zahlen sind; für ein prinzipielles Verständnis ist das aber nicht so wichtig.)
Wie wir gleich sehen werden, wird diese Überlagerung ziemlich wichtig, wenn es um die Frage geht, was ein Photon ist.
Die Energie eines Photons
Nach dem Wiki-Artikel ist ein Photon ja ein “Quant” der em-Strahlung. “Quant” bedeutet hier, dass die Energie eines Photons nicht beliebige Werte annehmen kann, sondern nur ganz bestimmte Werte. Für diese Energie gilt, dass sie gleich der Frequenz multipliziert mit einer Zahl, dem Planckschen Wirkungsquantum, ist. (Die Frequenz (mit ν abgekürzt) sagt etwas darüber aus, wie schnell eine Welle oszilliert – das sehen wir gleich noch genauer.) In Formeln schreibt man E=hν. Das h steht für’s Plancksche Wirkungsquantum, das einfach eine physikalische Konstante ist. Damit wir etwas als “Photon” bezeichnen können, sollte seine Energie also irgendwie durch diese Formel beschreibbar sein. Ob das später immer so bleibt, werden wir noch sehen, aber als Ausgangspunkt ist es erst mal ziemlich sinnvoll.
So, und jetzt gucken wir uns zunehmend komplizierte Situationen an, in denen man von “Photonen” sprechen kann. (Eifrige Leserinnen des Blogs kennen einen guten Teil der Argumente übrigens schon von hier.)
1.Die stehende Welle
Photonen – wenn es sie denn gibt – sind ja laut Wikipedia die Quanten des elektromagnetischen Feldes. Schauen wir erst mal auf die klassische Physik: Da kann ein em-Feld im Vakuum existieren, nämlich in Form einer elektromagnetischen Welle. Als einfachstes Beispiel dafür können wir uns zwei Spiegel aus Metall vorstellen – die haben die Eigenschaft, dass auf ihrer Oberfläche ein elektrisches Feld nur senkrecht stehen könnte, ansonsten würden sich Ladungen im Metall verschieben, weil elektrische Ladungen ja auf elektrische Felder reagieren. Zwischen zwei solchen Spiegeln kann sich eine stehende Welle ausbilden – ganz ähnlich wie bei einer Saite, die man zupft, eine stehende Welle entstehen kann.
Wir betrachten erst einmal den einfachsten Fall und machen die Welle so groß wie es eben geht, so dass genau ein “Schwingungsbauch” zwischen die Spiegel passt. (Der Einfachheit halber betrachte ich erst einmal auch nur Fälle, wo das elektrische Feld immer genau nach “oben/unten” im Bild zeigt). Die Welle schwingt dann hin und her – oder anders gesagt, das elektrische Feld an jedem Punkt zwischen den Spiegel oszilliert:
In grün ist hier die Stärke des Feldes zwischen den Spiegeln eingezeichnet, krümmt sich die Linie nach oben, zeigt das Feld ebenfalls nach oben (ich habe an einer Stelle einen Pfeil eingezeichnet, um das zu veranschaulichen). Würden wir eine elektrische Ladung zwischen die Spiegel platzieren, dann würde sie durch das schwingende elektrische Feld ebenfalls zu Schwingungen angeregt.
Tatsächlich habe ich das ganze hier vereinfacht – zusätzlich zum elektrischen Feld muss es auch ein Magnetfeld geben, das ebenfalls oszilliert, die beiden hängen zusammen. Ich habe mir das hier gespart, weil es sonst gleich sehr unübersichtlich wird und weil das Magnetfeld letztlich immer so ziemlich dasselbe tut wie das E-Feld. Wenn ihr genau wissen wollt, wie die beiden Felder zusammenhängen, könnt ihr rechts bei den Artikelserien klicken, da gibt es eine lange Serie zur Maxwellgleichung der Elektrodynamik, und im dritten Teil wird eine Welle zusammengebastelt.
Schnell noch ein paar Begriffe, die brauchen wir später vermutlich des öfteren: Die Frequenz einer em-Welle ist der Kehrwert der Zeit, die die Welle braucht, um wieder im Anfangszustand zu sein – wenn ich vom Bild links oben zum Bild rechts unten gehe, dann hat sich die Welle genau auf den Kopf gestellt. Wenn sie dafür 5 Sekunden braucht, dann braucht sie insgesamt 10 Sekunden, um wieder den Anfangszustand zu erreichen (wir laufen sozusagen das Bild rückwärts), die Frequenz, abgekürzt mit dem griechischen Buchstaben ν (“Ny”), wäre dann 0,1 Hertz (mit “t”, nach Heinrich Hertz benannt). Die zweite wichtige Größe ist die Wellenlänge – die ist bei einer Welle meist definiert als der Abstand von einem Schwingungsmaximum zum nächsten. Da wir hier nur einen Schwingungsbauch haben, ist diese Definition nicht so praktisch – alternativ kann man aber die Wellenlänge definieren als den doppelten Abstand zwischen zwei Nulldurchgängen. Die Wellenlänge unserer Welle ist also doppelt so groß wie der Abstand zwischen den Spiegeln. Schließlich gibt es noch die Amplitude – das ist der Wert des Feldes im Maximum.
Wie ändert sich jetzt das Bild, wenn wir von der klassischen Physik zur Quantenbeschreibung übergehen?
Ich denke, wenn man 100 Physikerinnen fragen würde, würden 80 davon in etwa folgendes sagen (hätte ich vor einigen Jahren vermutlich auch getan):
Die Energie eines elektromagnetischen Feldes ist proportional zum Quadrat der elektrischen Feldstärke. (Das weiß man aus der klassischen Physik.) Wenn diese Energie nach der Einstein-Beziehung E=hν quantisiert sein soll, dann ist das elektrische Feld entsprechend so groß, dass die Energie des Photons genau diesen Wert hat. Das Maximum des elektrischen Feldes kann also nicht beliebige Werte annehmen, sondern nur einen ganz bestimmten Wert.
Das sieht auf den ersten Blick jedenfalls sehr plausibel aus, und es passt zu E=hν. Leider ist es falsch.
Dass es falsch ist, kann man sich – mit etwas Physik-Hintergrundwissen – sofort überlegen: In der Quantenmechanik gilt (leicht vereinfacht) die Aussage, dass bei einem Zustand mit genau definierter Energie alle beobachtbaren Größen zeitunabhängig sind. Da man elektrische Felder ja messen kann, ist ein Zustand, bei dem sich das Feld zeitlich so ändert wie im Bild oben, niemals ein Zustand mit einer genau definierten Energie, ein solcher Zustand kann also nicht die Gleichung E=hν erfüllen.
Wenn ein Photon also ein Quant des em-Feldes mit Energie hν ist, dann ist das, was wir gerade beschrieben haben, jedenfalls kein Photon, denn ein solcher Zustand kann keine genau definierte Energie haben.
Damit wir einen Zustand mit genau definierter Energie bekommen, brauchen wir also einen Zustand, der sich zeitlich nicht ändert. Sieht der Zustand also einfach so aus wie oben im ersten Teilbild, so dass nichts mehr schwingt, sondern das elektrische Feld einfach zeitlich konstant ist? Nein – so einen Zustand kann es auch nicht geben, der ist nicht mit den Gleichungen der Elektrodynamik vereinbar.
Um einen echten Ein-Photon-Zustand zu bekommen, müssen wir eine quantenmechanische Überlagerung basteln. Wir überlagern sozusagen einfach die unterschiedlichen Wellen, die wir oben hatten, etwa so:
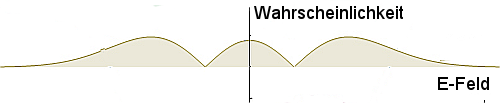
Das Bild muss ich erst mal ausführlich erklären. Nach wie vor kennzeichnet grün die Stärke des elektrischen Feldes. Zusätzlich habe ich jetzt aber die einzelnen Wellen unterschiedlich kräftig gezeichnet – je kräftiger eine Welle ist, desto größer ist ihre Wahrscheinlichkeit (denkt wieder an den Quantentaler). Es gibt also jeweils einen Wert des elektrischen Feldes (der Amplitude), der am wahrscheinlichsten ist, aber auch größere und kleinere Werte tragen bei. Natürlich sind es in Wahrheit nicht bloß die acht eingezeichneten Wellen, die man berücksichtigen muss, sondern alle denkbaren Werte tragen bei (es ist mir aber nicht gelungen – oder ich war zu faul…- , das vernünftig zu zeichnen).
Mit anderen Worten: Zu jeder Amplitude gibt es eine zugehörige Wahrscheinlichkeit (oder eine Wahrscheinlichkeitsdichte, wenn ihr Mathematikerin seid und es genau nehmt), dass ihr (wenn ihr das elektrische Feld messen würdet) gerade diesen Wert der Amplitude bekommt. Diese Wahrscheinlichkeit hängt nicht von der Zeit ab – deswegen habe ich dreimal dasselbe Bild gezeichnet. Ein solcher Zustand ist also stationär und kann eine genau definierte Energie haben.
So etwa (allerdings nicht quantitativ korrekt, ich war etwas schlampig) sieht die Wahrscheinlichkeit für die unterschiedlichen Amplituden aus:
Die Wahrscheinlichkeit, als Amplitude genau den Wert Null zu messen, ist also gleich Null, bei den positiven und negativen Werten gibt es jeweils ein Maximum. (Wenn ihr das Bild um 90° dreht, dann bekommt ihr die Intensität der Kurven aus dem Bild oben.)
Hier haben wir jetzt also einen Zustand, den man als “Photon” bezeichnen könnte. Es ist allerdings ein ausgedehnter Zustand – er ist im gesamten zur Verfügung stehenden Raum zwischen den Spiegeln nicht Null. So ganz passt das zu unserer Vorstellung eines “Teilchens” noch nicht.
Würden wir aber ein Atom zwischen die Spiegel setzen, das eine Energie der Größe E=hν aufnehmen kann, dann könnte dieses Atom durch unser em-Quantenfeld in den energetisch höheren Zustand angeregt werden. Wir könnten dann sagen “Das Atom hat ein Photon absorbiert”. Umgekehrt könnte das angeregte Atom wider in den Grundzustand zurückfallen und dabei wieder ein em-Quantenfeld mit Energie E=hν wie im Bild erzeugen. In diesem Sinn können wir also durchaus von einem Teilchen sprechen. Für die Teilcheninterpretation spricht auch, dass wir dem Feld nicht bloß einen Teil seiner Energie entziehen können – wir können entweder die ganze Energie hν absorbieren oder nicht, aber nicht bloß einen Teil, weil es dazu keine passenden Zustände gibt. Das ist ja genau die Bedeutung der Aussage “Die Energie ist quantisiert” – sie kann (bei einer Wellenlänge) nur in Paketen bestimmter Größe absorbiert oder emittiert werden. (In der klassischen Physik dagegen kann die Amplitude einer em-Welle beliebige Werte annehmen.)
2. Höhere Anregungen
Bisher hatten wir ein Photon zwischen unseren Spiegeln – mit einer Energie von hν. (Expertinnenhinweis: ich spare mir hier die Diskussion der Nullpunktsenergie – die findet ihr aber z.B. in der QFT-Serie im Artikel “Wir verstehen Nichts”.) Aus dem Alltag wissen wir, das Licht aber auch deutlich größere Energien mit sich herumtragen kann (die Energie eines einzelnen Photons des sichtbaren Lichts ist ziemlich winzig).
In der klassischen Physik ist das einfach – eine höhere Energie entspricht einer größeren Amplitude. Da die Amplitude quadratisch eingeht, brauche ich für eine doppelt so hohe Energie also eine Amplitude, die um einen Faktor √ 2 größer ist. Es spricht aber nichts gegen beliebige Werte der Amplitude.
In der Quantenbeschreibung unserer em-Welle sieht das ganze deutlich anders aus. Wen nwir die doppelte Energie in unserer Welle haben wollen (also E=2hν), dann haben wir auch wieder einen Überlagerungszustand. Der sieht diesmal etwa so aus:
Wir haben diesmal drei Werte der Amplitude, bei denen die Wahrscheinlichkeit ein Maximum hat – einen bei Null und zwei bei positiven und negativen Werten:
Wenn wir jetzt wieder ein Atom zwischen unsere Spiegel packen, dass Energien von hν absorbieren kann, dann kann es dem Zustand diese Energie entziehen – das Atom gerät dann in einen angeregten Zustand, der Zustand des em-Feldes ändert sich dann und wird zum Ein-Photon-Zustand von oben.
Genau wie eben können wir – weil wir dem System die Energie in zwei Quanten der Größe hν entziehen können – jetzt von einem Zustand mit zwei Photonen sprechen.
Zustände mit drei, vier oder noch mehr Photonen gehen genau so – dort hat man ein immer komplizierteres Muster aus Maxima und Minima der jeweiligen Amplituden.
3. Andere Wellenlängen
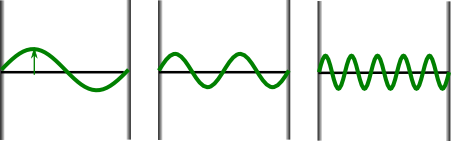
Ähnlich wie bei einer Saite, die man zum Schwingen bringt, kann man auch zwischen zwei Spiegeln Schwingungen mit “Obertönen” anregen. In der klassischen Physik sehen die Wellen dann beispielsweise so aus:
Links haben wir eine Welle, bei der die Wellenlänge gleich dem Abstand der Spiegel ist, in der Mitte eine mit Wellenlänge gleich halbem und rechts mit Wellenlänge gleich einem Fünftel Spiegelabstand. Diese Wellen oszillieren in der klassischen Physik genau so hin und her wie die Welle oben, und auch das Quantenbild dieser Wellen sieht letztlich genauso aus wie oben, also beispielsweise so (für einen Ein-Photon-Zustand):
Die Energie zu diesen Wellen ist größer als die Energie der Welle oben – da Frequenz und Wellenlänge umgekehrt proportional sind, habe ich hier wegen der kleineren Wellenlänge größere Frequenzen.
Wenn wir – damit wir nicht durcheinanderkommen, weil wir jetzt verschiedene Frequenzen haben – die Frequenz der Welle oben mit nur einem Schwingungsbauch mit ν0 bezeichnen, dann hat die Welle links (mit der halben Wellenlänge) die Energie E=2hν0. Ihr seht also, dass man eine Energie von 2hν0 auf zwei unterschiedliche Weisen bekommen kann: Entweder als Zwei-Photonen-Zustand zur Welle mit einem Schwingungsbauch, oder als Ein-Photonen-Zustand zur Welle mit zwei Schwingungsbäuchen.
Hinweis: Ja, dieser Artikel ist ziemlich lang. Ich habe überlegt, ihn in mehrere Teile zu zerhacken, habe mich aber dagegen entschlossen, damit man am Ende alles an einer Stelle zusammengefasst hat. Falls euch schon der Kopf schwirrt, macht im Zweifel ne Pause und lest später wieder weiter…
4. Überlagerungen
Wenn ihr die Überschrift dieses Abschnitts lest, denkt ihr vielleicht “Wieso Überlagerungen? Wir hatten doch schon Überlagerungen?” Aber wir können die bisherigen Zustände – so kompliziert sie auch schon waren – auch noch überlagern. Beispielsweise so:
Hier haben wir jetzt eine 70%ige Wahrscheinlichkeit, das Feld im linken Zustand vorzufinden – wenn wir beispielsweise die Energie messen, dann haben wir eine Wahrscheinlichkeit von 70% für den Wert E=hν0, und mit 30% Wahrscheinlichkeit messen wir E=4hν0.Der Zustand hier hat also keine eindeutige Energie (er ist deswegen auch nicht stationär, das gucken wir uns gleich an).
Messen wir die Amplitude und Wellenlänge (wie auch immer wir das anstellen), so bekommen wir eine Welle, die wir mit einer Wahrscheinlichkeit von x% messen, wenn wir nur den linken Zustand haben, jetzt mit einer Wahrscheinlichkeit von 0,7 x%.
Fragen wir uns dagegen, wie viele Photonen wir haben, so ist die Antwort klar: Eins. Denn wir haben einen Überlagerungszustand aus zwei Zuständen, in denen die Zahl der Photonen jeweils gleich Eins ist – wenn wir also die Photonenzahl messen (man könnte beispielsweise einen Halbleiterdetektor verwenden, denke ich (dessen Bandlücke müsste kleiner sein als hν0)), dann messen wir immer 1 Photon, nicht zwei oder 17 oder null. Insofern ist dieser Zustand hier ein Ein-Photonen-Zustand. Ob man ihn tatsächlich als “Ein Photon” bezeichnen möchte, ist schon schwieriger zu beantworten, denn wir haben ja keine klar definierte Energie mehr.
5. Wellenpakete
Wenn man sich ein Photon vorstellt, dann denkt man typischerweise an ein Teilchen, das irgendwo losfliegt und dann irgendwann woanders ankommt. Unsere photonen-Zustände hier haben diese Eigenschaft nicht – sie sind zwischen den Spiegel ausgebreitet. Irgendwie muss es aber doch möglich sein, Photonen wie einen Lichtpuls auszusenden, oder?
Ja, ist es. Dazu brauchen wir allerdings auch wieder Überlagerungszustände. (Im einzelnen habe ich den Trick, den wir hier brauchen, in der QFT-Serie erklärt.) Überlagerungen von Wellen kann man schon in der klassischen Physik bekommen. Dort können wir uns einen Lichtpuls ja etwa so vorstellen:
Wir haben ein elektrisches Feld (das Magnetfeld zeichne ich wie immer nicht mit), das nach außen verschwindet, dann ein Maximum hat und wieder abfällt. Dieses Paket bewegt sich jetzt als ganzes mit Lichtgeschwindigkeit vorwärts.
Mathematisch kann man so ein Paket als Summe aus lauter einzelnen Wellen schreiben (genauer gesagt, als Integral) – man muss Wellen mit unterschiedlichen Wellenlängen addieren, um so ein Paket herauszubekommen. (Relativ kurz habe ich das auch hier schon mal erklärt.) Wenn ihr euch das Wellenpaket genau anseht, seht ihr, dass es nicht ganz einfach ist, die Wellenlänge genau zu messen – wenn ihr den Abstand zwischen zwei Wellenbergen messt, stellt ihr fest, dass der nicht immer gleich ist, was daran liegt, dass wir unsere Welle zu den Rändern hin ja immer weiter abflachen. Das Wellenpaket hat also keine eindeutige Wellenlänge (und auch keine eindeutige Frequenz), sondern unterschiedliche Wellenlängen tragen zum Paket bei.
Wenn wir jetzt den Übergang zur Quanten-Beschreibung machen, müssen wir entsprechend die einzelnen Quantenzustände von oben genau so überlagern. Das Ergebnis für unser Wellenpaket sieht dann etwa so aus:
Ein solches Wellenpaket hat wie gesagt keine genau definierte Wellenlänge und Frequenz, wenn aber hinreichend viele Wellenberge im Paket enthalten sind, dann tragen nur Wellen bei, deren Wellenlänge in etwa der “Grundwellenlänge” entspricht. So ein paket hat also zumindest näherungsweise eine Wellenlänge und eine Frequenz, allerdings mit einer gewissen Unschärfe.
Entsprechend ist auch die Energie des Pakets unscharf – sie ist etwa hν, aber eben mit einer gewissen Unsicherheit. (Das muss ja auch so sein, denn Zustände mit genau definierter Energie sind wie gesagt ja stationär, ein solcher Zustand könnte nicht als Wellenpaket von Ort zu Ort laufen.)
Wenn ihr euch als Photon also etwas vorstellen wollt, das an einem Ort ausgesandt wird und dann an einem anderen Ort ankommt, dann ist so ein Wellenpaket eine gute Anschauung dafür. Allerdings erkauft ihr euch die Paketnatur damit, dass die Energie nicht mehr ganz genau festgelegt ist, sie ist nicht exakt hν, sondern eben nur näherungsweise. Ein Photon, das mit genau der Energie hν von einem Ort zum andern läuft, lässt sich nicht realisieren.
Auch beim Wellenpaket können wir dasselbe Spiel mit höheren Anregungen spielen – wir können also lauter zwei-Photonen-Zustände überlagern und bekommen dann ein Wellenpaket, das die Ausbreitung von zwei Photonen beschreibt.
6. Kohärente Zustände
Alle Zustände, die wir bisher angeguckt haben, hatten eine besondere Eigenschaft: Die Wahrscheinlichkeit war für positive und negative Amplituden jeweils gleich, das Bild war immer symmetrisch um die horizontale Null-Linie. Das bedeutet, dass das elektrische Feld im Mittel immer gleich Null ist. (Vornehm ausgedrückt: Der Erwartungswert des Feldes verschwindet.) Ist es denn überhaupt möglich, eine Quantenversion unserer klassischen Welle zu bekommen, bei der das Feld (bzw. sein Mittelwert) zwischen positiven und negativen Werten oszilliert?
Ja, das geht. Solche Zustände nennt man kohärente Zustände, und man kann sie konstruieren. Laserlicht beispielsweise ist in einem solchen kohärenten Zustand. Mit kohärenten Zuständen ist es tatsächlich möglich, ein oszillierendes elektrisches Feld zu haben, so wie in unserem klassischen Bild ganz oben.
Um so einen Zustand zu bekommen, braucht man wieder einmal eine Überlagerung. Jetzt müssen wir allerdings Zustände mit unterschiedlicher Anzahl von Photonen in geeigneter Weise überlagern. Wir brauchen also so eine Überlagerung (hier war zuerst ein falsches Bild, danke an Alex für den Hinweis):
Dabei geht die Summe weiter zu immer höheren Zuständen, die aber immer weniger beitragen. Wie groß die Beiträge der einzelnen Zustände sind, hängt davon ab, wie groß ihr die Amplitude haben wollt (ich habe das hier vorsichtshalber nicht ausgerechnet, dabei wird dann auch wichtig, dass man als Vorfaktoren Wahrscheinlichkeitsamplituden hat, die auch negative Werte annehmen können.)
Da die einzelnen Zustände unterschiedlich große Energien haben, ist damit die Energie des kohärenten Zustands nicht genau definiert – wenn ihr die Energie messt, dann zerstört ihr den Zustand. Das kann man experimentell tatsächlich umsetzen und ganz vorsichtig die Zahl der Photonen in einem kohärenten Zustand messen; je mehr Informationen man über die Photonenzahl bekommt, desto stärker wird der kohärente Zustand gestört. Weil das nicht nur cool, sondern auch knifflig ist, gab’s 2012 dafür den Nobelpreis.
7. Virtuelle Photonen
Manchmal fällt der Begriff “Photon” auch im Zusammenhang mit den sogenannten “virtuellen Photonen”. Aber dieser Artikel ist zum einen schon seeehr lang, zum anderen habe ich darüber schon anderweitig gebloggt – wenn ihr mehr Bedarf am Thema habt, schreibt einen Kommentar, vielleicht erklär ich’s dann nochmal anders…
Fazit: was ist denn nun ein Photon?
Es gibt also unterschiedliche Zustände des em-Quantenfeldes, die man alle irgendwie als “Photon” bezeichnen kann:
a. Eine Anregung des em-Feldes mit Energie hν
b. Jede Überlagerung von Anregungen unterschiedlicher Frequenz mit Teilchenzahl 1, auch wenn die Energie dadurch beliebig ungenau definiert sein kann.
c. Eine Überlagerung von Zuständen zu einem Wellenpaket mit mittlerer Energie hν. (Diese Definition dürfte für die meisten praktischen Probleme, wenn es etwa um Lichtabsorption o.ä. geht, die praktischste sein.)
d. Ein “Teil” eines Zustandes analog zu a-c mit einer höheren Photonenzahl. Beispielsweise ist der Zustand oben unter 2. ja ein 2-Photon-Zustand, er besteht also konzeptionell aus zwei Photonen mit Energie hν. Genauso können wir einen “Teil” eines Wellenpakets, das einen drei-Photonen-Zustand beschreibt, als “ein Photon” ansehen.
Schließlich gibt es noch e. für virtuelle Photonen, aber die habe ich hier ja nicht weiter diskutiert, ich liste sie nur der Vollständigkeit halber.
Alle Überlegungen hier habe ich aus der Sicht der Quantenfeldtheorie angestellt, also mit dem Fokus auf die grundlegende Physik. Wenn ihr in einer Quantenoptik-Abteilung nachfragt, bekommt ihr dort möglicherweise noch andere Antworten zu hören (siehe dazu den OPN-Trends-Artikel), die sich zum Beispiel mit der Frage befassen, ob man Photonen auch ähnlich wie Elektronen mit Hilfe von Wellenfunktionen beschreiben kann. (Ich habe dabei noch insofern vereinfacht, als wir auch noch unterschiedliche Richtungen des E-feldes angucken könnten – das führt dann zur Polarisation. Damit gibt es dann noch mehr Möglichkeiten, überlagerte Zustände zu basteln, aber prinzipiell kommt nichts Neues mehr hinzu.)
So oder so seht ihr, dass die Frage “Was ist ein Photon?” kniffliger ist als man anfangs meinen könnte. Ob man deswegen – wie von Lamb vorgeschlagen – Lizenzen vergeben sollte, ohne die man das Wort nicht verwenden darf, weiß ich nicht. Aber ganz so einfach, wie man nach der Wiki-Definition denken könnte, ist die Sache nicht.
Optics and Photonics News, Oct 2003, “OPN Trends—The Nature of Light: What Is a Photon?“















Kommentare (136)