Im letzten Teil hatte ich den Propagator erklärt, der etwas darüber sagt, wie sich Störungen des Feldes (“Ich spüre eine Erschütterung der Macht”) ausbreiten. Dieser Propagator hat direkt etwas mit den Teilchen zu tun, die wir beobachten, aber um das ausführlich zu erklären, muss ich etwas ausholen.
Wer die Serie aufmerksam verfolgt, der wundert sich vielleicht schon die ganze Zeit über eins: Je nachdem, wie es mir in den Kram passt, argumentiere ich manchmal mit ebenen Wellen, manchmal dagegen mit Propagatoren. Wie passt das zusammen? Ist das nicht ein Widerspruch – mal haben wir Feldanregungen, die sich von einem Punkt aus ausbreiten, mal haben wir Wellen, die über den ganzen Raum ausgebreitet sind. Kurz habe ich das schon einmal erklärt, aber es lohnt sich, darauf etwas genauer einzugehen.
Das Geheimnis, das dahinter steckt, sind die berühmten Fouriertransformationen. Die sind in der Physik nahezu allgegenwärtig, weil sie es erlauben, sehr viele Phänomene mit Hilfe von Wellen zu beschreiben.
Die Kernaussage, die hinter den Fouriertransformationen steckt, ist ziemlich einfach zu formulieren, deswegen muss sie auch nicht in irgendeinen fiesen Formelteil1: Jede mathematisch hinreichend brave Funktion kann man als Summe von (meist unendlich vielen) ebenen Wellen darstellen.
1den ich mir hier auch spare – Erklärungen von Fourier-Transformationen gibt es wie Sand am Meer und die von euch, die diese abgefahrenen Teile mit partiellen Ableitungen und so Zeugs lesen können, schütteln Fourier-Trafos doch eh aus dem Ärmel, oder? (Falls nicht, beschwert euch in den Kommentaren…)
Um euch das ein bisschen anschaulich zu machen, vereinfache ich die Aussage ein wenig und beschränke mich erst einmal auf Funktionen, die periodisch sind, sich also wiederholen (das heißt, wir betrachten erst mal Fourier-Reihen). Dafür gibt es viele hübsche Bilder bei Wikipedia, die dem faulen Blogger das Leben erleichtern.
Stellt euch als erstes eine Rechteckfunktion vor, so wie diese:
Das sieht schon ein bisschen wie eine Welle aus, nur ist es ziemlich eckig. Wie können wir so eine Funktion mit Wellen annähern? Das zeigt dieses Bild (ebenfalls von Wikipedia geklaut):
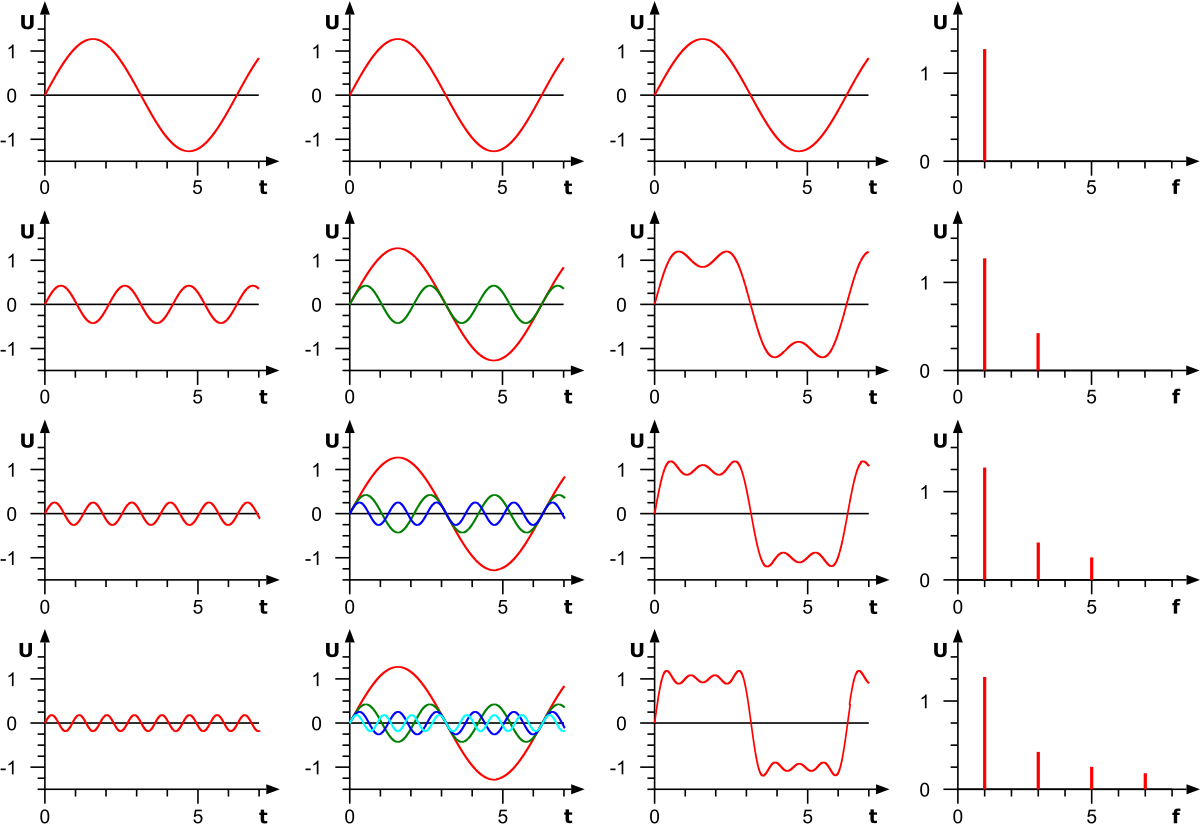
Von René Schwarz – Eigenes Werk, SVG Version of File:Fouriersynthese.png, CC BY-SA 3.0, Link
Nicht erschrecken, wenn es kompliziert aussieht, ist es gar nicht. In der oberen Zeile seht ihr die allererste Näherung eines Rechtecks: Durch eine Welle (oder mathematisch etwas präziser eine Sinusfunktion) mit derselben Wellenlänge. Der Sinus ist aber zu “rund”, wir müssen dafür sorgen, dass er schärfere Kanten bekommt. Damit fangen wir in der zweiten Zeile an: Wenn wir eine weitere Welle mit kürzerer Wellenlänge (linke Spalte) nehmen, und die zu unserem Sinus addieren (zweite Spalte), dann ergibt sich etwas, das schon ein bisschen rechteckiger aussieht (dritte Spalte). Nehmen wir noch eine Welle (dritte Zeile) hinzu, wird’s noch besser, und dann in der vierten Zeile sieht es schon ganz anständig aus, oder?
Die ganz rechte Spalte zeigt übrigens, welche Frequenzen jeweils verwendet wurden – je kürzer die Wellenlänge, desto höher die Frequenz. Ihr seht, dass nur bestimmte Frequenzen (und Wellenlängen) verwendet werden – das liegt daran, dass die Funktion periodisch ist, also müssen auch die verwendeten ebenen Wellen zu dieser Periode passen.
Ganz ähnlich kann man auch andere Funktionen annähern, hier zum Beispiel ein Sägezahn Dreieck:
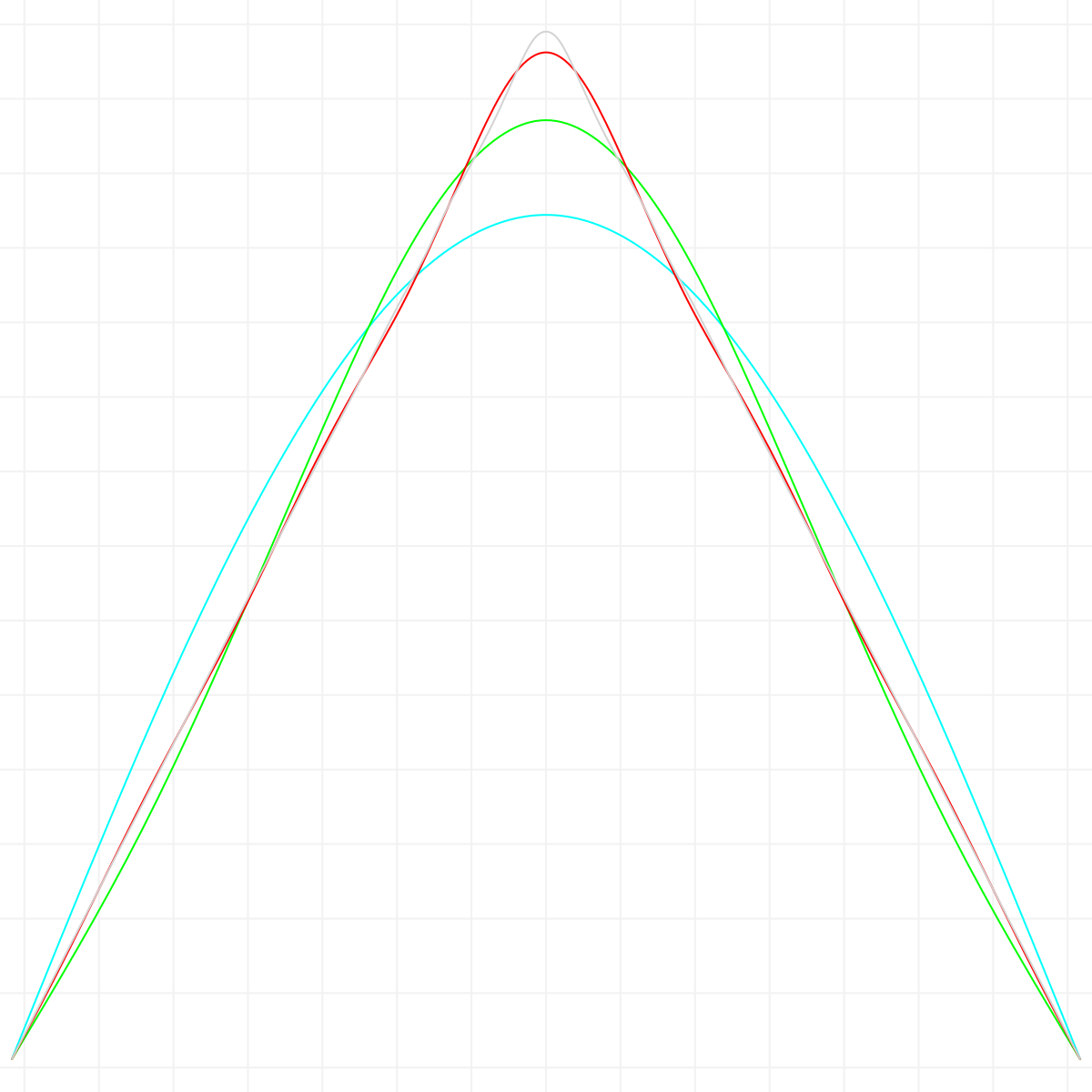
Von TieR0815 – Eigenes Werk, CC BY 3.0, Link
Wenn ihr Lust habt, das selbst auszuprobieren, dann findet ihr hier ein schickes Java-Applet zum Spielen.
Aus dem Alltag kennt ihr das übrigens auch, nämlich im Bereich der Musik. Vergleicht ein Klavier und eine Querflöte, die beide den gleichen Ton (sagen wir das eingestrichene A) spielen. Dieser Ton hat ja eine bestimmte Frequenz. Wie kommt es dann, dass die beiden Instrumente so verschieden klingen, obwohl sie doch denselben Ton spielen? Das liegt an den Obertönen: Der Grundfrequenz von 440Hertz sind weitere, höhere Frequenzen überlagert. Diese Überlagerung ist für den charakteristischen Ton verantwortlich. Da ich hier aber nicht die Serie “Musiktheorie für alle” schreibe (dafür wäre ich auch ungefähr so geeignet wie ein Kanu zum Radfahren), verweise ich auf den netten und gut bebilderten Artikel bei Wikipedia und ein weiteres nettes Applet.






Kommentare (13)