Die Physik wird ja von Formeln dominiert – einfache anschauliche Bildchen oder Überlegungen ohne jede Formel allein reichen nicht aus, um die Welt wirklich korrekt zu verstehen oder Dinge vorherzusagen. Aber ganz ohne solche Anschauungen geht es natürlich auch nicht, denn die Anschauung liefert Ideen, wie man Probleme lösen kann. Und deswegen ist es immer gut, wenn man Formeln auch noch einmal mit Worten beschreibt.
Leider kann das auch schiefgehen – und dann bekommt man Beschreibungen, die anschaulich nicht gut funktionieren, die aber scheinbar das wiedergeben, was die Formeln sagen.
Ein Beispiel dafür ist – zumindest meiner Ansicht nach – das sogenannte “Heisenberg-Bild” in der Quantenmechanik. Ich habe eigentlich nie verstanden, wie man es anschaulich interpretieren soll, denn mit der Erklärung, die in jedem Buch steht, konnte ich nie viel anfangen. Vor kurzem habe ich gemerkt, woran das liegt: Die anschauliche Beschreibung des Heisenbergbilds ist extrem irreführend, wenn nicht sogar schlicht falsch.
WARNUNG Das, was ich in diesem Text über die Interpretation des Heisenbergbilds schreibe, ist wie gesagt meine eigene, persönliche Überlegung. Sie steht im Widerspruch zu dem, was man in den meisten Büchern lesen kann (auch wenn die Formeln und Rechnungen sich nicht ändern), und es ist vermutlich keine gute Idee, wenn ihr das so während eurer Physikprüfung erzählt. Und noch eine zweite Warnung hinterher: Das Heisenbergbild ist ein mathematischer Formalismus aus den Tiefen der Quantenmechanik. Ich habe mir zwar Mühe gegeben, ein bisschen das drumherum zu erklären, aber ich vermute, dass dieser Text nur für diejenigen von euch verständlich ist, die irgendwann mal ein QM-Buch gelesen oder eine Vorlesung besucht haben.
Fangen wir erst mal mit dem Schrödinger-Bild an, das ist das Bild, das die meisten wohl zuerst kennenlernen und das typischerweise auch in populären Darstellungen verwendet wird. Im Schrödingerbild ist das Elektron zu jedem Zeitpunkt in einem bestimmten Zustand, den man mit 
Formal-mathematisch kann man die zeitliche Entwicklung der Wellenfunktion mit Hilfe des sogenannten “Zeitentwicklungsoperators” beschreiben, den nenne ich U(t). Es gilt also
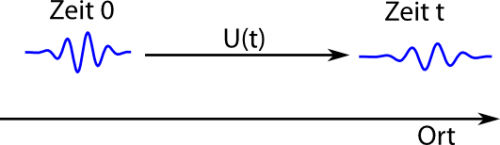
U(t) macht also aus dem Zustand zur Zeit 0 den Zustand zur Zeit t.
Als Beispiel hier ein Wellenpaket, das ein Elektron an einem Ort zur Zeit 0 repräsentiert. Das Elektron fliegt von links nach rechts, so dass das Wellenpaket sich verschiebt (dabei läuft es etwas auseinander) und später dann an einem anderen Ort lokalisiert ist:
Zustände selbst kann man in der QM nicht beobachten – beobachten kann man nur Messwerte von bestimmten Größen (man kann zum Beispiel den Ort eines Elektrons messen). Da in der QM der Zufall eine wichtige Rolle spielt, kann man den Ort mit Hilfe des Zustands normalerweise nicht eindeutig vorhersagen – man kann nur eine Wahrscheinlichkeit dafür angeben, einen bestimmten Wert zu messen. Insbesondere interessiert man sich für den Erwartungswert – also den Mittelwert einer Messgröße bei vielen Messungen. Für den gilt – wenn man ihn zur Zeit t messen will – die Formel
Dabei ist A die mathematische Beschreibung der Messgröße (wie die aussieht, muss uns hier nicht kümmern) und 
Statt einen solchen Erwartungswert zu messen, kann man auch andere Sache mit einem Zustand machen. Stellen wir uns beispielsweise ein Elektron vor, dass auf eine Wand zufliegt und von der reflektiert wird. Auch diese Wirkung der Wand können wir mathematisch beschreiben – wenn die Wand zur Zeit t auf das Elektron wirkt, dann hat es hinterher einen anderen Zustand als vorher (weil es jetzt in eine andere Richtung fliegt). Mathematisch kann man das so beschreiben (W ist der “Wand-Operator” – Operatoren sind mathematische Objekte, die was mit einem Zustand anstellen):
Nach der Reflexion von der Wand ist das Elektron also in einem neuen Zustand. (Ich tue hier so, als ginge die Reflexion unendlich schnell – das ist zwar nicht realistisch, aber als Vereinfachung nützlich.) Graphisch können wir uns das so vorstellen:
Kommentare (12)