StartseiteHier wohnen Drachen

Schrödinger-Bild, Heisenberg-Bild und die Anschauung in der Physik

Von / 13. Juni 2015 / 12 Kommentare / Seite 2 von 3 / Auf einer Seite lesen
Mehr

heisenberg2

(Hinweis: Man kann sich hier fragen, warum die Wechselwirkung mit der Wand nicht schon im Zeitentwicklungoperator mit drin ist. Das ist eine Frage der Bequemlichkeit – man könnte das tun, dann ändert sich der Zeitentwicklungoperator entsprechend. Oft ist es aber nützlich, die “ungestörte” Zeitentwicklung und den Einfluss von zum Beispiel einer Wand (oder einer Messung oder sonst etwas) zu trennen.)

So weit, so gut. Man kann die Gleichungen aber auch etwas anders anschauen. Dazu nehmen wir erstmal die Gleichung von oben für den Erwartungswert:
\langle \psi(t)| A |\psi(t)\rangle
Jetzt bauen wir in die Gleichung die Tatsache ein, dass sich der Zustand zur Zeit t ja aus dem zur Zeit Null entwickelt hat, wir setzen also den Zeitentwicklungsoperator ein:
\langle \psi(0)|U^\dag(t) A U(t)|\psi(0)\rangle
Links muss man dabei auch den Operator “konjugieren”, dafür steht das kleine Kreuz oben rechts. (Ich spare mir, die Details zu erklären – wenn ihr ne QM-Vorlesung besucht habt, kennt ihr die, wenn nicht, braucht ihr sie auch nicht zu kennen, um das, was gleich kommt, zu verstehen.)
Als nächstes bastle ich in die Gleichung oben eine Klammer ein:
\langle \psi(0)| (U^\dag(t) A U(t))|\psi(0)\rangle
Oben hatte ich ja gesagt, dass A nicht von der Zeit abhängt. Wir können jetzt aber in dieser Formel die Zeitabhängigkeit vom Zustand auf die Messgröße abwälzen und A(t) = (U^\dag(t) A U(t)) schreiben.
Dann sieht unsere Formel für den Erwartungswert so aus:
\langle \psi(0)| A(t)|\psi(0)\rangle
Mathematisch ist das erst mal kein Problem, wie ihr seht, es ist lediglich eine andere Schreibweise. Diese Schreibweise ist gerade das sogenannte “Heisenberg-Bild”.

Wir können dasselbe auch mit unserem Wandoperator machen und W(t) = (U^\dag(t) W U(t)) definieren und diesen Operator dann auf |\psi(t)\rangle loslassen:
| W(t) |\psi(0)\rangle = (U^\dag(t) W U(t)) |\psi(0)\rangle = U^\dag(t) |\phi(t)\rangle
Dabei habe ich die Gleichungen von oben eingesetzt – U entwickelt den Zustand von der Zeit Null nach t, dann wirkt W drauf und macht aus dem einen Zustand den anderen. Für den Zustand nach Anwendung von W kommt jetzt nicht |\phi(t)\rangle heraus, sondern es steht noch ein U^\dag davor. Was bedeutet das?

Um das herauszubekommen, muss man sich angucken, wie der Zeitentwicklungsoperator mathematisch funktioniert. (Zum Beispiel auf der entsprechenden Wiki-Seite, wo ihr die meisten der Formeln hier wiederfinden könnt.) Dann sieht man, dass U^\dag, angewandt auf einen Zustand zur Zeit t, zurückrechnet auf den entsprechenden Zustand zur Zeit 0. Es ist also
U^\dag|\psi(t)\rangle = |\psi(0)\rangle
Also: Wenn das U^\dag rechts von einem konjugierten Zustand steht, dann transportiert es diesen Zustand in der Zeit vorwärts, wenn es aber links von einem Zustand zur Zeit t steht, dann rechnet es den Zustand zurück.

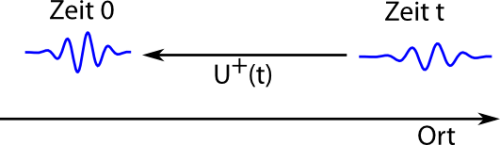
heisenberg3
Damit sehen wir jetzt, was nach Anwendung des Wandoperators im Heisenbergbild insgesamt passiert:
| W(t) |\psi(0)\rangle = |\phi(0)\rangle

Im Heisenbergbild ist es also so, dass man alle Zeitabhängigkeit auf die Operatoren abwälzt – die Zustände selbst haben keine Zeitabhängigkeit. In vielen Büchern wird das sogar so formuliert, dass gesagt wird “Der Zustand im Heisenbergbild ist eingefroren”.

Und genau das ist der Punkt, mit dem ich immer meine Probleme hatte – ich sehe zwar mathematisch leicht ein, wie das Heisenbergbild funktioniert, aber wenn ich ein Elektron betrachte, dass zur Zeit Null in einem Zustand ist, ist es dann wirklich sinnvoll zusagen, dass sich der Zustand nicht ändert? Wenn es zum Beispiel bei t=0 bei Alpha Centauri lokalisiert war und jetzt hier auf der Erde ist, ergibt es dann Sinn zusagen, dass der Zustand des Elektrons immer noch bei Alpha Centauri eingefroren ist? Ist das nicht eine seltsame Verwendung des Begriffs “Zustand”? Mit dieser Art der Formulierung konnte ich nie etwas anfangen und hatte deswegen immer Probleme, mir das Heisenberg-Bild anschaulich zu machen.

1 / 2 / 3
Stichworte: , , ,
Mehr

Kommentare (12)

  1. #1 alex
    13. Juni 2015

    In der kanonischen Formulierung der Quantenfeldtheorie finde ich das Heisenbergbild auch deshalb passend, weil die Feldoperatoren dann von Ort und Zeit abhängen. Im Schrödingerbild sind die Zustände zeitabhängig und die Operatoren ortsabhängig. Vor allem für relativistische Theorien finde ich das sehr unschön.

    Und in der normalen Einteilchen-Quantenmechanik spricht dasselbe Argument für das Schrödingerbild.

  2. #2 MartinB
    13. Juni 2015

    @alex
    “weil die Feldoperatoren dann von Ort und Zeit abhängen.”
    Das ist ein teil meines Problems – warum sollen die Feldoperatoren den Zustand eines Quantenfeldes beschreiben? (Geht ja auch anders, man kann ja auch QFT im Schrödingerbild betreiben.) Und mich hat immer gestört, dass man die Operatorfelder analog zur Lösung in der relativistischen QM herleitet und dann sagt” Hoppla, die Koeffizienten sind jetzt Operatoren” – und ich habe mich immer gefragt: “Wo bleibt denn dann die Freiheit, die ich vorher in der Lösung hatte – erst hatte ich einen Satz beliebiger Fourier-Koeffizienten, jetzt habe ich nen Satz eindeutig bestimmter Operatoren.” Antwort ist natürlich, dass die Freiheit im Zustand steckt, auf den die Operatoren wirken, und auch da macht es für mich deutlich mehr Sinn, den als “Anfangszustand” zu betrachten.
    Vielleicht ist das aber auch mein ganz persönliches Verständnisproblem…

  3. #3 dgbrt
    13. Juni 2015

    Ich tue mich nach einem 30 Jahre zurückliegenden und einem erfolgreichen Vor-Diplom aber nicht abgeschlossenem Physik-Studium schwer diese verkürzten Formeln zu begreifen.

    Die Frage hier ist die Abhängigkeit einer Zustandsgleichung von der Zeit. Meiner Ansicht ist die Frage richtig, aber es ist nicht die Zeit, sondern es sind räumlich zu lokalisierende Einflüsse, die den Zustand eines Elektrons beeinflussen.

    Ein Elektron, welches vom Alpha Centauri zu uns fliegt, ändert im Laufe der vier Jahre (annähernd Lichtgeschwindigkeit angenommen) seinen Zustand nicht, solange es nicht mit anderen Teilchen interagiert. Aber das wird es während der langen Reise natürlich machen, das hängt aber nicht von der Zeit sondern der Umgebung ab.

    Somit ist die Vereinfachung auf den Faktor Zeit bei Weitem nicht ausreichend, um die komplexen Strukturen unseres Universums erklären zu können. Ereignisse benötigen Zeit (wegen der endlichen Lichtgeschwindigkeit), um einen anderen Körper beeinflussen zu können. Somit hängt alles von der Zeit ab, aber die Wirkung kommt von andern Ereignissen.

  4. #4 MartinB
    14. Juni 2015

    @dgbrt
    “ändert im Laufe der vier Jahre (annähernd Lichtgeschwindigkeit angenommen) seinen Zustand nicht,”
    Das hängt sicher davon ab, was man als “Zustand” auffasst – in meinen Augen gehört der Ort, wo das Elektron ist, auch zum Zustand.

    “Somit ist die Vereinfachung auf den Faktor Zeit bei Weitem nicht ausreichend, um die komplexen Strukturen unseres Universums erklären zu können.”
    Darum geht’s in diesem Artikel ja auch nicht.

  5. #5 Dr. Webbaer
    14. Juni 2015

    Mal philosophisch und naturwissenschaftlich laienhaft angemerkt hierzu:

    Und genau das ist der Punkt, mit dem ich immer meine Probleme hatte – ich sehe zwar mathematisch leicht ein, wie das Heisenbergbild funktioniert, aber wenn ich ein Elektron betrachte, dass zur Zeit Null in einem Zustand ist, ist es dann wirklich sinnvoll zusagen, dass sich der Zustand nicht ändert?

    Wenn dieser Zustand oder “Zustand” über probalistische Theoretisierung verstanden wird, ändert sich dieser Zustand oder “Zustand” deshalb nicht, weil er sich ändernd ist und (nur) probalistisch beschrieben werden kann.
    KA, ob dieser Hinweis an dieser Stelle irgendwie hilfreich ist, “geschnüffelt” wird hier zumindest realistisches [1] Sachverständnis.
    Dieses ist letztlich aus konstruktivistischer Sicht abzulehnen.

    MFG
    Dr. W

    [1]
    Ein Pleonasmus, korrekt, Sachen und Sachverhalte, Realismus, finden für einige, gerade Physiker sind gemeint, ganz bevorzugt in oder auf bestimmten Schichten des Seins statt.

  6. #6 Niels
    14. Juni 2015

    Darüber habe ich bisher noch nie nachgedacht. Operatoren sind im Heisenbergbild zeitabhängig, Zustände dafür nicht. Mehr Hirnschmalz hab ich da nie investiert. 😉

    Ich sehe jedenfalls nicht, was an deiner Interpretation falsch sein könnte. Ist mathematisch auch ziemlich einfach zu erkennen, oder?
    Hab ich so allerdings wirklich noch nie gelesen.

    Die Reaktionen im physicsforum finde ich dagegen ziemlich verblüffend. Eigentlich kennen sich die dortigen Kommentatoren ja extrem gut aus. Hier haben sie aber anscheinend überhaupt nicht verstanden, worum es dir geht und reden mehr oder weniger vollständig am Thema vorbei.
    Oder ist das nur mein Eindruck?

  7. #7 Dr. Webbaer
    14. Juni 2015

    @ Niels :

    Operatoren sind im Heisenbergbild zeitabhängig, Zustände dafür nicht.

    Geht Richtung Dingbeschreibung:

    Why is any object we don’t understand always called a thing? [“Leonard McCoy”]

    Dinge und ihnen womöglich zuzuschreibende Funktionalität sind physikalisch zu theoretisieren, wobei es immer um Zustände und Operatoren oder Wirkungen zu gehen hat, gerne auch um: intrinsische.
    ‘Zeitabhängigkeit’, was ist Zeit genau außer dem Ändern von Zustand, dessen Feststellung erkennenden Subjekten obliegt?, rundet das dbzgl. Vorhaben dann sozusagen ab.

    MFG + schönen Sonntag noch,
    Dr. W

  8. #8 MartinB
    14. Juni 2015

    @Niels
    Ja, ich hab’s bisher auch immer so geschluckt, aber ich fand es eben immer extrem unanschaulich, von einem zeitunabhängigen Zustand zu reden – entweder es ist zeitabhängig, oder es sollte nicht “Zustand” heißen, weil Zustände sich
    nun mal ändern. Aber gerade in der QFT kam ich mit der Vorstellung “Zustände sind zeitunabhängig” nie richtig klar – insbesondere, weil die Wirkung von Operatoren die Zustände ja ändert. Dank der Uminterpretation sehe ich jetzt klarer, wie das funktioniert.

    Ich denke auch nicht, dass meine Interpretation falsch sein kann, sind ja dieselben Gleichungen.

    “Oder ist das nur mein Eindruck?”
    Nein, so ging es mir auch. Aber generell ist das Physikforum (so gut die Antworten oft sind) sehr stark auf Formalismus ausgerichtet und anschauliche Erklärungen gibt es dort eher selten. Dieselbe Erfahrung habe ich mit meinen Fragen zur ART gemacht.

  9. #9 Lutz Donnerhacke
    15. Juni 2015

    Danke, Deine Erklärung ist nachvollziehbar und hilfreich.

    Das Bild “Was passiert, wenn ich die Ausgangswerte ändere?” ist ziemlich treffend. Es fokussiert den Kopf auf den wichtigen Gedanken: “Was will ich mit dem Formalismus erreichen? Wofür macht man diesen Ansatz?”

    Also herzlichen Dank dafür.

  10. #10 MartinB
    15. Juni 2015

    @Lutz
    Danke, freut mich, dass es noch jemandem hilft – ist immer ein komisches Gefühl, wenn man selbst den Eidnruck hat, eine Idee lässt einen Riesen-Knoten platzen und keine andere kann’s nachvollziehen.

  11. #11 Phero
    24. Juli 2015

    Ehrlich gesagt, verstehe ich persönlich wirklich nicht das Neue an deiner Anschauung. Genau das habe ich immer unter “eingefrorenen” Zuständen verstanden – man nehme einen Zustand (eben das Psi_0) und schiebe die gesamte Zeitahängigkeit in den Operator.
    Mir persönlich war – in der nichtrelativistischen QM – nie die Nützlichkeit des Heisenbergbildes klar. DIe Erklärung mit den verschiedenen Anfangszuständen, für die wir nur einmalig den Operator A(t) ausrechnen müssen, stimmt auch nur bedingt. Immerhin ergeben verschiedene Energie im Anfangszustand verschiedene Zeitentwicklungen. Derzeit sehe ich das Heisenbergbild eher als praktische Herleitung zum Diracbild an, welches der Intuition meiner Ansicht nach extrem zu Gute kommt.

  12. #12 MartinB
    24. Juli 2015

    @Phero
    “Ehrlich gesagt, verstehe ich persönlich wirklich nicht das Neue an deiner Anschauung.”
    Das neue ist nur, dass ich explizit sage “die fehlende Zeitabhängigkeit kommt schlicht daher, dass ich immer auf den Anfangszustand zurückrechne”; während man normalerweise sagt, dass der Zustand tatsächlich “eingefroren” ist und sich zeitlich nicht ändert. Ich sage, dass der sich schon ändern kann, dass man das nur einfach nicht anguckt, weil man eben zurückrechnet.

    “DIe Erklärung mit den verschiedenen Anfangszuständen, für die wir nur einmalig den Operator A(t) ausrechnen müssen, stimmt auch nur bedingt. Immerhin ergeben verschiedene Energie im Anfangszustand verschiedene Zeitentwicklungen.”
    Schon – aber wenn du dir z.B. mal die Original-paper von Heisenberg oder Jordan anguckst, dann wird da überhaupt nicht über die Zustände geredet, die rechnen nur mit den Operatoren.. Insofern ist das schon praktisch.