StartseiteHier wohnen Drachen

Schrödinger-Bild, Heisenberg-Bild und die Anschauung in der Physik

Von / 13. Juni 2015 / 12 Kommentare / Seite 3 von 3 / Auf einer Seite lesen
Mehr

Hinzu kommt noch etwas anderes: Wenn ich sage, dass im Heisenberg-Bild |\psi(0)\rangle den Zustand des Elektrons zu jedem Zeitpunkt beschreibt (weil ja die ganze Zeitabhängigkeit auf die Operatoren abgewälzt wurde), dann ist ein Zustand im Heisenbergbild ganz was anderes als ein Zustand im Schrödingerbild. Eigentlich müsste man dann alles, was man sich im Schrödingerbild für Zustände in der QM überlegt hat, erst mal überprüfen, ob es immer noch gilt.

Aber dankenswerterweise hatte ich neulich eine Idee, wie ich die Formeln anders interpretieren kann und das ganze einen Sinn ergibt – zumindest für mich, meldet euch bitte in den Kommentaren, wenn euch diese Uminterpretation auch etwas nützt, dann weiß ich wenigstens, dass ich nicht allein bin. (Und sagt auch gern, wenn ihr meine Erklärung nicht mögt oder gar für fehlerhaft haltet, denn wie gesagt garantiere ich für nichts….)

Dazu nehme ich das Schrödingerbild beim Wort. |\psi(t)\rangle beschreibt den Zustand des Elektrons zur Zeit t, Punkt, egal was der olle Heisenberg dazu sagt (wobei die Formulierung mit den “eingefrorenen Zuständen” sicherlich nicht von Heisenberg stammt…).

Wenn ich das so annehme, was tut dann das Heisenbergbild? Da taucht ja in den Formeln immer nur |\psi(0)\rangle auf, nie |\psi(t)\rangle. Das Heisenbergbild rechnet also alles, was es rechnet, so um, dass es sich immer auf den Anfangszustand bezieht. Schaut noch einmal auf die Formel für den Erwartungswert:
\langle \psi(0)| A(t)|\psi(0)\rangle

Was das A tut ist, dass es zunächst mit dem Zeitentwicklungsoperator aus dem Anfangszustand den aktuellen berechnet, dann darauf A wie im Schrödingerbild anwendet, und dann den neuen Zustand wieder zum Anfang zurücktransportiert (Ich kann den konjugierten Zeitentwicklungsoperator ja auch nach rechts wirken lassen und damit den Zustand wieder zurückrechnen.)

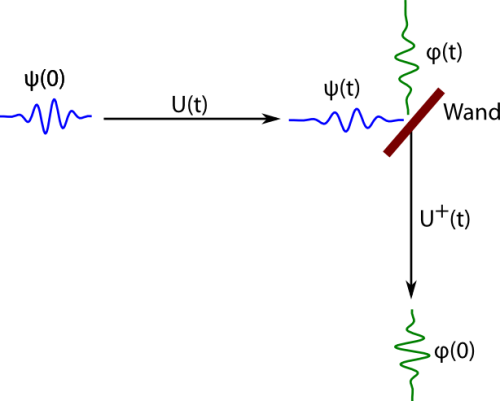
Genauso funktioniert es mit dem Wandoperator im Heisenbergbild:
| W(t) |\psi(0)\rangle = |\phi(0)\rangle
Der transportiert ebenfalls erst den Zustand zeitlich nach t, dann wird der Zustand zu der Zeit an der Wand reflektiert, und dann wird in der Zeit zurückgerechnet. Der Wandoperator rechnet also den fiktiven Zustand |\phi(0)\rangle aus – den Zustand, den das Elektron zur Zeit 0 hätte haben müssen, wenn es zur Zeit t im Zustand |\phi(t)\rangle ist und sich in diesen Zustand entwickelt hätte, ohne dass die Wand da wäre:

heisenberg4

Im Heisenbergbild sind die Zustände nicht “eingefroren” – stattdessen betrachte man einfach nur immer den Zustand, der zur Zeit t=0 hätte vorliegen müssen, damit sich aus diesem der aktuelle Zustand entwickelt (so wie eben bei der Wandreflexion). (Wie oben gesagt bekommen wir beim Zurückrechnen hier einen anderen Zustand als wir tatsächlich zur Zeit Null hatten, weil wir den Einfluss des Wandoperators nicht mit in der Zeitentwicklung berücksichtigt haben.)

Damit sieht man auch, warum das Heisenbergbild praktisch sein kann: Interessiert man sich für eine bestimmte Messgröße, dann kann man im Heisenbergbild ein für alle Mal das A(t) ausrechnen und dann auf unterschiedliche Anfangszustände anwenden- die ganze Zeitentwicklung hat man damit schon erledigt. So macht man es zum Beispiel auch in der Quantenfeldtheorie, die gern (in der “kanonischen Formulierung”) im Heisenbergbild formuliert wird.

Ich weiß nicht, wer zum ersten Mal die Formulierung mit den “eingefrorenen Zuständen” aufgebracht hat – aber meiner Ansicht nach ist sie eher verwirrend als hilfreich, und man sollte lieber sagen, dass das Heisenbergbild immer auf (eventuell fiktive) Anfangszustände zurückrechnet.

                      

Ich habe das mit dem Heisenbergbild auch beim physicsforum zu diskutieren versucht – dort stieß meine Idee auf wenig Begeisterung. Insofern übernehme ich keine Haftung, dass das hier für irgendwen außer mir Sinn ergibt.

1 / 2 / 3
Stichworte: , , ,
Mehr

Kommentare (12)

  1. #1 alex
    13. Juni 2015

    In der kanonischen Formulierung der Quantenfeldtheorie finde ich das Heisenbergbild auch deshalb passend, weil die Feldoperatoren dann von Ort und Zeit abhängen. Im Schrödingerbild sind die Zustände zeitabhängig und die Operatoren ortsabhängig. Vor allem für relativistische Theorien finde ich das sehr unschön.

    Und in der normalen Einteilchen-Quantenmechanik spricht dasselbe Argument für das Schrödingerbild.

  2. #2 MartinB
    13. Juni 2015

    @alex
    “weil die Feldoperatoren dann von Ort und Zeit abhängen.”
    Das ist ein teil meines Problems – warum sollen die Feldoperatoren den Zustand eines Quantenfeldes beschreiben? (Geht ja auch anders, man kann ja auch QFT im Schrödingerbild betreiben.) Und mich hat immer gestört, dass man die Operatorfelder analog zur Lösung in der relativistischen QM herleitet und dann sagt” Hoppla, die Koeffizienten sind jetzt Operatoren” – und ich habe mich immer gefragt: “Wo bleibt denn dann die Freiheit, die ich vorher in der Lösung hatte – erst hatte ich einen Satz beliebiger Fourier-Koeffizienten, jetzt habe ich nen Satz eindeutig bestimmter Operatoren.” Antwort ist natürlich, dass die Freiheit im Zustand steckt, auf den die Operatoren wirken, und auch da macht es für mich deutlich mehr Sinn, den als “Anfangszustand” zu betrachten.
    Vielleicht ist das aber auch mein ganz persönliches Verständnisproblem…

  3. #3 dgbrt
    13. Juni 2015

    Ich tue mich nach einem 30 Jahre zurückliegenden und einem erfolgreichen Vor-Diplom aber nicht abgeschlossenem Physik-Studium schwer diese verkürzten Formeln zu begreifen.

    Die Frage hier ist die Abhängigkeit einer Zustandsgleichung von der Zeit. Meiner Ansicht ist die Frage richtig, aber es ist nicht die Zeit, sondern es sind räumlich zu lokalisierende Einflüsse, die den Zustand eines Elektrons beeinflussen.

    Ein Elektron, welches vom Alpha Centauri zu uns fliegt, ändert im Laufe der vier Jahre (annähernd Lichtgeschwindigkeit angenommen) seinen Zustand nicht, solange es nicht mit anderen Teilchen interagiert. Aber das wird es während der langen Reise natürlich machen, das hängt aber nicht von der Zeit sondern der Umgebung ab.

    Somit ist die Vereinfachung auf den Faktor Zeit bei Weitem nicht ausreichend, um die komplexen Strukturen unseres Universums erklären zu können. Ereignisse benötigen Zeit (wegen der endlichen Lichtgeschwindigkeit), um einen anderen Körper beeinflussen zu können. Somit hängt alles von der Zeit ab, aber die Wirkung kommt von andern Ereignissen.

  4. #4 MartinB
    14. Juni 2015

    @dgbrt
    “ändert im Laufe der vier Jahre (annähernd Lichtgeschwindigkeit angenommen) seinen Zustand nicht,”
    Das hängt sicher davon ab, was man als “Zustand” auffasst – in meinen Augen gehört der Ort, wo das Elektron ist, auch zum Zustand.

    “Somit ist die Vereinfachung auf den Faktor Zeit bei Weitem nicht ausreichend, um die komplexen Strukturen unseres Universums erklären zu können.”
    Darum geht’s in diesem Artikel ja auch nicht.

  5. #5 Dr. Webbaer
    14. Juni 2015

    Mal philosophisch und naturwissenschaftlich laienhaft angemerkt hierzu:

    Und genau das ist der Punkt, mit dem ich immer meine Probleme hatte – ich sehe zwar mathematisch leicht ein, wie das Heisenbergbild funktioniert, aber wenn ich ein Elektron betrachte, dass zur Zeit Null in einem Zustand ist, ist es dann wirklich sinnvoll zusagen, dass sich der Zustand nicht ändert?

    Wenn dieser Zustand oder “Zustand” über probalistische Theoretisierung verstanden wird, ändert sich dieser Zustand oder “Zustand” deshalb nicht, weil er sich ändernd ist und (nur) probalistisch beschrieben werden kann.
    KA, ob dieser Hinweis an dieser Stelle irgendwie hilfreich ist, “geschnüffelt” wird hier zumindest realistisches [1] Sachverständnis.
    Dieses ist letztlich aus konstruktivistischer Sicht abzulehnen.

    MFG
    Dr. W

    [1]
    Ein Pleonasmus, korrekt, Sachen und Sachverhalte, Realismus, finden für einige, gerade Physiker sind gemeint, ganz bevorzugt in oder auf bestimmten Schichten des Seins statt.

  6. #6 Niels
    14. Juni 2015

    Darüber habe ich bisher noch nie nachgedacht. Operatoren sind im Heisenbergbild zeitabhängig, Zustände dafür nicht. Mehr Hirnschmalz hab ich da nie investiert. 😉

    Ich sehe jedenfalls nicht, was an deiner Interpretation falsch sein könnte. Ist mathematisch auch ziemlich einfach zu erkennen, oder?
    Hab ich so allerdings wirklich noch nie gelesen.

    Die Reaktionen im physicsforum finde ich dagegen ziemlich verblüffend. Eigentlich kennen sich die dortigen Kommentatoren ja extrem gut aus. Hier haben sie aber anscheinend überhaupt nicht verstanden, worum es dir geht und reden mehr oder weniger vollständig am Thema vorbei.
    Oder ist das nur mein Eindruck?

  7. #7 Dr. Webbaer
    14. Juni 2015

    @ Niels :

    Operatoren sind im Heisenbergbild zeitabhängig, Zustände dafür nicht.

    Geht Richtung Dingbeschreibung:

    Why is any object we don’t understand always called a thing? [“Leonard McCoy”]

    Dinge und ihnen womöglich zuzuschreibende Funktionalität sind physikalisch zu theoretisieren, wobei es immer um Zustände und Operatoren oder Wirkungen zu gehen hat, gerne auch um: intrinsische.
    ‘Zeitabhängigkeit’, was ist Zeit genau außer dem Ändern von Zustand, dessen Feststellung erkennenden Subjekten obliegt?, rundet das dbzgl. Vorhaben dann sozusagen ab.

    MFG + schönen Sonntag noch,
    Dr. W

  8. #8 MartinB
    14. Juni 2015

    @Niels
    Ja, ich hab’s bisher auch immer so geschluckt, aber ich fand es eben immer extrem unanschaulich, von einem zeitunabhängigen Zustand zu reden – entweder es ist zeitabhängig, oder es sollte nicht “Zustand” heißen, weil Zustände sich
    nun mal ändern. Aber gerade in der QFT kam ich mit der Vorstellung “Zustände sind zeitunabhängig” nie richtig klar – insbesondere, weil die Wirkung von Operatoren die Zustände ja ändert. Dank der Uminterpretation sehe ich jetzt klarer, wie das funktioniert.

    Ich denke auch nicht, dass meine Interpretation falsch sein kann, sind ja dieselben Gleichungen.

    “Oder ist das nur mein Eindruck?”
    Nein, so ging es mir auch. Aber generell ist das Physikforum (so gut die Antworten oft sind) sehr stark auf Formalismus ausgerichtet und anschauliche Erklärungen gibt es dort eher selten. Dieselbe Erfahrung habe ich mit meinen Fragen zur ART gemacht.

  9. #9 Lutz Donnerhacke
    15. Juni 2015

    Danke, Deine Erklärung ist nachvollziehbar und hilfreich.

    Das Bild “Was passiert, wenn ich die Ausgangswerte ändere?” ist ziemlich treffend. Es fokussiert den Kopf auf den wichtigen Gedanken: “Was will ich mit dem Formalismus erreichen? Wofür macht man diesen Ansatz?”

    Also herzlichen Dank dafür.

  10. #10 MartinB
    15. Juni 2015

    @Lutz
    Danke, freut mich, dass es noch jemandem hilft – ist immer ein komisches Gefühl, wenn man selbst den Eidnruck hat, eine Idee lässt einen Riesen-Knoten platzen und keine andere kann’s nachvollziehen.

  11. #11 Phero
    24. Juli 2015

    Ehrlich gesagt, verstehe ich persönlich wirklich nicht das Neue an deiner Anschauung. Genau das habe ich immer unter “eingefrorenen” Zuständen verstanden – man nehme einen Zustand (eben das Psi_0) und schiebe die gesamte Zeitahängigkeit in den Operator.
    Mir persönlich war – in der nichtrelativistischen QM – nie die Nützlichkeit des Heisenbergbildes klar. DIe Erklärung mit den verschiedenen Anfangszuständen, für die wir nur einmalig den Operator A(t) ausrechnen müssen, stimmt auch nur bedingt. Immerhin ergeben verschiedene Energie im Anfangszustand verschiedene Zeitentwicklungen. Derzeit sehe ich das Heisenbergbild eher als praktische Herleitung zum Diracbild an, welches der Intuition meiner Ansicht nach extrem zu Gute kommt.

  12. #12 MartinB
    24. Juli 2015

    @Phero
    “Ehrlich gesagt, verstehe ich persönlich wirklich nicht das Neue an deiner Anschauung.”
    Das neue ist nur, dass ich explizit sage “die fehlende Zeitabhängigkeit kommt schlicht daher, dass ich immer auf den Anfangszustand zurückrechne”; während man normalerweise sagt, dass der Zustand tatsächlich “eingefroren” ist und sich zeitlich nicht ändert. Ich sage, dass der sich schon ändern kann, dass man das nur einfach nicht anguckt, weil man eben zurückrechnet.

    “DIe Erklärung mit den verschiedenen Anfangszuständen, für die wir nur einmalig den Operator A(t) ausrechnen müssen, stimmt auch nur bedingt. Immerhin ergeben verschiedene Energie im Anfangszustand verschiedene Zeitentwicklungen.”
    Schon – aber wenn du dir z.B. mal die Original-paper von Heisenberg oder Jordan anguckst, dann wird da überhaupt nicht über die Zustände geredet, die rechnen nur mit den Operatoren.. Insofern ist das schon praktisch.