Bob merkt davon zunächst aber nichts – denn was genau Alice getan hat, kann er nicht wissen. Er sieht ja nur das Bild von oben mit dem gleichmäigen Mischmasch.
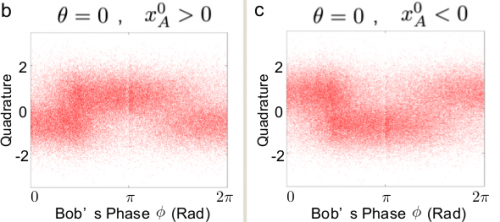
Jetzt kann Alice aber Bob sagen, wann sie den Zustand ihres “Anteils” des Photons wie beeinflusst hat, also wann sie welche Messung gemacht hat. Der Einfachheit halber beschränken wir uns auf zwei Möglichkeiten für Alices Messung, kurz mit “+” und “-” gekennzeichnet. Bob teilt jetzt seine Ergebnisse entsprechend auf, je nachdem, ob Alice ein + oder ein – gemessen hat. So sieht sein Ergebnis aus:
Die Ergebnisse von Bob und Alice sind also klar korreliert: je nachdem, was bei Alice passiert, ändern sich die Ergebnisse bei Bob. Das Photon muss also tatsächlich in irgendeiner Weise an beiden Orten zugleich sein – welche Ergebnisse die Messung bei Bob zeigt, lässt sich durch die Messung von Alice beeinflussen.
Merken kann Bob die Beeinflussung aber nur durch einen Vergleich der Ergebnisse mit Alices Messung von + oder -; ohne diesen Vergleich sieht Bob nur den Mischmasch von oben mit der gleichmäßigen Verteilung. Die Methode kann also definitiv nicht dazu verwendet werden, um Nachrichten zu schicken, weil Bob immer noch die Extra-Information über Alices Messung braucht.
Falls ihr euch übrigens die Frage stellt, wie das Experiment zur speziellen Relativitätstheorie passt (eine hinreichend schnell bewegte Beobachterin sieht ja Bobs Messung vor der von Alice) – es ist zwar im paper nicht erklärt, aber das Experiment ist in der Hinsicht letztlich symmetrisch, soweit ich sehe. Wir können genauso gut sagen, dass es Bobs Messung ist, die den Zustand des Photons festlegt und die dann die Messung von Alice beeinflusst.
Das Experiment zeigt aber noch einmal ganz klar, dass das Photon in dem Moment, wo Alice ihre Messung macht, in einem überlagerten Zustand ist. Wäre es eindeutig schon auf dem Weg zu Bob, dann könnte das, was Alice tut, ja keinen Einfluss mehr haben. Die Quantenwelt ist also wirklich ziemlich seltsam.
Fuwa, Maria, et al. “Experimental proof of nonlocal wavefunction collapse for a single particle using homodyne measurements.” Nature communications 6 (2015).






Kommentare (88)