Wenn Dinge wärmer werden, dann dehnen sie sich aus. Das ist das Prinzip hinter Flüssigkeitsthermometern, aber auch Festkörper werden größer, wenn sie wärmer werden. (Das nutzt man auch in Thermometern, beispielsweise mit Bimetall-Streifen, die sich unterschiedlich stark dehnen und deshalb verbiegen.) Versucht man zu verstehen, warum das eigentlich so ist, dann stellt man fest, dass der Effekt deutlich weniger simpel ist, als man auf den ersten Blick denken könnte.
Gase und Flüssigkeiten
Fangen wir mit der einfachsten Substanz an, die wir in der Physik haben: Einem idealen Gas. In so einem Gas haben wir Atome (oder Moleküle), die sich (wie ideale Billardkugeln) elastisch aneinander stoßen (also bei einem Stoß nicht aneinander kleben bleiben) und dabei Energie austauschen können, die aber ansonsten nicht miteinander wechselwirken.
Die Temperatur eines Gases hängt direkt an der Geschwindigkeit der Atome – je höher die Temperatur, desto schneller sind die Atome unterwegs. (Dabei sind nicht alle Atome gleich schnell, vielmehr stellt sich eine Verteilung der Geschwindigkeiten ein, die berühmte Maxwellsche Geschwindigkeitsverteilung. Diese Details können uns aber egal sein.)
So ein Gas dehnt sich zunächst mal natürlich immer weiter aus – wenn es keine Wände oder ähnliches gibt, die das Gas einsperren, dann verdünnt es sich immer weiter. Eine Wolke aus so einem Gas im Weltall würde sich immer weiter verdünnen. (Naja, nicht wirklich, weil sie ein bisschen durch die Schwerkraft zusammengehalten wird, aber die vernachlässige ich hier, es soll ja ein ideales Gas sein. Bei Gasen auf der Erde ist die gravitative Anziehung zwischen den Gasatomen auch tatsächlich winzig klein.)
Um die thermische Ausdehnung eines Gases zu sehen, müssen wir es also irgendwie einsperren. Packen wir es in einen Behälter mit festen Wänden (beispielsweise eine Flasche, die wir fest zudrehen), dann dehnt sich das Gas aber natürlich nicht aus, wenn wir es erwärmen – kann es ja nicht, die Flasche verhindert das ja.
Besser ist es, wenn wir unser Gas nicht in ein festes Volumen einschließen, sondern es stattdessen zum Beispiel in einem Ballon haben. Die Membran des Ballons übt auf das Gas einen (näherungsweise) konstanten Druck aus. Der wird dadurch von Innen ausgeglichen, dass die Gas-Atome gegen die Membran prallen und so eine Gegenkraft ausüben. Ein Atom, das von der Wand abprallt, kehrt dabei seine Geschwindigkeit und somit auch seinen Impuls (die physikalische Größe Masse mal Geschwindigkeit) um – nach dem zweiten Newtonschen Gesetz ist die Kraft die zeitliche Änderung des Impulses. Prallt das Atom von der Wand ab, übt es also eine Kraft aus und hindert so die Wand (die Gummimembran) daran, sich zusammenzuziehen.
Wenn wir jetzt die Temperatur erhöhen, erhöht sich die Geschwindigkeit der Atome. Sie prallen also zum einen stärker auf die Wand, zum anderen (weil sie ja schneller sind) auch öfter. Die Kraft, die sie ausüben, wird also größer. Entsprechend dehnt sich der Ballon aus. Durch das Ausdehnen des Ballons sind die Atome jetzt weniger dicht als vorher – das wiederum verringert die Anzahl der Atome, die zu einer bestimmten Zeit auf die Ballonwand treffen. Der Ballon dehnt sich also immer weiter aus, bis wieder ein Gleichgewicht erreicht ist. Die Atome treffen jetzt heftiger auf die Wand als bei niedriger Temperatur, aber die geringere Dichte des Gases sorgt dafür, dass die Kraft auf die Wand die selbe ist wie vorher.
Gase dehnen sich also aus, weil die Gasatome schneller werden und so bei gleicher Dichte einen größeren Druck ausüben würden. Bei Flüssigkeiten ist das ähnlich – hier ist aber die Wechselwirkung zwischen den Atomen größer, so dass die Flüssigkeit einen stärkeren Zusammenhalt hat.
Festkörper
Ganz anders sieht es aber bei festen Stoffen aus – beispielsweise einem Klotz aus Eisen. Auch im Vakuum hat der Klotz aus Eisen ein festes Volumen und verteilt sich nicht beliebig weit über das Universum. (O.k., wenn wir extrem lange warten, dann würde er das irgendwann tun, weil es eine winzige Wahrscheinlichkeit gibt, dass sich ein Atom von der Oberfläche löst, das dann im Vakuum des Weltalls in die Unendlichkeit abhauen würde. Die Zeitskala dafür ist bei einem Eisenklotz aber extrem lang.) Trotzdem dehnt sich der Eisenklotz aus, wenn wir ihn erwärmen, auch im Vakuum. Anders als beim Gas spielt also der äußere Druck für die thermische Ausdehnung keine wesentliche Rolle.
Um die thermische Ausdehnung im Eisen trotzdem zu verstehen, müssen wir uns auch hier angucken, was eine höhere Temperatur eigentlich bedeutet. Die Eisen-Atome sind in einem Stück Eisen in einem Kristallgitter angeordnet. Es gibt dabei einen energetisch besonders günstigen Abstand der Atome zueinander. Bei sehr niedriger Temperatur (wenn unser Eisenklotz den Zustand niedrigst-möglicher Energie einnimmt) haben die Eisenatome alle brav diesen Abstand, den Gleichgewichtsabstand. (Naja, ich vereinfache hier etwas: Auch bei Temperatur Null sind die Atome nicht völlig in Ruhe, das verbieten die Spielregeln der Quantenmechanik. Da ich das aber zum einen schon mal ausführlich erklärt habe und es zum anderen für die thermische Ausdehnung nicht so wichtig ist, könnt ihr den Effekt im Moment mit gutem Gewissen ignorieren – Physik ist ja immer auch die Kunst zu wissen, welche Effekte man in welcher Situation berücksichtigen muss.)
Was unsere Eisenatome auf Abstand hält, ist also die Kraft zwischen ihnen. Ihr könnt euch die ein bisschen vorstellen wie eine Feder – würde man zwei Atome dichter zusammendrücken oder weiter auseinanderziehen wollen, müsste man gegen diese Federkraft anarbeiten. Im Gleichgewichtsabstand hat die Feder genau ihre Gleichgewichtslänge, also die, bei der sie gerade keine Kraft zwischen ihren Enden ausübt.
Wenn wir jetzt die Temperatur erhöhen, dann stecken wir Energie in den Kristall. Die äußert sich darin, dass die Atome anfangen zu schwingen. Da sie ja aneinander gebunden sind, können sie nicht frei durch die Gegend sausen wie die Gasatome im Ballon. Sie schwingen also um den Gleichgewichtsabstand herum. (Ähnlich wie eine Masse, die ihr an eine Feder hängt, hin- und herschwingt, wenn ihr die Feder einmal in die Länge zieht und dann loslasst.) Im Bild haben ich die Gleichgewichtslage in blass-rot eingezeichnet und die aktuelle Lage der Atome darüber.
Wie bei Schwingungen üblich, wandeln die Atome dabei ständig potentielle Energie (also die Dehnung der Bindungen oder Federn) in kinetische Energie (also Bewegungsenergie) um: Sind bei einer Schwingung zwei Atome maximal weit auseinander, dann haben sie eine hohe potentielle Energie, kehren aber ihre Bewegung ja gerade um, so dass ihre kinetische Energie gleich Null ist, sind sie genau im Gleichgewichtsabstand, dann ist ihre potentielle Energie Null, dafür haben sie jetzt aber eine hohe Geschwindigkeit. (Das ist genau analog zum Schaukeln auf einer Schaukel – wenn ihr im untersten Punkt seid, seid ihr schnell, wenn ihr am Umkehrpunkt seid, habt ihr eine größere potentielle, aber eine verschwindende kinetische Energie, weil ihr für einen Moment in Ruhe seid.)
Unsere Atome schwingen jetzt also hin und her. (Streng genommen müsste man diese Schwingungen auch wieder mit den Mitteln der Quantenmechanik – als sogenannte “Phononen” – beschreiben, aber das spare ich mir hier.) Irgendwie muss diese Schwingung jetzt für die thermische Ausdehnung sorgen.
Um zu sehen, wie das geht (oder eben nicht geht, wartet’s ab), müssen wir beachten, dass die Atome in einem Kristall ja nicht alle im Gleichtakt schwingen – hier sind gerade zwei Atome besonders dicht, dort sind sie im Gleichgewichtsabstand, dahinten sind zwei weit auseinander. Um zu sehen, was im Kristall als Ganzes passiert, müssen wir also über alle Atome mitteln und sehen, wie sich der mittlere Abstand der Atome verhält.
Statt viele Atome zu einer Zeit zu betrachten, können wir auch umgekehrt ein Atom über einen längeren Zeitraum verfolgen. Nach den Regeln der Thermodynamik sollte dabei dasselbe herauskommen (Expertinnenhinweis: Das böse Fass “Ergodenhypothese” lassen wir mal gaaanz fest geschlossen…). Am einfachsten denken wir wieder an die Schaukel, die ist vermutlich allen aus dem Alltag vertraut. Wir schaukeln auf der Schaukel, mal doller, mal weniger doll (weil die Energie der Atome zufälligen Schwankungen unterliegt). Wenn wir unsere Position über einen langen Zeitraum mit viel Schaukelei mitteln, was wird dabei herauskommen?
Da das Vor- und das Zurückschaukeln vollkommen symmetrisch sind, ist eigentlich klar, dass sich unsere mittlere Position nicht ändern kann – wir sind genau so oft vorn wie hinten, im Mittel bleiben wir also am Ort. Genauso ist es auch in unserem Kristall, so, wie wir ihn bis jetzt betrachtet haben: Die Atome schwingen zwar hin und her, aber im Mittel ist der Abstand zwischen zwei beliebigen Atomen immer noch derselbe. Von thermischer Ausdehnung also keine Spur.
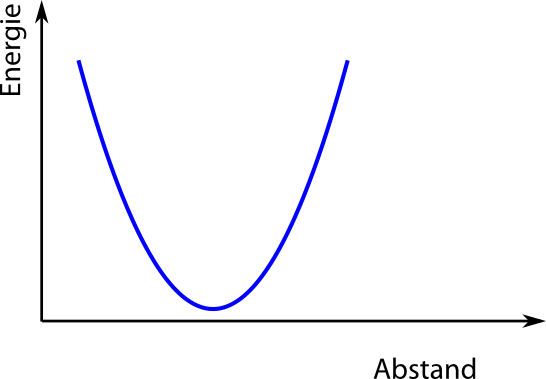
Da wir experimentell aber wissen, dass Metalle sich thermisch ausdehnen, müssen wir irgendetwas übersehen haben. Ich hab’s sogar oben schon gesagt: Der mittlere Ort ändert sich bei der Schaukel nicht, weil das Vor- und Zurückschaukeln vollkommen symmetrisch ist. Auch bei einer (idealen) Feder ist das so – auch da ist die Kraft dieselbe, wenn ich die Feder ein bisschen dehne oder sie um den selben Betrag stauche. (Ein solches Kraftgesetz nennt man auch “harmonisch” – in der Physik dient es als beliebtes Spielzeugmodell für alles mögliche, von einfachen Schwingungen bis hin zur Quantentheorie.) Wenn wir die Energie der Atome als Funktion des Abstands in diesem Modell auftragen, ergibt sich eine hübsche Parabel.
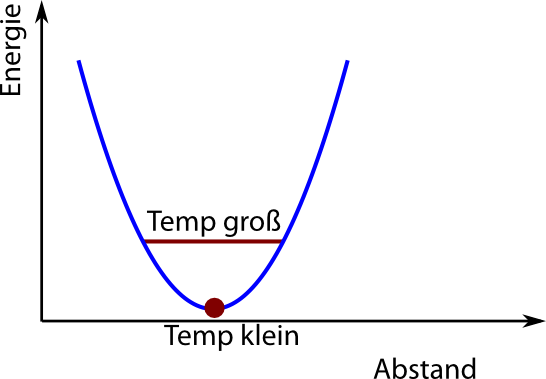
Bei niedriger Temperatur ist das System im Gleichgewicht, also ganz unten beim Zustand niedrigster Energie. Bei höherer Temperatur hat es auch eine höhere Energie, es ist deshalb mal links, mal rechts vom Gleichgewicht (ihr könnt euch vorstellen, dass es hin- und her-pendelt), aber der mittlere Abstand ändert sich nicht:
Dieses einfache Modell der Anziehung ist zwar extrem praktisch (und macht insbesondere das Berechnen vieler Dinge sehr leicht), aber es stimmt eben nicht wirklich mit der Realität überein. Die Anziehung zwischen den Eisenatomen beruht auf der Wechselwirkung ihrer Elektronen. Um die korrekt zu beschreiben, braucht man die Mittel der Quantenmechanik. Aber auch ohne ganz tief in die QM-Trickkiste zu greifen, können wir einsehen, dass die Kraft eine andere ist, wenn wir die Atome ein Stück voneinander entfernt haben als wenn wir sie einander annähern: Elektronen sind ja negativ geladen, wenn wir die Atome zu dicht zusammenquetschen, dann stoßen sich die Elektronen massiv ab. (Hinzu kommen noch quantenmechanische Effekte wie das Pauli-Prinzip.) Drücken wir die Atome extrem dicht zusammen, wird die Energie dazu extrem groß. Entfernen wir die Atome dagegen voneinander, dann nimmt die Energie nicht so schnell mit dem Abstand zu – bei sehr großer Entfernung ist die Energie auch nicht extrem groß, sonst würden sich alle Eisen-Atome im Universum ja mit gigantische Kraft anziehen.
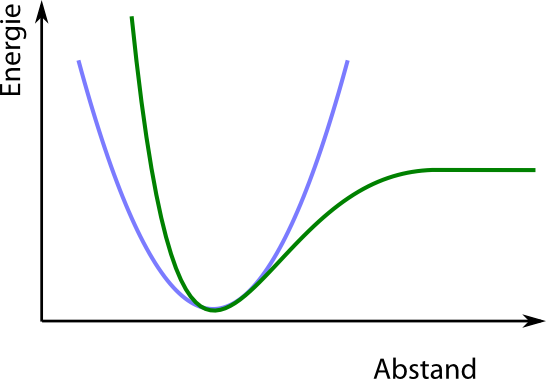
Tragen wir das wieder graphisch auf, dann sieht das Bild eher so aus (in grün die neue Energiekurve, zum Vergleich die alte symmetrische Kurve in blassblau (allerdings nicht als Frauenschrift, sondern mit inkscape generiert))
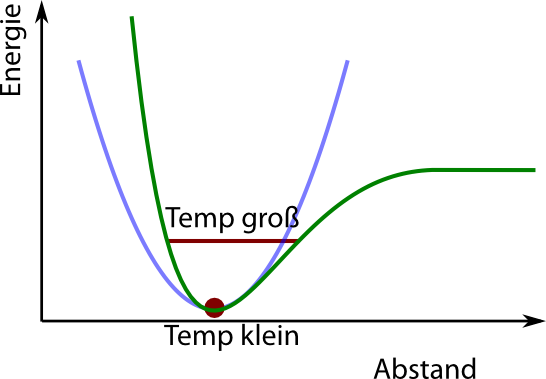
Und wenn wir jetzt den beiden Atomen etwas Energie (durch eine Temperaturerhöhung) spendieren, dann erlaubt ihnen die Extra-Energie, sich ein Stück voneinander zu entfernen, sich aber nur ein deutlich kleineres Stück aneinander anzunähern:
Wie ihr seht ist der Mittelpunkt der eingezeichneten Linie nicht mehr oberhalb der Gleichgewichtslage, sondern weiter rechts, der Abstand erhöht sich also. (Wobei ich das hier nur qualitativ angucke – quantitativ müsste man berücksichtigen, dass sich bei einer bestimmten Temperatur eine Verteilung für die Energien der Atome ergibt, so dass die Atome mal etwas höher, mal etwas tiefer sitzen. Aber das spare ich mir, es geht ja nur ums Prinzip.)
Und damit wird dann der mittlere Abstand zwischen den Atomen mit zunehmender Temperatur immer größer. Die thermische Ausdehnung kommt also daher, dass die Anziehungskraft zwischen Atomen nicht symmetrisch ist. (Vornehm ausgedrückt: Es ist ein anharmonischer Effekt, weil Schwingungen mit dem hübschen Parabel-Verlauf der Energie eben harmonisch heißen und dieser Effekt durch die Abweichung von der harmonischen Schwingung zu Stande kommt.)
Wir können die thermische Ausdehnung also nutzen, um etwas über die Anziehung zwischen den Atomen eines Materials zu lernen. Beispielsweise ist die thermische Ausdehnung von Metallen typischerweise deutlich größer als die von Keramiken (was jede Menge Ärger macht, wenn man Metalle mit Keramiken beschichtet). Das liegt daran, dass die metallische Bindung eine vergleichsweise lange Reichweite hat, während die Bindungsenergie in Keramiken mit dem Abstand sehr schnell zunimmt.
Auch wenn ich ja eigentlich eher die Theoretikerin bin – vielleicht möchte ja doch jemand auch ein paar Zahlen sehen? Die Wärmedehnung wird durch den thermischen Ausdehnungskoeffizienten beschrieben – der gibt an, um wie viel sich ein Objekt bei einer Temperaturerhöhung um ein Grad (Kelvin oder Celsius) längt. Metalle haben typischerweise Werte von so etwa 0,000 01-0,000 02/K. (Ich hoffe, ich hab mich bei den Nullen nicht verzählt.) Bauteile aus Metall werden also bei einer Temperaturerhöhung um ein Grad um 0,001-0,002% größer. Bei Keramiken sind die Werte noch etwas niedriger und liegen so bei 0,000 005/K.
Auch wenn die Werte klein sind, ist es doch wichtig, den Effekt der thermische Ausdehnung zu beachten. Bauteile, die dem deutschen Wetter ausgesetzt sind wie Brücken oder Eisenbahnschienen erleben Temperaturdifferenzen von maximal so etwa 80°C (-25°C im Winter, +55°C in der – leider zu seltenenen – knalligen Sonnenhitze). Deswegen müssen solche Bauteile entsprechende Dehnungsfugen haben oder anderweitig vor der thermischen Ausdehnung geschützt würden – Metallteile könnten sich sonst verbiegen, Bauteile aus Beton würden bei wiederholtem Schrumpfen und Längen irgendwann Risse bekommen. (Heutige Bahnschienen haben aber keine Dehnungsfugen mehr, sondern sind hinreichend fest verschweißt und auf den Bohlen verankert – Details dazu und zu anderen Alltagsbeispielen findet ihr hier.)
Deutlich extremer sind die Effekte natürlich bei Bauteilen, die richtig hohe Temperaturen erleben, wie beispielsweise Turbinenschaufeln oder auch Raketentriebwerke. Bei Temperaturschwankungen von 1000°C werden die thermischen Dehnungen so groß, dass Metalle anfangen können, sich plastisch zu verformen. Das muss man dann beim Bau solcher Dinger natürlich berücksichtigen, beispielsweise (so wie ich das tue), indem man per Simulation versucht, zu verstehen, wie genau die Spannungen sich verteilen und wie man die Bauteile vor dem versagen schützen kann.
Wenn man solche Rechnungen macht, dann muss man auch berücksichtigen, dass der thermische Ausdehnungskoeffizient selbst auch von der Temperatur abhängt. Typischerweise wird er mit zunehmender Temperatur immer größer. Das kann man mit der Energiekurve von oben auch leicht verstehen – die wird ja nach links hin immer steiler, nach rechts immer flacher – je mehr Energie ich zuführe, desto asymmetrischer ist die Kurve, desto stärker ist also die thermische Ausdehnung.
Ausnahmen
Es gibt allerdings auch Materialien, die sich mit zunehmender Temperatur nicht ausdehnen, sondern ihre Länge etwa beibehalten oder gar schrumpfen. Ein Beispiel hierfür ist (gespanntes) Gummi – das liegt an der seltsamen Kraft, die ein Gummiband zusammenschnurren lässt, die nämlich auf der Entropie beruht.
Ein anderes bekanntes Beispiel ist Eis: Wasser hat ja seine höchste Dichte im flüssigen Zustand bei 4 Grad – kühlt man es stärker ab, dann ändern sich die Bindungswinkel, so dass sich die Wassermoleküle nicht mehr ganz so dicht packen lassen. Das ist der Grund, warum Seen im Winter nicht bis zum Grund zufrieren oder warum man auf Eis Schlittschuh kaufen kann. Einen hübschen Film zum Thema findet ihr hier.(Schockwave player wird benötigt.) Auch Kohlenstoff kann diese Eigenschaft haben – in Kohlefasern ist der Ausdehnungskoeffizient in Richtung der Faser sehr klein oder sogar negativ. Das erlaubt es, Verbundwerkstoffe mit Kohlefasern herzustellen, deren thermischer Ausdehnungskoeffizient sehr klein ist, die sich also bei Temperaturerhöhung nur wenig verlängern.
Dass thermische Ausdehnung technisch auch Probleme machen kann, haben wir oben ja schon gesehen. Wenn es wirklich drauf ankommt, kann man spezielle Legierungen wie das berühmte Invar (eine Eisen-Nickel-Legierung) verwenden, die (im Raumtemperaturbereich) einen extrem kleinen thermischen Ausdehnungskoeffizienten haben. Dieser Effekt hängt mit einer magnetischen Wechselwirkung von Eisen und Nickel zusammen. Wikipedia erläutert, dass die magnetische Wechselwirkung bei niedrigen Temperaturen für eine zusätzliche Abstoßung der Atome sorgt, die dann mit zunehmender Temperatur schwächer wird. Dadurch wird dann der Gleichgewichtsabstand zwischen den Atomen kleiner, was die Zunahme des Abstands durch die Asymmetrie der Energiekurve gerade kompensieren kann.
Auch wenn uns die thermische Ausdehnung gerade von Festkörpern aus dem Alltag sehr vertraut ist – denkt man darüber nach, woher sie kommt, stellt man fest, dass es sich doch um ein ziemlich trickreiches Phänomen handelt.








Kommentare (17)