Spingitter
Tja, soweit die Turingmaschinen. Mit Physik hat das ganze aber erst mal nicht viel zu tun und es ist auf den ersten (oder zweiten oder auch zehnten) blick nicht gerade offensichtlich, dass man die Eigenschaften von physikalischen Systemen mit Turingmaschinen oder gar dem Halteproblem in Verbindung bringen kann. Und tatsächlich ist die Verbindung in der Arbeit, um die es hier geht, auch ziemlich kompliziert – ich habe zugegebenermaßen selbst nicht alles im Detail verstanden, hoffe aber, dass ich die grobe Idee einigermaßen wiedergeben kann. Falls euch die physikalischen Modelldetails nicht so interessieren, könnt ihr jederzeit auf die dritte Seite des Artikels springen, wo ich mir ein paar gedanken mache, was das Ganze eigentlich bedeutet.
Das System, mit dem wir uns beschäftigen, ist ein Spingitter. Stellt euch ein regelmäßiges zweidimensionales Gitter vor, wie beispielsweise ein Schachbrett (oder ein zweidimensionales Kristallgitter). In jedem Feld des Schachbretts sitzt ein physikalisches Objekt (so etwas wie ein Atom). Dieses Objekt kann in verschiedenen Zuständen vorliegen. Der einfachste Fall wäre, dass es zwei Zustände gibt. Quantenmechanisch kann man sich darunter zum Beispiels Spins vorstellen – also die Drehimpulse von Teilchen wie Elektronen, die in zwei Zuständen vorliegen können, meist einfach als Spin rauf und Spin runter bezeichnet. (Mehr über den Spin findet ihr hier, mehr über quantenmechanische Zustände hier.) So etwa könnte das aussehen (das zweidimensionale Feld ist hier ein bisschen perspektivisch gezeichnet):
Spingitter sind ziemlich schicke Dinger und man kann sie nutzen, um damit alle möglichen Phänomene in der Physik zu veranschaulichen. Für uns heute ist nur die Energie eines Spingitters wichtig. Nehmen wir wieder den einfachsten Fall, wo wir nur zwei Spins haben (rauf und runter). Wenn es energetisch günstig ist, wenn die Spins in benachbarten Schachbrettfeldern (oder Gitterplätzen) gleich ausgerichtet sind und energetisch ungünstig, wenn sie entgegengesetzt ausgerichtet sind, dann ist der energetisch günstigste Zustand der, wo alle Spins in dieselbe Richtung zeigen (rauf oder runter, das ist egal). Ein solches Modell ist ein Ising-Modell, man kann mit ihm zum Beispiel verstehen, wie Magnete funktionieren und warum Materialien bei hohen Temperaturen ihre ferromagnetischen Eigenschaften verlieren. Mehr über das Ising-Modell und sein Verhalten bei unterschiedlichen – und sogar negativen – Temperaturen könnt ihr hier nachlesen.
Nach den Regeln der klassischen Physik ist jeder Spin entweder “rauf” oder “runter” – die Zahl der Möglichkeiten für einen Spin ist also endlich. Das bleibt auch so, wenn wir mehr als einen Spin an jedem Punkt haben oder wenn jeder Spin mehr als eine Möglichkeit hat (beispielsweise rauf runter recht links) – in beiden Fällen brauche ich nach den Regeln der klassischen Physik nur eine natürliche Zahl, um den Spin zu beschreiben (1-rauf 2-runter usw.).
In der Quantenmechanik ist die Sache aber komplizierter. Hier können unsere Spins nicht nur einfach die beiden Zustände “rauf” und “runter” haben, sondern auch in einem Üerlagerungszustand sein, sozusagen 73,7% rauf und 26,3% runter. Um einen Quantenzustand zu kennzeichnet, genügt also nicht ein einziges Bit (0 oder 1 für rauf oder runter), sondern man braucht eine reelle Zahl. In diesem Sinn enthält ein einzelner Quantenzustand also unendlich mehr Informationen als ein klassischer Zustand. Das Problem dabei ist, dass man diese Zahl nicht direkt auslesen kann – wenn man den Zustand tatsächlich zu messen versucht, bekommt man auch in der QM immer entweder Null oder Eins als Ergebnis. Trotzdem kann man die Extra-Information ausnutzen, das ist genau das, was z.B. Quantencomputer tun oder was bei der Quantenverschränkung passiert. Details findet ihr in der Serie “Quantenmechanik verstehen” (siehe rechts bei den Artikelserien) – aber Details sind heute wie gesagt nicht so wichtig, heute geht es um das große Ganze.
Die Turing-Maschine auf dem Spin-Gitter
Als nächstes bastelt man eine Turingmaschine in unser System. Das tut man mit Hilfe der Energie, oder vornehm gesagt, des Hamilton-Operators. Der Hamilton-Operator ist in der Qm eine Rechenvorschrift, mit der ich aus dem aktuellen Zustand meines Spingitters die Energie des Spingitters berechnen kann. (Naja, das war jetzt wieder etwas vereinfacht, macht aber nix.) Im einfachen Fall des Ising-Modells von oben ist der Hamilton-Operator sehr simpel, er besagt einfach: Betrachte alle paare von nächsten Nachbarn auf dem Gitter und multipliziere die Spinwerte (die als -1 oder +1 geschrieben werden) miteinander. Summiere das auf und nimm das Negative davon. Da minus mal minus plus ist, ist das Produkt benachbarter Spins plus 1, wenn beide gleich sind, und minus 1, wenn sie ungleich sind. (Bei Überlagerungszuständen tragen dann beide Werte passend bei, aber auch das sind wieder Details…) Und weil wir am Ende noch mal das Negative nehmen, ist die Energie am niedrigsten, wenn alle Spins gleich sind.
Wie haben ja im Abschnitt über Turingmaschinen gesehen, dass es für jede Turingmaschine eine Zahl T gibt, die diese Maschine kennzeichnet. Diese Zahl T wird jetzt in die Rechenvorschrift für den Hamilton-Operator eingebaut. Dazu genügt es allerdings nicht, wenn die Spins an jedem Punkt nur zwei mögliche Werte haben – man braucht hier ein System mit deutlich höherer Dimension. Wie groß diese Dimension genau ist, wird im paper nicht vorgerechnet, entscheidend ist aber, dass man zeigen kann, dass es einen endlichen Wert d gibt, der immer ausreicht, das System wird also nicht bereits an einem Punkt unendlich komplex.
Hier verwendet man implizit die Quanteneigenschaft des Systems. Klassisch kann ich – wenn ich jeweils d Spins an jedem Ort habe – die Energie des Systems für alle denkbaren Kombinationen benachbarten Spins als Tabelle angeben – das sind dann d² Zahlen. Ich kann also nie mehr Information speichern, als ich in diesen d² Zahlen schreiben kann. In der QM ist das wegen der Überlagerungen aber anders, dort können die Wechselwirkungen beliebig kompliziert werden.
O.k., ich tue jetzt nicht mal so, als hätte ich im Detail verstanden, wie diese Codierung des Hamilton-Operators durch eine Turingmaschine funktioniert. Die Grundidee ist aber die folgende: Nehmt an, die Turingmaschine würde durch die natürliche Zahl T gekennzeichnet. T kann beliebig groß werden, was Probleme mit sich bringt, denn dann wird es schwierig, am Ende Energien zu berechnen, die eine obere Grenze haben (was aber für den Beweis notwendig ist). Man baut deshalb aus der Zahl T eine Zahl zwischen Null und eins. Dazu schreibt man T als Binärzahl. Wäre T zum Beispiel 14, dann gilt 14= 8+4+2=1 * 2³+ 1 * 2² + 1*21+0*20. Die Binärdarstellung von 14 ist also 1110. Wir kehren diese Zifernfolge jetzt um und setzen ein 0, davor, also wird aus 14 die Zahl 0,011100000…. Diese Zahl können wir jetzt als binäre Zahl zwischen Null und 1 interpretieren. Auf diese Weise kann man jede natürliche Zahl als Zahl zwischen Null und Eins schreiben. Die entsprechende neue Zahl wird also in den Hamilton-Operator eingebaut.
Eine Turing-Maschine durchläuft ja eine Reihe von Zuständen, sie hat sozusagen eine Dynamik. In unserem Quantensystem gibt es so eine Dynamik nicht, wenn wir die Energien angucken, denn es ist eine Eigenschaft von Quantensystemen, dass Zustände mit definierter Energie statisch sind, sich also mit der Zeit nicht ändern. (Abgesehen von einem für uns hier mal wieder unwichtigem Phasenfaktor – schreibe ich nur hin, damit ich nix falsches sage.) Um die gesamte Berechnungsgeschichte einer Turing-Maschine trotzdem ins Quantensystem zu bekommen, konstruiert man jetzt den Grundzustand des Systems aus einer Überlagerung von lauter Einzelzuständen, von denen jeder einen momentanen Zustand der Turingmaschine darstellt. Der Hamilton-Operator wird also gerade so konstruiert, dass er genau diesen Grundzustand hat, und zwar genau für die Berechnungsgeschichte der Turingmaschine mit der Zahl T (die wir über das Binärcodierungsverfahren in den Hamilton-Operator reinbekommen.)
Was man als Ergebnis bekommen möchte, ist ein System, das folgende Eigenschaft hat: Wenn die Turingmaschine T hält, dann hat unser System eine Energielücke – die Energie des ersten angeregten Zustandes ist um einen endlichen Betrag größer als die des Grundzustandes (und dieser Betrag ist unabhängig von der Größe unseres Spingitters). Wenn die Turingmaschine nicht hält, dann gibt es ein kontinuierliches Energiespektrum, der Grundzustand und der erste angeregte Zustand liegen also beliebig dicht beieinander.
Um diese Eigenschaft korrekt einzubauen, wird die Sache noch weiter verkompliziert. Dazu betrachtet man jetzt lokale Bereiche innerhalb des Gitters und die Zustände innerhalb dieser Bereiche. Man verwendet dazu quasi-periodische Kachelungen. Die funktionieren so, dass man nur Kacheln aneinander legen darf, deren Kanten farblich zusammenpassen. Hier ein Beispiel für solche Kacheln:
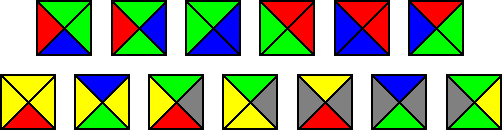
“Wang tiles“. Licensed under Public Domain via Commons.
Mit diesen Kacheln kann man jetzt versuchen, die Ebene zu überziehen. (Die Kacheln dürfen dabei nicht gedreht werden, sonst wäre es zu einfach.) Das geht, aber das Ergebnis ist nicht periodisch, es gibt also kein sich immer wieder wiederholendes Muster:

“Wang tesselation” by Claudio Rocchini – Own work. Licensed under CC BY-SA 3.0 via Commons.
Es ist bekannt, dass es nicht vorhersagbar ist, ob ein gegebener Satz solcher Kacheln in der Lage ist, die Ebene zu überziehen – das ganze ist mathematisch äquivalent zum Halteproblem.
Wir können jetzt so eine Kachelung in unser Quantensystem einbauen. Dazu ordnen wir (ich hoffe, ich habe das richtig verstanden) jeder möglichen Kachel einen Zustand der Teilchen auf unserem Spingitter zu (wenn es 13 Kacheln gibt, brauchen wir also 13 Zustände). Die Regel, dass benachbarte Kacheln immer passende Farben haben, können wir in eine Energie übersetzen: Wenn an einem Gitterplatz z. B. die Kachel oben links sitzt, die an der rechten Seite grün ist, dann bekommt die Energie einen positiven Wert, wenn die Kachel rechts daneben nicht passt (also auf der linken Seite nicht grün ist). Da der Grundzustand der Zustand mit der niedrigsten Energie ist, kann man so erzwingen, dass im Grundzustand alle Kacheln perfekt passen. (Hier habe ich ein kleines Problem, weil eine Kachelung beliebig viele Kacheltypen enthalten darf, wenn ich es richtig verstehe; für den Beweis ist es aber wichtig, dass die Zahl der Zustände an jedem Gitterpunkt eine obere Grenze hat. Ist mir nicht klar, wir das zusammenpasst.)
Am Schluss werden die beiden Bestandteile zusammengefüht – der Hamilton-Operator hat also zwei Terme, einen für die Kachelung und einen, der das Verhalten der Turing-Maschine abbildet. Und dann ergibt sich das gewünschte Resultat: Das Energiespektrum des Systems hat im Grenzfall, dass man das Gitter unendlich groß macht, genau dann eine Lücke, wenn die Turingmaschine T hält. Da das Halteproblem nicht durch einen Algorithmus entschieden werden kann, kann auch die Frage, ob ein solches physikalisches System eine Energielücke hat, nicht durch einen Algorithmus entschieden werden.






Kommentare (83)