Das Physik und Mathematik eng zusammenhängen, ist ja nichts Neues. Dass dieser Zusammenhang aber so eng sein kann, dass man Kernsätze der theoretischen Mathematik, die sich mit den Grenzen der Berechenbarkeit beschäftigen, in physikalischen Modellen wieder finden kann, das ist allerdings schon etwas Neues. Dies zu zeigen ist vor kurzem gelungen. Die zugehörige Arbeit ist in Kurzform (auf 5 Seiten) bei Nature erschienen – das paper, das den kompletten Beweis enthält, gibt es aber auch als Langfassung mit 146 Seiten. (Quellen wie immer am Ende des Artikels.)
Leider ist die Arbeit sehr komplex, abstrakt, und voller Konzepte, die ich nur vage verstehe. Eigentlich sollte mich das vom Bloggen vielleicht abhalten – auf der anderen Seite habe ich nach kurzer Googelei keine einzige einigermaßen ausführliche Erklärung dessen gefunden, was in dieser Arbeit eigentlich passiert. Also versuche ich, zumindest das, was ich so einigermaßen verstanden habe, in diesem Artikel zusammenzupacken. Korrekturen, Ergänzungen, weitere Erläuterungen usw. sind in den Kommentaren sehr gern gesehen, und wenn ihr die Arbeit komplett versteht, dürft ihr auch gern einen Gastartikel für den Blog schreiben. Seid aber auf jeden Fall gewarnt: irgendwo in diesem Blogtext steckt mit an Sicherheit grenzender Wahrscheinlichkeit ein Fehler oder eine Ungenauigkeit.
Da das ganze ziemlich abstrakt ist, bitte ich beim Lesen um etwas Geduld – bevor wir sehen, was eigentlich das physikalische Problem ist, müssen wir uns erst mal mit der den Grundlagen der Mathematik beschäftigen, genauer gesagt, mit Turing-Maschinen. Der Text hier wird also etwas länger werden, aber das ist hier auf dem Blog ja keine Seltenheit… (Aus diesem Grund habe ich auch das neue Feature des Aufteilens in mehrere Seiten verwendet – die Umbrüche sind allerdings an sinnvollen Stellen, nicht willkürlich. Auf dieser Seitegeht’s um die Mathematik und Turing-Maschinen, auf der nächsten um das physikalische Modell und falls ihr euch vor allem für die Konsequenzen interessiert, die gibt es auf der dritten Seite.)
Turing-Maschinen
Turing-Maschinen sind so etwas wie idealisierte Computer. (Achtung: Ich werde im folgenden einiges etwas vereinfachen – zum einen bin ich keine Expertin in Sachen theoretische Mathematik/Informatik, zum anderen sind die Details auch nicht soo wichtig. Und ich hoffe, es stört sich niemand, dass ich manchmal Turing-Maschine mit Bindestrich schreibe und manchmal ohne.) Sie haben einen inneren Zustand (entsprechend zu all dem, was euer Rechner gerade im RAM gespeichert hat, aber bei der Turing-Maschine ist der Zustand bloß eine einzige natürliche Zahl) und einen einfachen Papierstreifen mit Kästchen drauf, in denen entweder gar nichts, eine Null oder eine Eins steht. Ein Lese-Schreib-Kopf liest die Information auf dem Band und kann sie auch überschreiben. Die Maschine startet in einem Zustand und liest das Kästchen, auf das ihr Lese-Schreib-Kopf zeigt. Das Programm das auf der Maschine läuft, besteht aus einer Tabelle, in der für jeden gerade gelesenen Wert und für jeden möglichen Zustand der Maschine festgelegt wird, was sie als nächstes tut: Sie darf den aktuellen Wert auf dem Band überschreiben, sie darf ihren Zustand ändern und sie darf ihren Schreibkopf nach links oder rechts bewegen oder auch stehen bleiben.
Eine einfache Turingmaschine wäre also zum Beispiel MASCHINE A: Beginne im Zustand 1, schreibe eine 0 auf das Band, gehe ein Feld nach rechts, bleibe im Zustand 1. Diese Maschine würde unser ganzes Band mit Nullen vollschreiben (und weil das Band unendlich lang ist, nie fertig werden).
Ein andere Turingmaschine (MASCHINE B) wäre z.B.: Beginne im Zustand 1. Wenn du in diesem Zustand eine 1 liest, wechsle in den Zustand 2, wenn du eine Null liest, dann gehe ein Feld nach rechts. Zustand 2 ist ein Haltezustand. Das ist ein besonderer Zustand, wenn die Maschine ihn erreicht, dann bleibt sie stehe und tut nichts mehr (ihr könnt euch vorstellen, dass irgendwo ne Klingel läutet oder so, damit man das auch merkt.) Diese Maschine liest also das band und hält, wenn sie eine 1 liest – falls auf dem band keine 1 drauf ist, läuft sie immer weiter.
Die Maschine läuft also über das Band, ändert ihren inneren Zustand immer wieder, bis sie irgendwann stehen bleibt, wenn sie einen Haltezustand erreicht – oder eben nicht, wenn die Definition der Maschine keinen Haltezustand vorsieht oder der mit dem gegebenen input nicht erreicht wird (wie bei MASCHINE B, wenn ihr ihr ein band mit lauter Nullen gebt.)
Gegenüber einem realen Computer hat die Turing-Maschine einen Vor- und einen Nachteil. Der Nachteil ist offensichtlich: In so einer simplen Tabellen-Sprache ein Programm wie Matlab oder LaTeX zu schreiben, macht vermutlich wenig Spaß und dürfte ziemlich nervenaufreibend sein. Für praktische Zwecke ist eine Turing-Maschine also nicht so tauglich. Ihr Vorteil – auch gegenüber jedem real existierenden Computer – ist aber, dass das Lese-Schreib-Band unendlich lang ist (unendlich viel Speicherplatz, den könnte ich auch gut gebrauchen…). Wikipedia hat übrigens auch ein schönes Beispiel für eine solche Maschine.
Man kann jetzt eine ganz besondere Turing-Maschine konstruieren, nämlich die “Universelle Turing-Maschine”. Bisher hatte unsere Turing-Maschine ein festes Programm – die universelle Turing-Maschine dagegen kann mit beliebigen Programmen arbeiten. Dazu codieren wir die Tabelle, die angibt, was eine bestimmte Turingmaschine bei welchem Zustand und welchen Eingabedaten tun soll, als eine Abfolge von zeichen, die unsere universelle Turing-Maschine einliest. (Man kann diese Abfolge von Zeichen als eine einzige Zahl zusammenfassen, so dass jede Turingmaschine durch eine Zahl T gekennzeichnet werden kann. Dass das geht ist klar – alles,was in eurem Computer gespeichert ist, besteht aus einer Abfolge von Nullen und Einsen, die man als eine gigantische Zahl auffassen kann.) Die Maschine liest also erst ein Programm ein (das der Turing-Maschine, die wir gerade verwenden wollen) und führt dann dieses Programm aus. (Man kann die universelle Turing-Maschine der Einfachheit halber auch mit einem zweiten Band ausstatten, von dem nur gelesen werden kann und das die Programminformation enthält.) Damit ist die universelle Turing-Maschine also programmierbar und kann jede andere Turing-Maschine nachahmen.
Das Halte-Problem
Jede, die schon einmal programmiert hat, kennt das: Man bastelt irgendeine komplizierte Abfrage oder Entscheidung in das eigene Programm ein, startet es, und nichts passiert – der Rechner durchläuft eine Endlosschleife und nur ein beherztes Drücken von CTRL-C kann ihn daran hindern, dasselbe immer wieder zu tun. Auch eine Turing-Maschine kann in eine Endlos-Schleife geraten, nämlich dann, wenn sie nie einen Zustand erreicht, der als “Haltezustand” definiert wurde – dann läuft sie immer weiter und läuft und läuft und läuft. Das haben wir ja oben schon an den beiden Beispielmaschinen A und B gesehen.
Da Endlosschleifen doof sind, wäre es natürlich schick, man könnte vorher wissen, ob eine bestimmte Turingmaschine anhält oder nicht. Nehmen wir also an (ich halte mich an die Nomenklatur von Wikipedia) wir wollen wissen, ob eine Turingmaschine T (das “T” steht für die Kodierung des Programms der Maschine) in eine Endlosschleife gerät oder nicht, wen wir ihr als Start-Information ein Band mit dem Inhalt w geben (das “w” steht für die Daten, mit denen wir die Maschine füttern).
Was wir brauchen ist also ein Programm, das wir mit der Information T und w füttern und das uns dann die Antwort “Maschine hält” oder “Maschine hält nicht” gibt. Wenn wir also den Code für MASCHINE A eingeben, dann soll das programm, das wir schreiben wollen, den Code der MASCHINE A und das Eingabeband analysieren (das hier egal ist) und sagen “Maschine hält nicht”. Bei MASCHINE B müsste unser programm entsprechend den Code der Maschine analysieren, das band lesen und sagen “Maschine hält”, wenn auf dem Band eine 1 steht, und “Maschine hält nicht”, wenn keine einzige Eins auf dem Band ist.
Falls ihr jetzt denkt “ist doch einfach – ich nehme einfach die Universelle Turing-Maschine, füttere die mit T als Programm und w als Daten und schaue, ob sie anhält”, dann ist das zwar gut gedacht aber zu einfach. Denn wir wollen ja wirklich wissen, ob die Maschine anhält und nicht unendlich lange warten (weil unsere universelle Turingmaschine ja auch nicht zum Ende kommt, wenn es T nicht tut). Anders gesagt: Wir wollen ein Programm, bei dem am Ende die Info “Maschine hält nicht” herauskommen kann. Das Programm selbst (oder unsere universelle Turingmaschine) soll also auf jeden Fall einen Haltezustand erreichen, uns dabei aber die Information “T hält” bzw. “T hält nicht” geben (beispielsweise aufs band schreiben oder durch die Art des Haltezustands – es darf ja auch mehrere Haltezustände geben.)
So eine Maschine kann es aber nicht geben. Der Beweis ist ein bisschen trickreich, ich skizziere nur die Idee. (Details findet ihr bei Wikipedia oder z.B. im Klassiker “Gödel, Escher,Bach” von Hofstadter.) Er beruht darauf, dass unser Vorhersageprogramm ja selbst auch als eine Turingmaschine beschrieben werden kann. Nehmen wir an, dass wir eine Maschine H gefunden haben, die für jedes Eingabepaar (T,w) vorhersagen kann, die Maschine T hält. H liefert also eine eindeutige und richtige Antwort “hält” oder “hält nicht” für jede beliebige Turingmaschine.
Jetzt bauen wir uns eine zweite Maschine G. G verwendet das Programm von H, aber wenn H ausgibt “Maschine hält nicht”, gibt G als Ergebnis eine 1 aus. Wenn H dagegen ausgibt “Maschine hält”, dann springt G in eine Endlosschleife. Und jetzt lässt man die erste Maschine H wiederum auf G los. (Statt den Code T bekommt H also den Code der Maschine G als Eingangsdaten.) Wenn H also herausbekommt, das G hält, dann springt G in eine Endlosschleife. Wenn G in eine Endlosschleife gerät, sollte H ausgeben, dass G nicht hält, also sollte G halten. Da das offensichtlich in sich widersprüchlich ist, kann es die Maschine H nicht geben (denn wenn es sie gäbe, wäre es leicht, aus ihr die Maschine G zu konstruieren.)
Falls ihr das verwirrend findet – ist es auch. Es ist aber für das, was kommt, nicht so wichtig, dass ihr den Beweis versteht. Wichtig ist nur, dass ihr folgende Idee mitnehmt: Turingmaschinen können Berechnungen durchführen, aber es gibt Berechnungen, die auch eine Turingmaschine nicht erfolgreich durchführen kann. Nicht alles, was als mathematische Fragestellung formulierbar ist, ist berechenbar.
Achtung: Streng genommen zeigt das hier erst mal nur, dass eine universelle Turing-Maschine nicht alles berechnen kann. Bisher hat allerdings niemand etwas gefunden, das berechenbar wäre, ohne von einer Turing-Maschine berechenbar zu sein. Die berühmte Church-Turing-Hypothese sagt, dass in der Tat alles, was berechnet werden kann auch von einer Turing-Maschine berechnet werden kann – aber diese Hypothese ist nicht bewiesen und es gibt Leute (z.B. Roger Penrose), die glauben, dass quantenmechanische Prozesse vielleicht Dinge berechnen können, die einer Turing-Maschine nicht zugänglich sind. (Und Penrose verwendet das dann gleich noch, um daraus Schlüsse über unser Bewusstsein und Willensfreiheit usw. abzuleiten, die ich aber alle für vollkommen falsch halte.)
… and now for something completely different…
Spingitter
Tja, soweit die Turingmaschinen. Mit Physik hat das ganze aber erst mal nicht viel zu tun und es ist auf den ersten (oder zweiten oder auch zehnten) blick nicht gerade offensichtlich, dass man die Eigenschaften von physikalischen Systemen mit Turingmaschinen oder gar dem Halteproblem in Verbindung bringen kann. Und tatsächlich ist die Verbindung in der Arbeit, um die es hier geht, auch ziemlich kompliziert – ich habe zugegebenermaßen selbst nicht alles im Detail verstanden, hoffe aber, dass ich die grobe Idee einigermaßen wiedergeben kann. Falls euch die physikalischen Modelldetails nicht so interessieren, könnt ihr jederzeit auf die dritte Seite des Artikels springen, wo ich mir ein paar gedanken mache, was das Ganze eigentlich bedeutet.
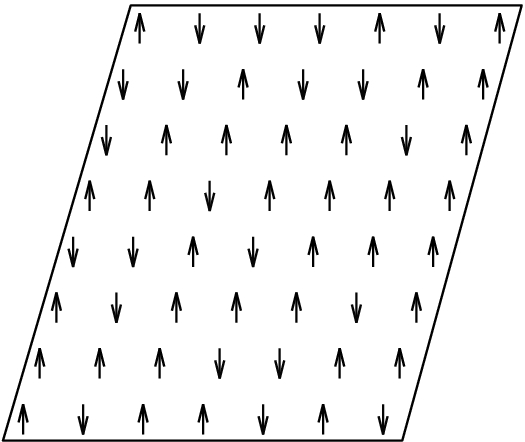
Das System, mit dem wir uns beschäftigen, ist ein Spingitter. Stellt euch ein regelmäßiges zweidimensionales Gitter vor, wie beispielsweise ein Schachbrett (oder ein zweidimensionales Kristallgitter). In jedem Feld des Schachbretts sitzt ein physikalisches Objekt (so etwas wie ein Atom). Dieses Objekt kann in verschiedenen Zuständen vorliegen. Der einfachste Fall wäre, dass es zwei Zustände gibt. Quantenmechanisch kann man sich darunter zum Beispiels Spins vorstellen – also die Drehimpulse von Teilchen wie Elektronen, die in zwei Zuständen vorliegen können, meist einfach als Spin rauf und Spin runter bezeichnet. (Mehr über den Spin findet ihr hier, mehr über quantenmechanische Zustände hier.) So etwa könnte das aussehen (das zweidimensionale Feld ist hier ein bisschen perspektivisch gezeichnet):
Spingitter sind ziemlich schicke Dinger und man kann sie nutzen, um damit alle möglichen Phänomene in der Physik zu veranschaulichen. Für uns heute ist nur die Energie eines Spingitters wichtig. Nehmen wir wieder den einfachsten Fall, wo wir nur zwei Spins haben (rauf und runter). Wenn es energetisch günstig ist, wenn die Spins in benachbarten Schachbrettfeldern (oder Gitterplätzen) gleich ausgerichtet sind und energetisch ungünstig, wenn sie entgegengesetzt ausgerichtet sind, dann ist der energetisch günstigste Zustand der, wo alle Spins in dieselbe Richtung zeigen (rauf oder runter, das ist egal). Ein solches Modell ist ein Ising-Modell, man kann mit ihm zum Beispiel verstehen, wie Magnete funktionieren und warum Materialien bei hohen Temperaturen ihre ferromagnetischen Eigenschaften verlieren. Mehr über das Ising-Modell und sein Verhalten bei unterschiedlichen – und sogar negativen – Temperaturen könnt ihr hier nachlesen.
Nach den Regeln der klassischen Physik ist jeder Spin entweder “rauf” oder “runter” – die Zahl der Möglichkeiten für einen Spin ist also endlich. Das bleibt auch so, wenn wir mehr als einen Spin an jedem Punkt haben oder wenn jeder Spin mehr als eine Möglichkeit hat (beispielsweise rauf runter recht links) – in beiden Fällen brauche ich nach den Regeln der klassischen Physik nur eine natürliche Zahl, um den Spin zu beschreiben (1-rauf 2-runter usw.).
In der Quantenmechanik ist die Sache aber komplizierter. Hier können unsere Spins nicht nur einfach die beiden Zustände “rauf” und “runter” haben, sondern auch in einem Üerlagerungszustand sein, sozusagen 73,7% rauf und 26,3% runter. Um einen Quantenzustand zu kennzeichnet, genügt also nicht ein einziges Bit (0 oder 1 für rauf oder runter), sondern man braucht eine reelle Zahl. In diesem Sinn enthält ein einzelner Quantenzustand also unendlich mehr Informationen als ein klassischer Zustand. Das Problem dabei ist, dass man diese Zahl nicht direkt auslesen kann – wenn man den Zustand tatsächlich zu messen versucht, bekommt man auch in der QM immer entweder Null oder Eins als Ergebnis. Trotzdem kann man die Extra-Information ausnutzen, das ist genau das, was z.B. Quantencomputer tun oder was bei der Quantenverschränkung passiert. Details findet ihr in der Serie “Quantenmechanik verstehen” (siehe rechts bei den Artikelserien) – aber Details sind heute wie gesagt nicht so wichtig, heute geht es um das große Ganze.
Die Turing-Maschine auf dem Spin-Gitter
Als nächstes bastelt man eine Turingmaschine in unser System. Das tut man mit Hilfe der Energie, oder vornehm gesagt, des Hamilton-Operators. Der Hamilton-Operator ist in der Qm eine Rechenvorschrift, mit der ich aus dem aktuellen Zustand meines Spingitters die Energie des Spingitters berechnen kann. (Naja, das war jetzt wieder etwas vereinfacht, macht aber nix.) Im einfachen Fall des Ising-Modells von oben ist der Hamilton-Operator sehr simpel, er besagt einfach: Betrachte alle paare von nächsten Nachbarn auf dem Gitter und multipliziere die Spinwerte (die als -1 oder +1 geschrieben werden) miteinander. Summiere das auf und nimm das Negative davon. Da minus mal minus plus ist, ist das Produkt benachbarter Spins plus 1, wenn beide gleich sind, und minus 1, wenn sie ungleich sind. (Bei Überlagerungszuständen tragen dann beide Werte passend bei, aber auch das sind wieder Details…) Und weil wir am Ende noch mal das Negative nehmen, ist die Energie am niedrigsten, wenn alle Spins gleich sind.
Wie haben ja im Abschnitt über Turingmaschinen gesehen, dass es für jede Turingmaschine eine Zahl T gibt, die diese Maschine kennzeichnet. Diese Zahl T wird jetzt in die Rechenvorschrift für den Hamilton-Operator eingebaut. Dazu genügt es allerdings nicht, wenn die Spins an jedem Punkt nur zwei mögliche Werte haben – man braucht hier ein System mit deutlich höherer Dimension. Wie groß diese Dimension genau ist, wird im paper nicht vorgerechnet, entscheidend ist aber, dass man zeigen kann, dass es einen endlichen Wert d gibt, der immer ausreicht, das System wird also nicht bereits an einem Punkt unendlich komplex.
Hier verwendet man implizit die Quanteneigenschaft des Systems. Klassisch kann ich – wenn ich jeweils d Spins an jedem Ort habe – die Energie des Systems für alle denkbaren Kombinationen benachbarten Spins als Tabelle angeben – das sind dann d² Zahlen. Ich kann also nie mehr Information speichern, als ich in diesen d² Zahlen schreiben kann. In der QM ist das wegen der Überlagerungen aber anders, dort können die Wechselwirkungen beliebig kompliziert werden.
O.k., ich tue jetzt nicht mal so, als hätte ich im Detail verstanden, wie diese Codierung des Hamilton-Operators durch eine Turingmaschine funktioniert. Die Grundidee ist aber die folgende: Nehmt an, die Turingmaschine würde durch die natürliche Zahl T gekennzeichnet. T kann beliebig groß werden, was Probleme mit sich bringt, denn dann wird es schwierig, am Ende Energien zu berechnen, die eine obere Grenze haben (was aber für den Beweis notwendig ist). Man baut deshalb aus der Zahl T eine Zahl zwischen Null und eins. Dazu schreibt man T als Binärzahl. Wäre T zum Beispiel 14, dann gilt 14= 8+4+2=1 * 2³+ 1 * 2² + 1*21+0*20. Die Binärdarstellung von 14 ist also 1110. Wir kehren diese Zifernfolge jetzt um und setzen ein 0, davor, also wird aus 14 die Zahl 0,011100000…. Diese Zahl können wir jetzt als binäre Zahl zwischen Null und 1 interpretieren. Auf diese Weise kann man jede natürliche Zahl als Zahl zwischen Null und Eins schreiben. Die entsprechende neue Zahl wird also in den Hamilton-Operator eingebaut.
Eine Turing-Maschine durchläuft ja eine Reihe von Zuständen, sie hat sozusagen eine Dynamik. In unserem Quantensystem gibt es so eine Dynamik nicht, wenn wir die Energien angucken, denn es ist eine Eigenschaft von Quantensystemen, dass Zustände mit definierter Energie statisch sind, sich also mit der Zeit nicht ändern. (Abgesehen von einem für uns hier mal wieder unwichtigem Phasenfaktor – schreibe ich nur hin, damit ich nix falsches sage.) Um die gesamte Berechnungsgeschichte einer Turing-Maschine trotzdem ins Quantensystem zu bekommen, konstruiert man jetzt den Grundzustand des Systems aus einer Überlagerung von lauter Einzelzuständen, von denen jeder einen momentanen Zustand der Turingmaschine darstellt. Der Hamilton-Operator wird also gerade so konstruiert, dass er genau diesen Grundzustand hat, und zwar genau für die Berechnungsgeschichte der Turingmaschine mit der Zahl T (die wir über das Binärcodierungsverfahren in den Hamilton-Operator reinbekommen.)
Was man als Ergebnis bekommen möchte, ist ein System, das folgende Eigenschaft hat: Wenn die Turingmaschine T hält, dann hat unser System eine Energielücke – die Energie des ersten angeregten Zustandes ist um einen endlichen Betrag größer als die des Grundzustandes (und dieser Betrag ist unabhängig von der Größe unseres Spingitters). Wenn die Turingmaschine nicht hält, dann gibt es ein kontinuierliches Energiespektrum, der Grundzustand und der erste angeregte Zustand liegen also beliebig dicht beieinander.
Um diese Eigenschaft korrekt einzubauen, wird die Sache noch weiter verkompliziert. Dazu betrachtet man jetzt lokale Bereiche innerhalb des Gitters und die Zustände innerhalb dieser Bereiche. Man verwendet dazu quasi-periodische Kachelungen. Die funktionieren so, dass man nur Kacheln aneinander legen darf, deren Kanten farblich zusammenpassen. Hier ein Beispiel für solche Kacheln:
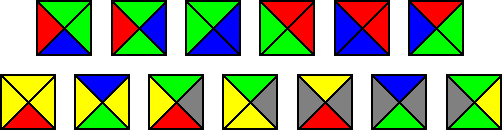
“Wang tiles“. Licensed under Public Domain via Commons.
Mit diesen Kacheln kann man jetzt versuchen, die Ebene zu überziehen. (Die Kacheln dürfen dabei nicht gedreht werden, sonst wäre es zu einfach.) Das geht, aber das Ergebnis ist nicht periodisch, es gibt also kein sich immer wieder wiederholendes Muster:

“Wang tesselation” by Claudio Rocchini – Own work. Licensed under CC BY-SA 3.0 via Commons.
Es ist bekannt, dass es nicht vorhersagbar ist, ob ein gegebener Satz solcher Kacheln in der Lage ist, die Ebene zu überziehen – das ganze ist mathematisch äquivalent zum Halteproblem.
Wir können jetzt so eine Kachelung in unser Quantensystem einbauen. Dazu ordnen wir (ich hoffe, ich habe das richtig verstanden) jeder möglichen Kachel einen Zustand der Teilchen auf unserem Spingitter zu (wenn es 13 Kacheln gibt, brauchen wir also 13 Zustände). Die Regel, dass benachbarte Kacheln immer passende Farben haben, können wir in eine Energie übersetzen: Wenn an einem Gitterplatz z. B. die Kachel oben links sitzt, die an der rechten Seite grün ist, dann bekommt die Energie einen positiven Wert, wenn die Kachel rechts daneben nicht passt (also auf der linken Seite nicht grün ist). Da der Grundzustand der Zustand mit der niedrigsten Energie ist, kann man so erzwingen, dass im Grundzustand alle Kacheln perfekt passen. (Hier habe ich ein kleines Problem, weil eine Kachelung beliebig viele Kacheltypen enthalten darf, wenn ich es richtig verstehe; für den Beweis ist es aber wichtig, dass die Zahl der Zustände an jedem Gitterpunkt eine obere Grenze hat. Ist mir nicht klar, wir das zusammenpasst.)
Am Schluss werden die beiden Bestandteile zusammengefüht – der Hamilton-Operator hat also zwei Terme, einen für die Kachelung und einen, der das Verhalten der Turing-Maschine abbildet. Und dann ergibt sich das gewünschte Resultat: Das Energiespektrum des Systems hat im Grenzfall, dass man das Gitter unendlich groß macht, genau dann eine Lücke, wenn die Turingmaschine T hält. Da das Halteproblem nicht durch einen Algorithmus entschieden werden kann, kann auch die Frage, ob ein solches physikalisches System eine Energielücke hat, nicht durch einen Algorithmus entschieden werden.
Konsequenzen
Es gibt also eine Eigenschaft eines – zumindest theoretisch denkbaren – physikalischen Systems, die durch keinen mathematischen Algorithmus entscheidbar ist. Für ein bestimmtes konkretes System kann die Frage natürlich immer noch entscheidbar sein, aber nicht für alle. Ob es solche unentscheidbaren Systeme in der Physik unseres Universums gibt, ist eine offene Frage; möglicherweise gehören Yang-Mills-Theorien, die ins Standardmodell der Elementarteilchen eingehen, in diese Klasse der unentscheidbaren Theorien, dort hat jedenfalls noch niemand die Eigenschaften des Energiespektrums berechnen können (falls ihr das in den Weihnachtsferien hinbekommt, winkt ein Preis von einer Million…)
Eine andere wichtige Konsequenz ist die folgende: Die Probleme treten auf, wenn man die Größe des Systems gegen unendlich gehen lässt. Es ist in der Physik eine oft praktizierte Technik, Dinge für immer größer werdende Systeme zu berechnen und dann in Richtung unendlich zu extrapolieren. (Beispielsweise kann man die Eigenschaften von Elementarteilchen auf immer größeren Gittern berechnen und dann am Ende extrapolieren; ähnliches macht man auch in der Festkörperphysik.) Das Ergebnis hier zeigt, dass das nicht unbedingt verlässlich möglich ist. Egal wie groß ihr ein System macht, es ist immer möglich, dass es seine Eigenschaften noch einmal fundamental ändert, wenn das System noch weiter vergrößert wird.
Es könnte tatsächlich Systeme geben, die entsprechend ihr Verhalten ändern, wenn man sie groß genug macht. Ein bisschen so, als würde Wasser zum Beispiel bei 10°C plötzlich zu Eis werden, wenn man nur hinreichen viel Wasser auf einen Haufen bringt. (Das ist jetzt nur eine Analogie, nicht das jemand das missversteht…) Solche Systeme hat man bisher nicht gefunden (man hat aber bisher wohl auch nicht nach so etwas gesucht), es ist aber durchaus möglich, dass es so etwas gibt.
Aber Achtung: Bei aller theoretischen Schönheit des Ergebnisses sollte man – das sagen sogar die Autorinnen selbst – eins im Kopf behalten:
we prove undecidabiltiy of the spectral gap …for Hamiltonians with a very particular form. We do not know how stable the results are to small deviations from this.
Wir beweisen die Unentscheidbarkeit der Energielücke für Hamilton-Operatoren mit einer sehr eigentümlichen Form. Wir wissen nicht wie stabil die Ergebnisse gegen kleine Abweichungen hiervon sind.
Wir brauchen uns nur die Konstruktion anzugucken um zu sehen, dass hier in der Tat ziemlich viel getrickst wurde: Eine Zahl wird in Binärdarstellung als reelle Zahl zwischen Null und Eins umgeschrieben. Wenn wir also eine bestimmte Turingmaschine betrachten, eren Zahl T sehr groß ist, dann muss der Hamilton-Operator auf viele Tausend oder Millionen Stellen hinter dem Komma genau die richtigen Koeffizienten haben (genau genommen sogar auf unendlich viele Stellen genau, denn wenn wir die Maschine “14” aus dem Beispiel oben als 0,0111000… kodieren, dann wäre eben 0.0111000…00100… eine ganz andere Turing-Maschine.
Auch die Konstruktion mit der Kachelung ist ja ziemlich raffiniert – auch da ist es eigentlich schwer vorstellbar, dass es reale Systeme geben soll, bei denen die Energien der Zustände genau passend zu den Farben der Kacheln sind. Ob die Resultate also tatsächlich relevant für unser Universum sind, ist nicht so klar.
Eine Frage der Unendlichkeit
Ein anderer Aspekt, der mir hierzu einfiel, der jedoch in den Artikeln nicht zur Sprache kommt, ist die allgemeine Frage nach der Rolle der Mathematik in der Physik. (Achtung: alles was ab jetzt kommt, ist auf meinen Mist gewachsen, es mag also längst geklärt, widerlegt oder anderweitig Blödsinn sein.) Es gibt ja zum Beispiel die “Tegmark-Hypothese“, die in etwa besagt “Alles was mathematisch möglich ist, existiert auch als physikalische Realität”. Dass die Mathematik unentscheidbare Aussagen enthält, ist ja seit Gödel bekannt, aber Tegmark hat bisher – laut Wikipedia – gesagt, dass es ja denkbar ist, dass nur solche Systeme auch existieren, die entscheidbar sind.
Wenn aber selbst ein Spingitter im Allgemeinen unentscheidbare Eigenschaften hat, erscheint das zumindest mir problematisch – das Grundprinzip eines Spingitters ist ja vergleichsweise einfach. Es sollte also prinzipiell Universen geben, die aus Spingittern bestehen. Wenn es aber nur solche Spingitter-Universen geben kann, die entscheidbar sind (und nicht die komplizierte Konstruktion hier), dann braucht die Natur einen Mechanismus, der entscheiden kann, ob ein bestimmtes Spingitter physikalisch realisiert werden darf (weil es einfach genug ist) oder nicht. Tja, aber diese Frage ist natürlich selbst wieder unentscheidbar, wenn ich es richtig sehe. Insofern scheint mir die Tegmark-Hypothese im Licht dieser Ergebnisse schon problematisch. (Ich bin allerdings voreingenommen, weil ich die Hypothese noch nie machte…)
Und auch wenn man sich fragt, wie zum Geier es eigentlich die Natur selbst schafft, dass sich alles an die naturgesetze hält, wird’s in meinen Augen knifflig. Klar, die Naturgesetze stehen nicht irgendwo hingeschrieben und jedes Elektron löst mal schnell die Schrödingergleichung, um zu sehen, was es als nächstes tun darf. Aber da wir die Natur ziemlich gut mit Mathematik beschreiben könne, sollte ja irgendwas an der Natur mathematisch sein (siehe auch den oben verlinkten Artikel). Wenn aber physikalische Systeme mathematisch unentscheidbar sein können, dann wird es in meinen Augen noch schwieriger sich vorzustellen, wie das eigentlich gehen soll und wie die Natur denn nun wirklich funktioniert. (Achtung – das ist natürlich keine physikalische, sondern eine metaphysische Frage. Die Physik hat nur die Aufgabem die Natur korrekt zu beschreiben und korrekte Vorhersagen zu machen, die Frage, wie die Objekte physikalischer Theorien mit den “Dingen an sich” zusammenpassen, ist keine physikalische Fragestellung. Macht sie aber ja nicht uninteressant…)
Allerdings gibt es – soweit ich sehe – einen Ausweg. Die Probleme mit Gödel und Turing und auch hier in unserem Spingitter-System handeln wir uns alle ein, weil wir beliebige Turingmaschinen (oder beim Gödel-Theorem beliebig große Zahlen) zulassen. Unser Spingitter entfaltet seine Unberechenbarkeit erst im Grenzfall eines unendlich großen Systems, und auch bei der Konstruktion der Binärzahl aus der zugehörigen Zahl T der Turingmaschine haben wir eben gesehen, dass wir hier letztlich unendlich große Präzision brauchen.
Unendlichkeiten gibt es in der Physik natürlich überall – nicht nur bei Systemen, die unendlich groß sind, sondern auch anderswo. Wir beschreiben physikalische Größen mit reellen Zahlen, ungeachtet der Tatsache das bereits eine einzige reelle Zahl unendlich viel Informationen enthält. Meist macht man sich darüber nicht so viele Gedanken, aber so richtig intuitiv ist schon das nicht. Auch anderswo in der klassischen Physik wird man schnell mit Unendlichkeiten konfrontiert, selbst wenn man nur endlich viele Objekte in einem begrenzten Raumbereich betrachtet.
Und wenn man dann zu Quantensystemen übergeht, wird es natürlich noch viel schlimmer. Wir haben das ja oben schon am Beispiel des Spins gesehen – da wo in der klassischen Physik eine einzige Zahl (0 oder 1) genügt, brauchen wir in der Qm eine reelle Zahl, also letztlich unendlich viel Information.
Dass wir selbst mit Unendlichkeiten so unsere Schwierigkeiten haben, wusste schon Kant (1. Antinomie der reinen Vernunft). Wenn aber unsere mathematische Beschreibung der Natur korrekt ist, dann sollte auch die Natur selbst Schwierigkeiten bekommen- wie unser Spingitter zeigt, kann man mit Unendlichkeiten unentscheidbare Theorien aufstellen.
Letztlich stellt sich also die Frage, ob physikalische Größen wirklich unendlich sein können (nicht unbedingt unendlich groß, sondern auch unendlich präzise, wie eine reelle Zahl). Ist es vielleicht denkbar, dass wir alle unsere physikalischen Theorien letztlich auf das Wirken endlich vieler Objekte (die auch Raum und Zeit beinhalten müssten) zurückführen können, von denen jedes nur in endlich vielen Zuständen existieren kann? Die Zahl dieser Objekte und Zustände müsste natürlich gigantisch sein, damit wir trotzdem unsere kontinuierlich aussehende Welt herausbekommen können. Und es dürfte hier keine einzige reelle Zahl geben, denn die kann bereits beliebig viel Informationen speichern.
Tatsächlich hat es solche Ideen schon gegeben. Einen Überblick findet ihr auf den sehr guten Seiten in Stanford, auch RogerPenrose diskutiert die Idee kurz in seinem Buch “Road to Reality” und zitiert dabei Arbeiten von Ahmavaara. (Ich diskutiere das jetzt nicht im Detail – dieser Post ist eh schon zu lang. Vielleicht ein andermal.) Auch wenn eine solche “endliche Physik” also ungewohnt scheint – vollkommen ausgeschlossen ist es wohl nicht, dass unser Universum letztlich so funktioniert.
Ob uns das wirklich zufrieden stellen würde, weiß ich allerdings nicht. Nehmen wir an, am Ende kommt heraus, dass die gesamte Physik sich beschreiben lässt, wenn man N Objekte betrachtet, die jeweils in M Zuständen existieren können. Wahrscheinlich würden wir sofort fragen, warum nicht “N+1” oder “M+5”? Wäre das nicht mehr logisch konsistent? Könnte es Universen mit beliebig großen Werten von N und M geben? Aber dann laufen wir gleich wieder Gefahr, in die Turing-Falle zu tappen, denn dann könnte man vermutlich wieder Universen (oder Sequenzen von Universen) finden, die ein Halteproblem codieren.
So oder so – unser Turing-Quanten-Gitter macht deutlich, wie eng Mathematik und Physik verwoben sind; selbst die Probleme der Mathematik lassen sich in physikalischen Systemen wiederfinden.
Das extrem kurze Nature-paper ist
Cubitt, Toby S., David Perez-Garcia, and Michael M. Wolf. “Undecidability of the spectral gap.” Nature 528.7581 (2015): 207-211.
Die langfassung findet ihr bei ArXiV: Undecidability of the Spectral Gap (full version)
Eine kurze Erläuterung gibt es bei nature news, die geht allerdings nicht auf das Modell im Detail ein.
Ein paar Erläuterungen gibt es auch im Blog von Scott Aaronson.






Kommentare (83)