Dann kommt Abschnitt 2 Observation (Beobachtung). Hier das 840000-Euro-Bild (soviel gibt’s für den Nobelpreis – allerdings wohl nicht dieses Jahr, wenn dieser Artikel stimmt) – zum Vergrößern anklicken, falls ihr die Veröffentlichung nicht eh aufgeklappt habt:
Quelle: LIGO, s.u.
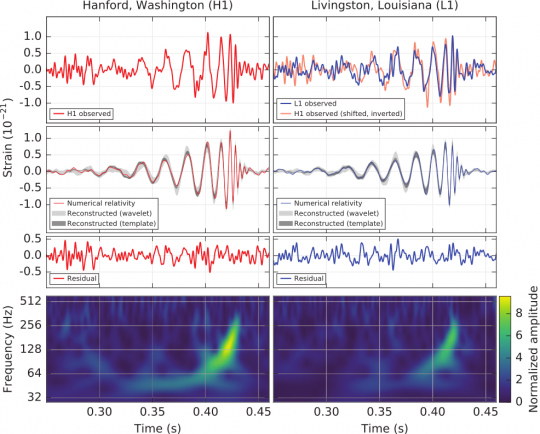
Wie sich das für Bilder in Veröffentlichungen gehört, ist hier ne Menge Information zu sehen. Die linke Spalte bezieht sich dabei auf den Detektor in Hanford, die Rechte auf den in Livingston.
In der oberen Spalte links (rote Kurve) sehr ihr das Signal in Hanford. Aufgetragen ist die Dehnung (hatte ich ja oben erklärt) gegen die zeit. (Zeitskala ist unten im Bild, der Nullpunkt der Zeitskala liegt bei 9:50:45Uhr am 14.9.2015). Ihr seht, wie die rote Linie erst mal so ein wenig vor sich hinzackelt, aber dann wird ein deutliches Wellensignal sichtbar. Die Wellen werden immer kürzer, dann klingt das Signal ziemlich schlagartig ab.
Rechts daneben seht ihr das Signal in Livingston (blau), dabei ist das Signal aus hanford (rot) überlagert. Das hanford-Signal wurde etwas zeitverzögert, weil die Signale insgesamt um knapp 7 Millisekungen auseinanderlagen (GW laufen ja mit Lichtgeschwindigkeit, aus der Verzögerung zwischen den Signalen kann man dann rückschließen, unter welchem Winkel das Signal relativ zu den Detektoren kam). Das hanford-Signal wurde dabei auf den Kopf gestellt, weil die Detektoren räumlich andersherum angeordnet sind.
In der Zeile darunter seht ihr das Ergebnis einer numerischen Simulation, die zu den Messergebnissen passt, wobei die beiden grauen Bänder unterschiedliche Annahmen machen, wie genau die Wellen mathematisch beschrieben werden. (Dazu gibt es anscheinend zwei Extra-Veröffentlichungen, da schaue ich jetzt aber erstmal nicht rein.) Nachtrag: sax hat in den Kommentaren erklärt, wie die Kurven genau zu verstehen sind, ich hatte das nicht ganz korrekt gelesen. Es wurde auf zwei unterschiedliche Weisen (mit unterschiedlichen mathematischen Ansätzen) versucht, das gemessene Signal als Welle darzustellen. Die grauen kurven geben die Streubänder an, die rote in der Mitte die beste Rekonstruktion aus den Simulationen (ich hoffe, das habe ich jetzt richtig verstanden). Darunter seht ihr, was von den ursprünglichen Kurven übrig bleibt, wenn man die rote Kurve Messergebnis abzieht. Im wesentlichen einfach Rauschen, was dafür spricht, dass das abgezogene Signal gut zur Beobachtung passt. Es wird also versucht, das gemessene Signal mathematisch sauber zu beschreiben.
Ganz unten sieht man, wie sich die Frequenz ändert. Die Frequenz ist auf der senkrechte Achse aufgetragen, die Farbe sagt, die stark der Anteil der Frequenz ist. Ihr seht z.B. links, dass das Maximum (hellgrün) erst so bei etwa 50 HZ liegt und dann schlagartig ansteigt.
Im Text dazu wird das Bild nicht weiter erläutert. (Eigentlich sollte man das nicht tun – normalerweise gehören Bilder immer auch im Text erklärt, aber vermutlich wollte man das paper nicht zu lang werden lassen.) Stattdessen wird erzählt, dass leider andere Detektoren gerade nicht in Betrieb waren, so dass man nur diese beiden hat und deshalb wenig über den Ursprung des Signals sagen kann.
Anschließend werden die Zahlen auseinandergenommen. Es gibt eine theoretische Formel für das ineinanderstürzen von SL. Die sieht so aus (nicht erschrecken):
Was sagt uns das? Links stehen die Massen der beiden Schwarzen Löcher (m1 und m2), die verschmelzen sollen. Auf der rechten Seite steht c – die Lichtgeschwindigkeit, und G, die Gravitationskonstante, sowie ein paar Zahlen (wie etwa π=3.1415926…) Dan gibt es noch f und das f mit dem Punkt drüber. f ist die Frequenz, das f mit dem Punkt drüber ist die Änderung der Frequenz. Was uns die Gleichugn sagt ist, dass wir, wenn wir die Frequenz und ihre Änderung kennen, etwas über die Massen der SL aussagen können. Wir haben nur eine Gleichung, also können wir nicht beide Massen bestimmen, aber wenn wir eine kennen, können wir die andere berechnen.
Aber immerhin – wir können den Wert ganz rechts ausrechnen, der ist etwa 30 Sonnenmassen.
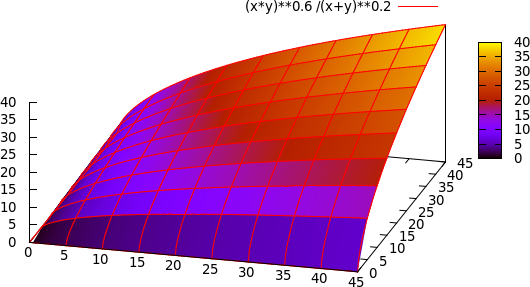
Dann kann man (ist in dem paper nicht gemacht, aber ich mache es mal) die Funktion der beiden Massen plotten, die sieht so aus:
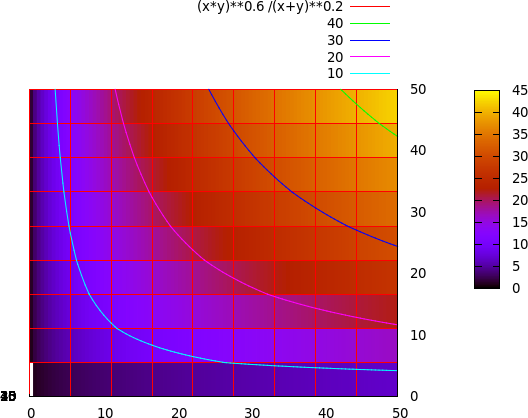
Hier nochmal eine Darstellung mit Konturlinien von oben raufgeschaut (quasi wie Höhenlinien beim Bergsteigen):
Hier kann man jetzt in Höhe der Linie bei 30 schauen, welche Massen überhaupt möglich sind. Die Gesamtmasse der beiden Objekte muss so etwa 70 Sonnenmassen betragen (gerechnet im Bezugssystem des Detektors, rückgerechnet auf das System der SL selbst wird die Masse etwas kleiner). Außerdem müssen sie sich sehr eng umkreisen, damit es die hohe Frequenz geben kann. Das schließt aus, dass es sich z.B. um Neutronensterne handeln könnte – die können so schwer nicht werden (sie haben Massen von maximal etwa 3 Sonnenmassen). Ein Paar aus einem Neutronenstern mit kleiner und einem SL mit großer Masse passt auch nicht, dann müsste das SL extrem schwer sein und der Neutronenstern würde zu langsam hineinstürzen. (Wenn ihr im Bild eine Masse groß macht, wird die andere ja klein, damit ihr auf Höhe 30 bleiben könnt.) Also muss es sich um zwei Schwarze Löcher handeln.
Für die zwei Sl spricht auch, dass das Signal sehr schnell abklingt (hatte ich ja oben schon erklärt).
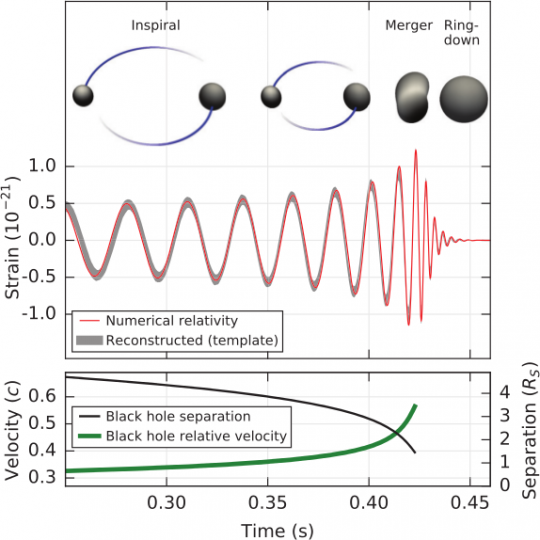
Hier das Ergebnis der besten Simulation für die beobachteten Parameter (die Kurve ist ja schon in das Bild oben eingeflossen, die grauen Streubänder geben die Messergebnisse wieder, die roten Kurven das aus dem Modell berechnete Signal ) :
Quelle: LIGO, s.u.
Oben seht ihr (neben einer Zeichnung, wie die SL sich umkreisen) die berechnete Dehnung (kennen wir schon), darunter ist die Geschwindigkeit der SL (in Einheiten der Lichtgeschwindigkeit) sowie ihr Abstand (in Schwarzschildradien, also dem Durchmesser des entstehenden SL) angegeben. (Der Radius beträgt so etwa 210 Kilometer.) Ihr seht, dass die beiden SLs am Ende rasend schnell umeinanderkreisen und dann verschmelzen.

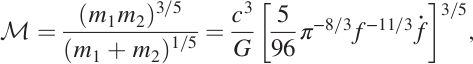





Kommentare (144)