Die maximale Eigenzeit
Wenn ihr euch nochmal an die Bewegung auf der Kugel erinnert, dann gab es dort zwei Möglichkeiten, um eine kräftefreie Bahn (also die Bewegung auf einem Großkreis) zu charakterisieren: Ihr könnt die kürzeste Verbindung zwischen zwei Punkten betrachten, oder ihr könnt an einem Ort in einer bestimmten Richtung losmarschieren. Beide Möglichkeiten legen eine Geodäte auf der Kugel eindeutig fest. (Mathematisch liegt das daran, dass ihr es mit einer Differentialgleichung 2. Ordnung zu tun habt, die braucht zwei Randbedingungen.)
Bei einer Bewegung in der Raumzeit der ART gilt dasselbe Prinzip. Eben haben wir die Bewegungsgleichung verwendet – die beruht darauf, dass ihr wisst, wann und wo ihr startet und welche Geschwindigkeit ihr habt. Dann könnt ihr zu jedem Zeitpunkt die Beschleunigung ausrechnen und damit die Bahn verfolgen.
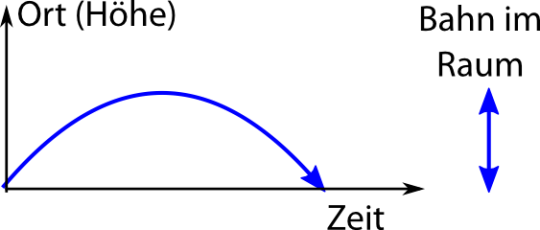
Alternativ könnt ihr euch aber auch fragen: “Welche Geodäte verbindet zwei unterschiedliche Raumzeitpunkte?” Also, in etwas alltäglicherer Sprache ausgedrückt: Welche Bahn muss ein Objekt nehmen, auf das nur die Schwerkraft wirkt, um vom Ort A in einer bestimmten zeit zum Ort B zu kommen. Wenn ihr nochmal oben auf das Bild der Parabeln schaut, seht ihr, dass die Bahn, die der nach oben geworfene Ball nimmt, eindeutig festliegt, wenn ihr wisst, wie lange der Abstand zwischen Hochwerfen und Auffangen sein soll.
Diese Geodäte lässt sich auf folgende Weise festlegen: Stellt euch vor, der Ball hätte eine kleine Uhr bei sich. Während er sich im “Schwerefeld” (also der gekrümmten Raumzeit) herumbewegt, wird der Gang dieser Uhr auf zwei Weisen beeinflusst: Zum einen dadurch, dass die Zeit ja in unterschiedlicher Höhe unterschiedlich schnell läuft, zum anderen dadurch, dass für ein schnell bewegtes Objekt die Zeit ja nach der speziellen Relativitätstheorie etwas langsamer läuft. Insgesamt ist die Geodäte diejenige Bahn in der Raumzeit, bei der die Zeit, die für den Ball vergeht, maximiert wird. (Und man kann mathematisch zeigen, dass das äquivalent zur Bewegungsgleichung ist, die wir oben aufgestellt haben, ähnlichwie die Geodäte auf der Kugel einerseits die kürzeste Verbindung zwischen zwei Punkten ist und andererseits die Kurve, der ein Objekt folgt, dass an einem bestimmten Ort in eine bestimmte Richtung losrollt.) Das ist das “Prinzip der maximalen Eigenzeit”, das ich etwas ausführlicher auch hier erklärt habe.
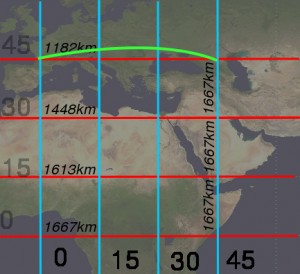
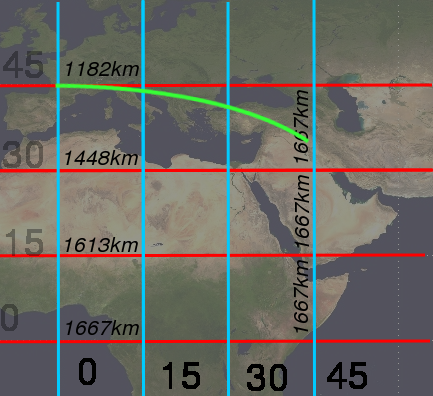
Vergleicht noch einmal die beiden Bilder der Geodäten auf der Kugel und in der Raumzeit:
Die Bahn im Bild links ist nach oben gekrümmt, weil dort die Abstände in Ost-West-Richtung zwischen den Längegraden kleiner werden, dafür müssen wir einen kleinen Nord-Süd-Umweg in Kauf nehmen. Zu weit nach oben gekrümmt darf die Bahn deshalb nicht sein, sonst wird der Nord-Süd-Umweg zu groß. Die Bahn rechts ist gekrümmt, weil in größerer Höhe die Zeit etwas schneller verläuft (und der hochgeworfene Ball soll ja die maximale Eigenzeit bekommen). Zu weit nach oben kann der Ball aber nicht fliegen, dann wird seine Geschwindigkeit zu groß (er soll ja nach festgelegter Zeit wieder ankommen), und die Zeitdilatation der SRT schlägt zu. Die Logik ist also in beiden Fällen ziemlich ähnlich.
Objekte, auf die in der ART keine Kräfte wirken (die sich also in der gekrümmten Raumzeit bewegen) folgen also Bahnen, auf denen die Eigenzeit maximiert wird. So zumindest wird es gern formuliert, die Formulierung ist so aber etwas unsauber, wie man leicht merkt, wenn man sich folgende Frage stellt: “Warum fallen Objekte eigentlich nicht nach oben?”
Klingt verrückt? Objekte sollten doch wohl nach unten fallen. Aber wenn ihr euch vorstellt, das ein Objekt seine Geodäte so “sucht”, dass es seine Eigenzeit maximiert, dann wäre es doch sinnvoll, statt nach unten nach oben zu fallen, denn oben geht die Zeit schneller und ich bekomme “mehr” Eigenzeit. Wenn man so argumentiert, vergisst man aber, dass das Prinzip der maximalen Eigenzeit in dieser einfachen Form nur angewandt werden darf, wenn ich Anfangs- und Endpunkt festlege.
Gehen wir nochmal kurz zurück zur Kugeloberfläche: Wenn ihr zwei einigermaßen dicht benachbarte Punkte auf der Kugeloberfläche (wie immer auf der Nordhalbkugel) betrachtet und euch fragt “was ist der kürzeste Weg zwischen beiden”, dann ist dieser Weg immer leicht in Richtung Norden gekrümmt. Wenn ihr analog zwei benachbarte Raumzeitpunkte betrachtet und euch fragt “was ist der Weg maximaler Eigenzeit zwischen den beiden”, dann ist die Geodäte immer nach oben gekrümmt. Wenn ihr deshalb auf der Kugel genau in Richtung Osten startet, dann bewegt ihr euch entsprechend zwangsläufig nach einer Weile nach Süden, das Bild dazu gab’s oben schon:
Um beim Weg nach Osten nach einer Weile wieder auf gleicher Höhe zu sein, müsst ihr am Anfang etwas nach Norden fliegen.
Und genauso gilt, wenn ihr in einem Schwerefeld in der gekrümmten Raumzeit im Raum-Zeit-Diagramm in horizontaler Richtung startet (ihr habt also keine Geschwindigkeit und seid anfänglich in Ruhe), dann bewegt ihr euch zwangsläufig nach unten:
Um nach kurzer Zeit wieder auf gleicher Höhe zu sein, müsst ihr am Anfang entsprechend nach oben fliegen.
Und genau deswegen fallen Dinge nach unten und nicht nach oben, auch wenn das Prinzip der maximalen Eigenzeit etwas anderes zu suggerieren scheint.
Fazit
Wie üblich ist der Artikel viiieeel länger geworden als gedacht – dass gleich drei Teile einer Serie draus werden, hatte ich am Anfang wirklich nicht erwartet. Am Ende zeigt sich aber, dass man in der ART tatsächlich (wenn man hinreichend viele Effekte vernachlässigt) die Bewegung genau so herausbekommt, wie sie auch bei Newton stand. Entscheidend dabei ist, dass die zeit in größerem Abstand von einer Masse etwas schneller verläuft. Das führt dazu, dass Geodäten “nach oben” gekrümmt sind. Die Bewegungsgleichung, die am Ende herauskommt, ist in beiden Fällen dieselbe. Bei Newton sind es Kräfte, die Beschleunigungen verursachen, in der ART ist es die Krümmung der Raumzeit (ganz analog zur Krümmung der Kugel, die unsere Geodäten auf der Landkarte krümmt). Die Verbindung zwischen beiden kommt dadurch zu Stande, dass in der Formel für die Zeitdilatation derselbe mathematische Ausdruck drinsteckt wie in der Newtonschen Formel für das Gravitationspotential.







Kommentare (17)