Nächstes Wochenende ist es wieder soweit: Das Finale der Snooker-WM beginnt am Sonntag (es endet am Montag, geht über 4 Sessions und insgesamt maximal 35 “Frames” – das Snookeräquivalent zu den Sätzen beim Tennis). Traditionellerweise laden deswegen am Wochenende die deutschen Billardvereine zum Tag der offenen Tür ein (inzwischen nehmen auch die Poolerinnen dran teil, obwohl das nun wirklich ein Sport ist, der keinen interessiert (hmm, jetzt darf ich mich vermutlich mal wieder im Verein auf ein paar böse Kommentare gefasst machen)). Ebenso traditionellerweise weise ich hier im Blog auf diese Veranstaltung hin und verbinde das mit ein paar Worten zu meinem Lieblingsspiel. Die Regeln habe ich schon erklärt, die Physik hinter verschiedenen Stößen auch schon, die Unterschiede zwischen Pool und Snooker habe ich auch schon erklärt, und letztes Jahr habe ich mir Gedanken über Statistiken und den “Fluch des Crucible” gemacht (der hat wieder gewirkt, denn Stuart Bingham ist bereits ausgeschieden). So langsam wird’s eng mit den Dingen, über die ich hier sinnvoll schreiben kann, aber nach etwas nachdenken fiel mir dann doch etwas ein, worüber ich noch nie im Detail nachgedacht habe.
Dass Snooker ein Präzisionssport ist, ist ja vermutlich allen, die sich damit beschäftigen, bekannt. Rolf Kalb weist ja gern auf die erforderliche Millimeter-Präzision hin, Mike Hallett (von der BBC) sagte mal den klugen Satz “that was a millimeter away from being inch-perfect” (merkte dann aber selbst, dass da was nicht passte).
Wie genau muss man denn nun sein beim Snooker?
Nehmen wir an, wir wollen eine Kugel lochen, die in der Mitte des Tisches auf dem blauen Spot liegt, und zwar in eine Ecktasche:

By Maciej Jaros (commons: Nux, wiki-pl: Nux) – Own work (based on Pumbaa’s version), CC BY 2.5, Link
Die Kugel hat einen Durchmesser von 52,5 Millimeter. Wäre die Taschenöffnung (der Einlauf) auch exakt so breit, dann müsste man ihn ohne jeden Fehler treffen; tatsächlich ist der Tascheneinlauf aber etwas breiter. Leider habe ich bei einer kurzen Google-Suche keine exakten Maße für die breite einer Tasche gefunden, aber bei yahoo steht “etwa 90mm”, das würde bedeuten, dass man auf jeder Seite der Kugel etwas weniger als einen halben Kugeldurchmesser an Spielraum zur Verfügung hat. Das passt zu diesem Bild hier, also nehme ich das mal als Zahl so hin.
Wenn wir die zu lochende Kugel genau auf die Mitte zielen (real würde man wohl eine Winzigkeit mehr auf die kurze Bande zielen, weil dann der Winkel etwas günstiger ist, falls man auf die Rundung der Tasche trifft, damit die Kugel trotzdem reingeht), dann haben wir einen Spielraum von (90-52,5)/2=18,75 Millimeter auf jeder Seite. Vom blauen Spot in der Tischmitte bis zur Ecke sind es 2 Meter (der Tisch ist 3569 mm x 1778 mm groß, mit dem Satz des Pythagoras ist die Diagonale über den Tisch also die Wurzel aus 3569²+1778², das ist ziemlich genau 4 Meter). Die erforderliche Präzision beträgt also plus-minus 1%.
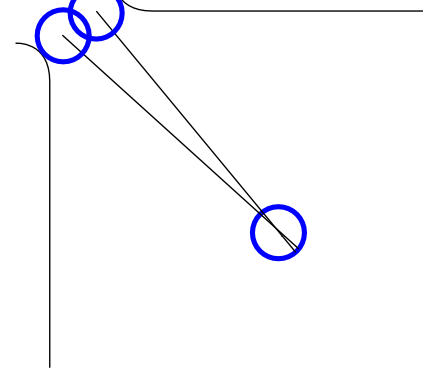
Da wir die blaue Kugel mit der Weißen anspielen, treffen sich die beiden Kugeln in genau einem Punkt. Diese Skizze (nicht maßstabsgetreu) zeigt, wie genau wir die Blaue Kugel treffen müssen:
Man sieht, dass die Linien durch den Radius der Kugel durchgehen (dort ist der Schwerpunkt der Kugel) – wenn sie am langen Ende um maximal +/-1% der Entfernung auseinanderliegen dürfen, dann auch am kurzen Ende. Dort ist die maßgebliche Entfernung der Radius der Kugel, der ja 26.25 Millimeter beträgt. Die Abweichung beim Treffen der blauen Kugel darf also nach dieser Rechnung nur +/-0,26 Millimeter betragen, das ist schon ziemlich präzise – wir müssen auf einen halben Millimeter genau treffen. (Zumindest näherungsweise deckt sich das mit den Zahlen, die diese google-Suche zu Tage gefördert hat.)
Ziemlich heftig, oder? (Wahrscheinlich werde ich in Zukunft nichts mehr treffen, seit ich diese Zahlen kenne…)
Aber wir müssen die Blaue Kugel ja auch noch mit der weißen Kugel treffen. Die weiße Kugel muss also auf weniger als einen Millimeter genau auf die blaue Kugel treffen. Man könnte jetzt versucht sein, dieselbe Rechnung zu wiederholen: Nehmen wir an, die weiße Kugel ist einen Meter entfernt, dann brauchen wir eine Präzision von weniger als einem Promille, das heißt wir müssen die weiße Kugel mit unserem Queue auf 0,026Millimeter genau treffen. Das ist aber natürlich Unsinn, so genau kann man nicht mal gucken.






Kommentare (7)