Ja, die Serie über die Gleichungen der Physik hatte ich eine Weile auf Eis gelegt – zum einen hatte ich in letzter Zeit wenig Zeit zum Bloggen, zum anderen haben mich auch andere Dinge beschäftigt, wie die Quantum Moves oder die Allgemeine Relativitätstheorie. Aber heute geht es mit der Serie weiter (die anderen Teile findet ihr, wenn ihr rechts bei den Artikelserien klickt, die Teile, die im Text hier relevant sind, habe ich auch verlinkt).
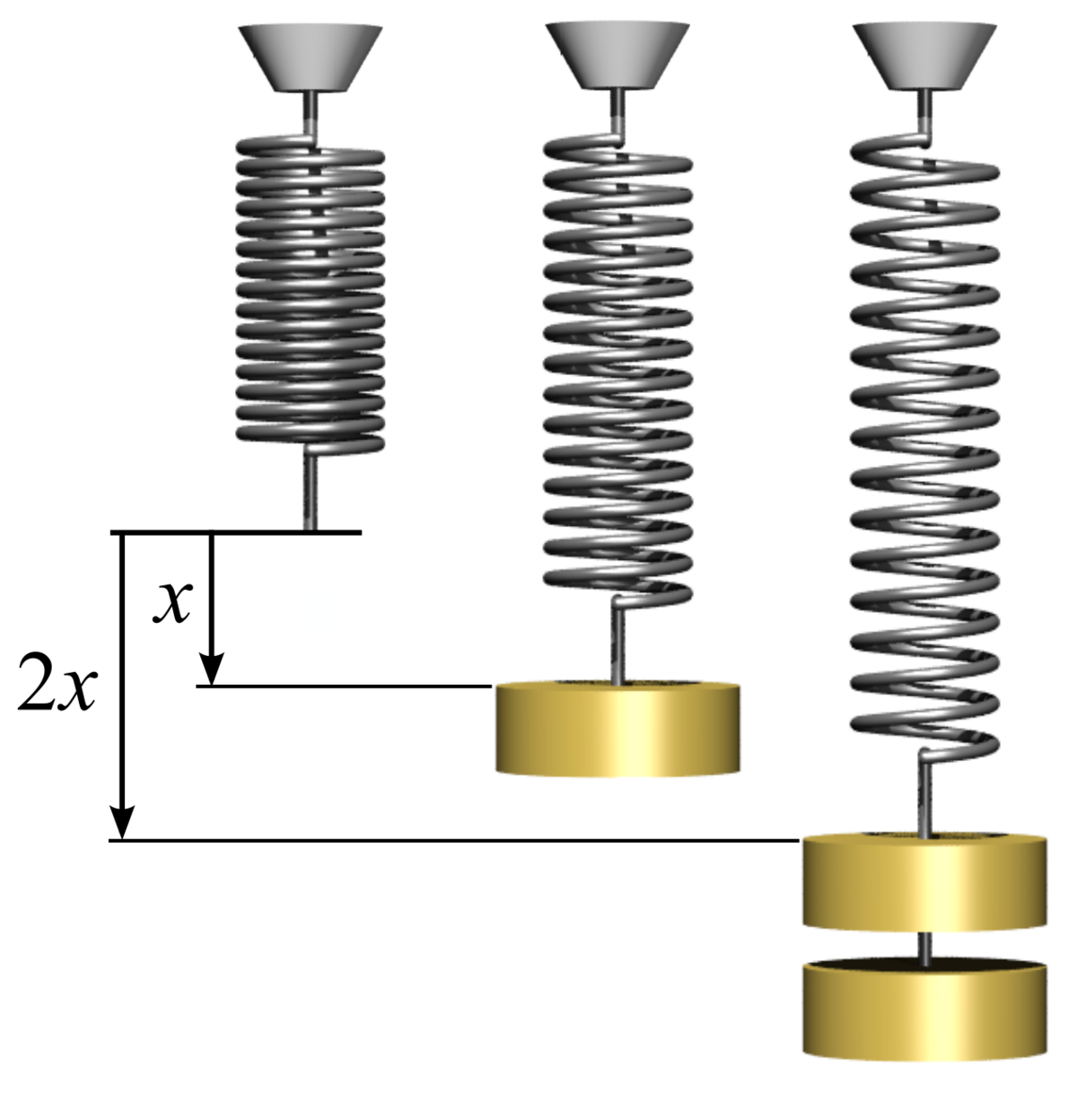
Nehmt euch (falls ihr gerade eine parat habt) eine einfache Feder – nein, nicht von einem Vogel, sondern so ein spiraliges Ding aus Metall. Wenn ihr ein Gewicht an die Feder hängt, wird die Feder um ein Stückchen gedehnt. Hängt ihr ein zweites, genauso schweres Gewicht an die Feder, wird sie noch einmal um den gleichen Betrag gedehnt. Die Dehnung der Feder ist also proportional zur angelegten Kraft (denn die Gewichte üben ja eine Gewichtskraft aus, nach der Formel F=mg).
By Svjo – Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=25398333
Hier noch ein historisches Bild (von dieser schönen Seite) – für uns ist hier erstmal nur Fig.1 interessant, die Feder in der Bildmitte:

Um das als Gleichung hinzuschreiben (und in dieser Serie geht es ja um Gleichungen), müssen wir die Größen, um die es geht, mit Formelzeichen benennen, aber nachdem diese Serie ja schon ein paar teile hat, schreckt euch das ja hoffentlich nicht mehr. Wir nennen die Kraft, die die Feder auf die Gewichte ausübt, F, und die Auslenkung der Feder (also die Länge, um die wir sie gedehnt haben), x. Die Auslenkung x messen wir von der Position aus, wo die Feder im Gleichgewicht ist, wenn kein Gewicht dran hängt. Verdoppeln wir die Auslenkung, dann verdoppelt sich auch die Kraft (weil eine doppelte so große Gewichtskraft die Auslenkung eben verdoppelt). Also sind Kraft und Auslenkung proportional.
Für eine bestimmte Auslenkung (beispielsweise 1mm) bekommen wir eine bestimmte Kraft (beispielsweise 1 Newton), bei 2mm Auslenkung 2 Newton usw. Dieses Verhältnis von Auslenkung und Kraft heißt die “Federkonstante”, meist nimmt man den Buchstaben k dafür. Wir könnten also schreiben
F=k x
wobei k eben die Federkonstante ist (die in unserem Beispiel 1Newton pro Millimeter ist, weil sich bei jeder Dehnung um 1 Millimeter die Kraft um 1 Newton erhöht).
Aber Vorsicht! So ganz korrekt ist die Formel nicht. Wenn wir nämlich die Feder nach unten dehnen, dann wirkt die Kraft, die die Feder ausübt, ja nach oben (und umgekehrt wirkt eine Kraft nach unten, wenn wir die Feder weiter zusammendrücken, falls es eine zusammendrückbare Feder ist). Kraft und Auslenkung gehen also in unterschiedliche Richtungen, deswegen bastelt man besser ein Minuszeichen in die Formel ein:
F=-k x
Diese Beziehung zwischen Kraft und Auslenkung nennt man das Hookesche Gesetz, weil Robert Hooke sie aufgestellt hat. Hooke interessierte sich für Federn, um damit eine Möglichkeit zu finden, genauer gehende Uhren zu bauen (vielleicht habt ihr oben im Bild eine ebene Spiralfeder erkannt, wie man sie in manchen Uhren findet – mehr über Hooke’s Uhrenbau findet ihr unter dem Link oben).
Das Hookesche Gesetz wird auch gern in der Schule im Physikunterricht ausführlich besprochen – es lässt sich im Schulexperiment leicht durch die Schülerinnen* nachbauen, und es ist ein schönes einfaches Beispiel für eine Proportionalität, das man quasi direkt am eigenen Leib erfahren kann (weil man die Federkraft ja auch spüren kann).
*Ja, auch durch die männlichen…
Trotzdem mag das Hookesche Gesetz auf den ersten Blick ziemlich simpel und vor allem uninteressant erscheinen. (Anmerkung: Irgendwo habe ich sogar das Argument gelesen, es sei trivialerweise wahr, weil man die Energie um die Gleichgewichtslage, bei der sie ein Minimum hat, ja in einer mathematischen Reihenentwicklung hinschreiben könnte, deren führender Term eben diese Proportionalität ergibt. Diskutiere ich erstmal nicht weiter, ist aber in meinen Augen ein ziemlich mieses Argument – bei Interesse hinterlasst einen Kommentar.)
Tatsächlich war Hooke aber ziemlich stolz auf dieses Gesetz – die erste Veröffentlichung des Gesetzes von 1660 geschah als Anagramm: ceiiinosssttuv. Auseinandergedröselt: ut tensio, sic vis (wie die Dehnung, so die Kraft); aufgeschlüsselt hat Hooke das erst 1678.
Warum fand Hooke das Gesetz durchaus bemerkenswert? Das hat mehrere Gründe, und die anzugucken, macht das Gesetz vielleicht doch ganz interessant.






Kommentare (10)