Werkstoffe aus dem Computer: Die “Dichtefunktionaltheorie”

Wer neue Werkstoffe entwickeln will (beispielsweise hochfeste Stähle oder Legierungen für Turbinen, die besonders temperaturbeständig sind), ist natürlich auf Experimente angewiesen. Bei uns am Institut beispielsweise werden Test-Legierungen im Ofen zusamengekocht um zu sehen, was passiert und welche Struktur und Festigkeit sie haben.

Denkt man so als theoretische Physikerin darüber nach, fragt man sich, ob das eigentlich so sein muss: Immerhin sind solche Legierungen nichts als ein Haufen Atome, und wie sich Atome und deren Elektronen verhalten, wissen wir eigentlich ziemlich genau, dafür gibt es die berühmte Schrödingergleichung aus der Quantenmechanik. (Keine Sorge, in diesem Artikel brauchen wir die Gleichung selbst gar nicht.) Diese Gleichung beschreibt, wie sich Elektronen verhalten, und prinzipiell sollte es doch möglich sein, die Gleichung für einen Haufen Atome zu lösen. Und letztlich ist eine Legierung ja nichts als ein Haufen Atome und was die tun, wird vor allem durch die Elektronen bestimmt.

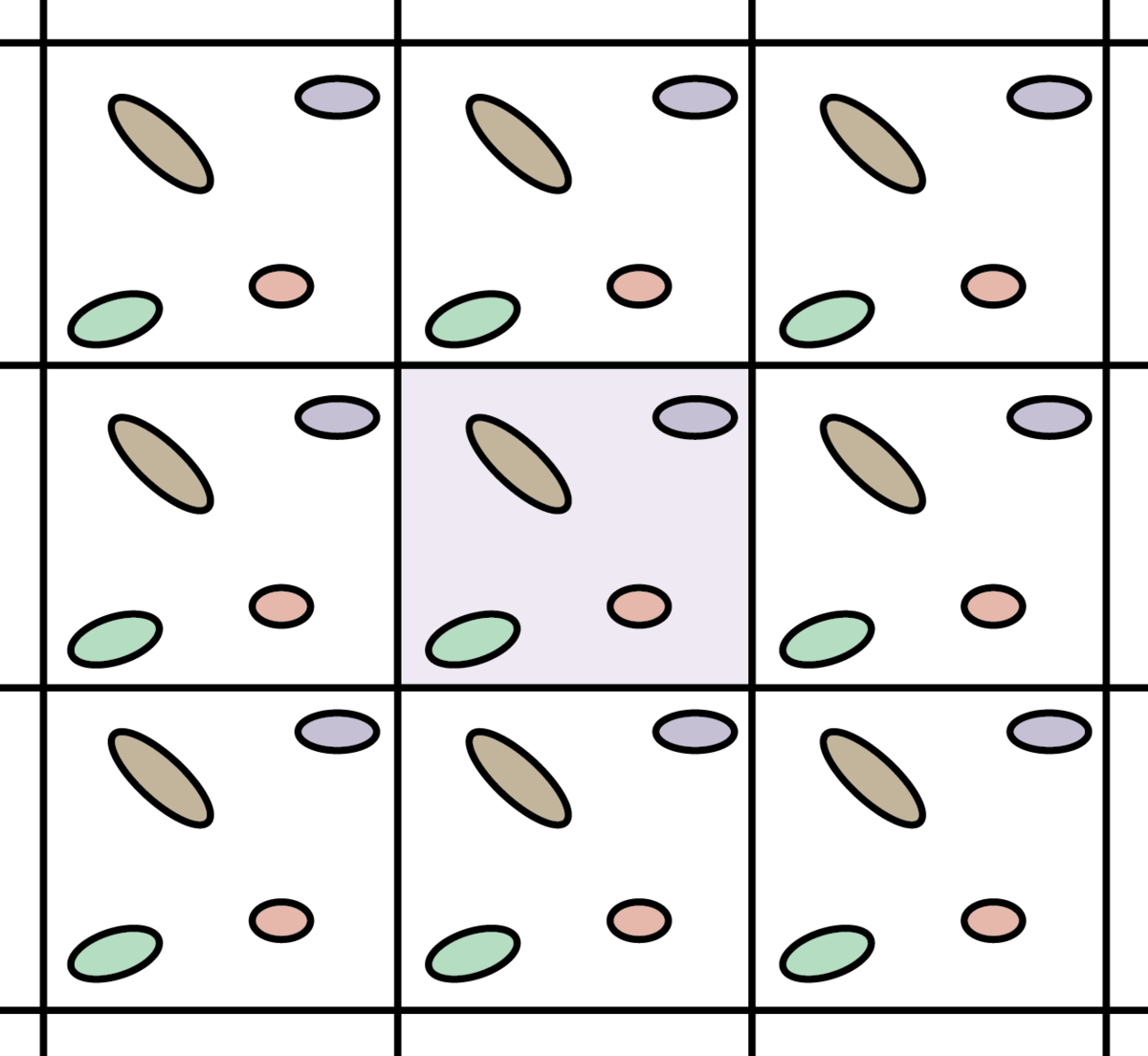
Ein Grund, warum das nicht so einfach ist, ist relativ offensichtlich: Natürlich enthält ein Würfel aus Metall, den man anfassen kann, sehr sehr viele Elektronen, mehr als man berechnen kann. Aber das muss einen prinzipiell nicht zu viel Kopfzerbrechen bereiten, denn man kann ja zum Beispiel ein Stück aus dem Würfel herausschneiden, der dann repräsentativ für den ganzen Würfel steht. So etwa kann man sich das vorstellen:

By Christopher Rowley – Own work, CC BY-SA 4.0, Link

Man tut also so, als bestünde der Materialwürfel aus lauter kleinen, absolut identischen Stücken, ähnlich wie ein Tapetenmuster. Dieser Trick nennt sich “periodische Randbedingungen” und wird in der Physik und auch sonst gern angewendet. Ihr kennt ihn vielleicht auch aus einigen Computerspielen, wo man links auf dem Bildschirm wieder hereinkommt, wenn man rechts rausfliegt. In der Vorlesung illustriere ich das Konzept gern mit diesem Video (von etwa 0:22 bis 1:00). [Da ich keine Ahnung habe, was eine Standard-Youtube-Lizenz ist, insbesondere, wenn die Rechte bei ARD und ZDF liegen, binde ich das jetzt nicht ein…] Funktioniert in der Vorlesung übrigens super, seit ich das Video zeige, beantwortet in der Klausur wirklich jede die Frage nach den Randbedingungen richtig…

Man könnte also einen repräsentativen Ausschnitt aus zum Beispiel nur 1000 Atomen nehmen und den untersuchen.

Auch das ist aber schwierig: Nehmen wir mal 1000 Eisenatome. Die haben zusammen 26000 Elektronen, deren Verhalten wir beschreiben müssen. Das macht man mit einem mathematischen Objekt namens “Wellenfunktion”. Leider ist es bei Elektronen nicht so, dass man, um zwei Elektronen zu beschreiben, einfach zwei Funktionen braucht und für 26000 Elektronen 26000 Funktionen.  Stattdessen braucht man eine einzige gigantische Funktion in einem Raum mit 78000 Dimensionen (26000 mal drei, weil die Welt dreidimensional ist). Warum das so ist und warum eine Funktion in 78000 Dimensionen extrem viel komplizierter ist als 26000 einzelne Funktionen in drei Dimensionen habe ich im Detail hier erklärt.

Als die Quantenmechanik (kurz QM) aufgestellt wurde, hat man deshalb auch schnell gemerkt, dass es praktisch kaum möglich ist, mehr als die allereinfachsten Atome zu berechnen. Wasserstoff ist vergleichsweise simpel (obwohl da eine fiese Differentialgleichung gelöst werden muss), aber alles, was darüber hinausgeht, lässt sich nur noch näherungsweise berechnen. Schon Helium mit seinen zwei Elektronen ist ziemlich knifflig (dazu nutzt man die sogenannte Hartree-Fock-Methode), aber für einen Würfel aus einem Festkörper sieht auch das ziemlich hoffnungslos aus.

Einfacher und hoffnungsvoller wird das ganze, wenn man sich überlegt, dass man sich meist nur für den Grundzustand interessiert, also den Zustand mit der niedrigsten Energie. (In einem typischen Metall bräuchte man Temperaturen von vielen tausend Grad, damit die Elektronen durch die Wärmeenergie ihren Grundzustand verlassen. Und ja, ich vereinfache die Erklärung hier ziemlich gnadenlos, weil ich eigentlich erst mal was über Bandstrukturen in Metallen und solche Sachen schreiben müsste, um das genauer zu erklären. Wenn ihr das ausführlich nachlesen wollt, kann ich euch aber ein gutes Buch empfehlen…)

Für den Grundzustand eines Systems gilt aber ein spezieller Satz der Quantenmechanik, das Hohenberg-Kohn-Theorem. Das sagt folgendes (klingt erst mal kryptisch): Weiß man, in welchem Potential sich die Elektronen bewegen, dann liegt die Dichteverteilung der Elektronen eindeutig fest. Umgekehrt gibt es zu jeder Dichteverteilung auch genau ein Potential, für das diese Verteilung gerade der Grundzustand ist.

Ich drösele das mal ganz in Ruhe auf: Da ist erst mal von einem Potential die Rede. Elektronen sind bekanntlich negativ elektrisch geladen und werden von den positiv geladenen Atomkernen angezogen (sonst gäbe es ja auch keine Atome). Nehmen wir mal an, wir wollen den Grundzustand eines Eisenkristalls (mit 1000 Atomen, periodisch angeordnet) berechnen. Wir können (beispielsweise aus einer Messung mit Röntgenstrahlung) uns überlegen, wie die Atomkerne angeordnet sind und uns dann fragen, wie sich die Elektronen um die Atome verteilen und welche Energie sie haben. (Man kann auch die Positionen der Atomkerne am Ende berechnen und muss sie nicht reinstecken, aber das erkläre ich dann vielleicht später, hier soll es erst mal halbwegs einfach bleiben.)

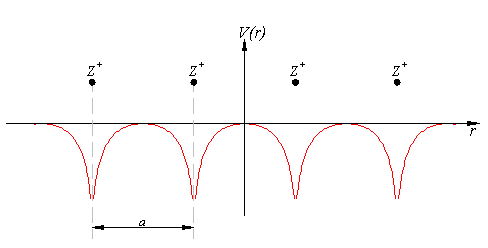
Diese Atomkerne sind elektrisch geladen. Für die Elektronen ist es also energetisch günstig, sich da aufzuhalten, wo die Atomkerne sind, weil sich positive Atomkerne und negative Elektronen ja anziehen. Diese Energie der Elektronen nennt man Potential, und in einer Dimension kann man sich das so vorstellen (Die Atomkerne haben die positive Ladung Z):

 
By LMB, CC BY-SA 3.0, Link

Natürlich ist so eine Anordnung aus lauter positiven Atomkernen nicht stabil, weil sich die Kerne alle abstoßen – stabil wird das Ganze eben durch die Elektronen, die wir in das System bringen. Deren Energie soll nun berechnet werden. Eigentlich müsste man dazu die besagte Funktion in 78000 Dimensionen finden, wenn nicht das Hohenberg-Kohn-Theorem wäre. Das sagt uns nämlich, dass die Energie schon dadurch bestimmt und eindeutig ist, dass wir die Elektronendichte kennen. Wir müssen also für jeden Ort wissen, wie wahrscheinlich es ist, dort ein Elektron zu finden. Statt einer Funktion in 78000 Dimensionen brauchen wir also eine Funktion in drei Dimensionen – einen Wert für jeden Ort. Das klingt ja schon mal besser.

Trotzdem muss man diese Ladungsdichte natürlich irgendwie berechnen. Dazu verwendet man einen zweiten Trick, den sogenannten “Kohn-Sham-Ansatz”. Man berechnet gar nicht wirklich die Ladungsdichte all der vielen Elektronen auf einmal, sondern man bastelt sich ein Hilfsproblem, bei dem man immer nur ein Elektron zur Zeit betrachtet, bei dem aber am Ende dieselbe Ladungsdichte rauskommen soll. Das kleine Problem dabei ist natürlich, dass Elektronen in Wahrheit miteinander wechselwirken, erstens stoßen sie sich elektrisch ab, zweitens können nie zwei Elektronen im selben Zustand sein (das sogenannte Pauli-Prinzip.) Um diese Effekte zu berücksichtigen, bastelt man sie näherungsweise in die zu lösenden Gleichungen ein. (Und je nachdem, wie man diese Näherung macht, ergeben sich unterschiedliche Varianten der Methode, die so schicke Kürzel wie LDA oder GGA tragen.)

Wir lösen also die Schrödinger-Gleichung für 1000 unabhängige Elektronen, aber mit einer kleinen Erweiterung, die die Wechselwirkung halbwegs sinnvoll berücksichtigt. Das Problem dabei wiederum (ja, die Methode ist nicht so ganz einfach) ist, dass die Lösung dieser Gleichung ja von sich selbst abhängt: Die Elektronen wechselwirken ja mit einander. Die Näherungsmethode (die mit den Kürzeln wie LDA oder GGA) erlaubt zwar, diese Wechselwirkung aus der Ladungsdichte abzuschätzen, aber natürlich hängt sie von der Ladungsdichte ab. Um das trotzdem hinzubiegen, geht man so vor:

• Rate eine Lösung für die Ladungsdichte der Elektronen
• Berechne aus der Lösung die Wechselwirkung der Elektronen
• Löse die entstehende Gleichung für die Ladungsdichte der Elektronen
• Vergleiche die berechnete Ladungsdichte mit der vorigen.
• Unterscheiden sich die beiden, gehe zurück zu Schritt 2
• Sind die beiden Lösungen (näherungsweise) gleich, dann haben wir eine Ladungsdichte berechnet, die funktioniert: die Wechselwirkung der Elektronen ist also (im Rahmen der gemachten Näherung) korrekt berücksichtigt.

Man nennt so ein Verfahren “selbstkonsistent” – die genaue Form des Problems hängt von der Lösung ab und man ändert die Lösung so lange, bis alles zusammenpasst.

Die ganze Methode trägt den abgefahrenen Namen “Dichtefunktionaltheorie”. “Dichte” steht für die Dichte der Elektronen, “Funktional”, weil die Energie von der Elektronendichte, also von einer Funktion abhängt (und sowas nennt man in der Mathematik ein Funktional – bekanntestes Beispiel ist ein bestimmtes Integral, dessen Wert von der Funktion abhängt, die man integriert), und “Theorie”, weil es ne Theorie ist. Eigentlich wäre “Methode” vielleicht angemessener, aber DFT hat sich als Begriff durchgesetzt.

Mit diesem schönen Verfahren kann man dann also die Energie unseres Systems aus 1000 Atomen und 26000 Elektronen berechnen. Wobei auch das immer noch ziemlich aufwändig ist – ich rechne meist mit 32 Atomen, manchmal auch mit bis zu 256, und da rechnet ein Supercomputer (ich nutze das HLRN– an dieser Stelle mal gleich ein herzlichen Dankeschön an das HLRN-Team und die Geldgeberinnen, ohne die ich dieses Projekt nicht durchführen könnte) mit z.B. 24*32 Kernen immer noch einige Stunden. Ein ganz schöner Aufwand, um an Ende letztlich nur den Grundzustand eines Systems zu berechnen (bei meinen Rechnungen interessiert mich meist tatsächlich nur eine einzige Zahl, nämlich die Energie).

O.k., wir können also die Energie eines Haufens von Elektronen berechnen (und zwar ziemlich genau). Fragt sich nur, wozu genau das gut sein und wie man damit neue Werkstoffe erfinden soll. Die Antwort liefert (das habt ihr euch sicher schon gedacht) der zweite Teil des Artikels.