Im ersten Teil dieses Artikels habe ich euch erzählt, wie man mit Hilfe der Dichtefunktionaltheorie die Energie einer Ansammlung von Atomen berechnen kann. Nicht erklärt habe ich, warum diese Zahl irgendwie nützlich ist und was man damit anfangen kann. Das tue ich deshalb heute, und zwar an einem Beispiel aus meiner eigenen Forschung.
Als Anwendung schauen wir auf Nickelbasis-Legierungen (manchmal auch “Superlegierungen” genannt – es gibt ein Buch zum Thema, das mit den Worten “Superalloys are indeed super” beginnt…). Solche Legierungen nutzt man beispielsweise in Gasturbinen, weil sie eine hohe Temperaturbeständigkeit haben. Es gibt eine ziemliche Menge an solchen Legierungen. Man kann die grob in zwei Klassen einteilen (aber nur sehr grob): es gibt die absoluten super-duper-Legierungen, die auch bei Temperaturen von 1000 Grad Celsius noch ziemlich fest sind und die man beispielsweise für Turbinenschaufeln nimmt, Nachteil bei denen ist, dass die sich nicht umformen lassen – man gießt sie deshalb gleich in die Form, die man am Ende braucht (da gibt es ziemlich raffinierte Methoden, bei denen man beispielsweise die ganze Schaufel als einen einzigen riesigen Kristall züchtet, aber das ist heute nicht das Thema). Solche Legierungen (naheliegenderweise heißen die “Gusslegierungen”) eignen sich für kleine Bauteile, aber für die größeren Teile in einer Turbine ist Gießen nicht mehr sinnvoll möglich, solche Teile muss man schmieden.
Schmiedlegierungen sind nicht ganz so temperaturbeständig, aber die kommen auch nicht mit dem heißen Gas in der Turbine in Kontakt und bleiben deswegen bei so eher 700 Grad vergleichsweise “kühl”. Dafür kann man sie umformen, also schmieden. Schmieden tut man sie bei Temperaturen von knapp 1000 Grad (alles in Celsius), da sind diese Legierungen nämlich vergleichsweise “weich”. Der Grund dafür ist der, dass sich bei niedrigeren Temperaturen kleine Partikel in der Legierung ausscheiden, die die Legierung fest machen (wie das geht, habe ich zum Beispiel hier und hier mal erklärt). Diese Partikel bestehen aus einer Verbindung aus Nickel und anderen Legierungselementen, berühmt ist beispielsweise die sogenannte gamma-Strich-Phase aus Nickel und Aluminium. In dieser Phase sind Al und Ni ganz regelmäßig angeordnet, das ist energetisch günstig, hat aber den Nachteil, dass die Anordnung eine kleine Entropie besitzt. Bei hohen Temperaturen bestimmt die Entropie das Geschehen und die Teilchen lösen sich auf. (Auch das habe ich mal erklärt.) Die gamma-Strich-Teilchen sind gerade so temperaturstabil, dass sie bei Einsatztemperatur noch da sind, bei der Schmiedetemperatur aber nicht mehr, und nur deswegen ist das Material beim Schmieden überhaupt umformbar. (Die Gusslegierungen sind entsprechend anders, hier sind die härtenden Teilchen auch bei höherer Temperatur noch da, deswegen sind die Legierungen temperaturbeständiger, aber man kann sie genau deswegen auch nicht umformen.)
Also: zum Schmieden möchte man die Teilchen nicht haben, im Einsatz aber schon. Zusätzlich gibt es noch weitere Phasen, beispielsweise die delta-Phase (Nickel und Niob) und die eta-Phase (Nickel und Titan). Diese Phasen machen den Werkstoff nicht wesentlich fester, haben aber die Eigenschaft, dass sie verhindern, dass sich die Struktur des Werkstoffs bei hohen Temperaturen ändert. (Das erkläre ich jetzt nicht im Detail – sie verhindern eine Vergröberung der Körner, also der einzelnen kristallinen Bereiche in der Legierung.) Beim Schmieden möchte man also die gamma-Strich-Phase nicht haben, die delta- oder auch eta-Phase eigentlich aber schon. Diese Phasen müssen also stabiler sein als die gamma-Strich-Phase.
Wenn man Schmiedelegierungen jetzt noch temperaturbeständiger machen will (damit man die Turbine bei höheren Temperaturen betreiben kann), dann muss man die Zusammensetzung so ändern, dass die festigkeitssteigernde Phase auch bei etwas höheren Temperaturen noch stabil ist. (Expertinnenhinweis: In vielen Schmiedelegierungen spielt nicht nur die gamma-Strich, sondern auch die gamma-zwei-Strich-Phase eine wichtige Rolle zur Festigkeitssteigerung, und von anderen Phasen fange ich gar nicht erst an, die sind mir zu kompliziert. Mir geht es hier nur ums Prinzip, damit ihr versteht, was man mit der DFT-Methode machen kann, denn um die ging es eigentlich in diesem Artikel, falls ihr euch noch erinnert…) Das kann man durch Zufügen weiterer Elemente tun – es gibt Elemente, die die Energie der gamma-Strich-Phase weiter absenken (sie also energetisch noch günstiger machen) und die deshalb dazu führen, dass die sich weniger leicht auflöst; genau solche Elemente nutzt man auch in den Gusslegierungen.
Wir kippen also die passenden Elemente in unsere Legierung, aber dann laufen wir natürlich Gefahr, dass wir sie nicht mehr schmieden können, weil bei der Schmiedetemperatur noch zu viel von der härtenden Phase vorhanden ist. Also müssen wir bei höherer Temperatur schmieden. Können wir ja machen, aber dann wiederum bekommen wir ein Problem mit der delta-Phase (oder eta-Phase, je nachdem), denn jetzt könnte sich die ja auflösen, die hat ja auch nur ne begrenzte Temperaturbeständigkeit. Um eine bessere Schmiedelegierung zu bekommen, müssen wir also sowohl die Energie der gamma-Strich als auch die der delta-Phase absenken, damit die gamma-Strich-Phase bei Einsatztemperatur stabil ist, die delta-Phase aber auch bei Schmiedetemperatur. Wir brauchen also passende Legierungselemente, die die Energien der Phasen so beeinflussen, wie wir das wollen.
Man kann natürlich Experimente machen, um den Einfluss von Legierungselementen auf die Phasen zu untersuchen (und das macht man auch). Man kann aber auch einfach (naja, ganz so einfach ist das nicht…) simulieren, und zwar genau mit der DFT-Methode. Wir berechnen also die Energie der delta-Phase mit unterschiedlichen Legierungselementen und knobeln damit heraus, welches Element die delta-Phase stabilisieren kann (also ihre Energie absenkt) und welches das nicht kann. Weil man gerade so schön dabei ist, macht man das auch noch für die eta-Phase, dann hat man einen guten Überblick.
Wir fragen uns also: Welche Energie haben die jeweiligen Phasen im Vergleich zueinander, wenn man diverse Legierungselemente hinzufügt? Dabei muss man etwas aufpassen, man kann natürlich nicht zwei Simulationen vergleichen, in denen ganz unterschiedliche Atome drinstecken. Um das zu sehen, nehmen wir mal den einfachsten Fall: Wir fragen uns erst mal, ob die Delta-Phase (aus Nickel und Niob im Verhältnis 3:1) überhaupt energetisch stabil ist. (Experimentell wissen wir, dass sie das ist, aber wir können ja mal gucken, ob unsere Simulation das auch hergibt.) Wir stellen uns also einen großen Nickelkristall vor (im Idealfall aus unendlich vielen Nickel-Atomen) und schmeißen eine Handvoll Niob-Atome dazu. Die haben jetzt zwei Möglichkeiten: Sie können sich entweder einfach irgendwie im Kristall verteilen (also gelöst sein) oder sie können sich mit Ni-Atomen zur delta-Phase zusammentun, immer ein Nb mit 3 Ni. (Theoretisch könnte es noch andere Dinge tun, beispielsweise sich als reines Nb ausscheiden oder so, aber diese Möglichkeiten interessieren im Moment nicht.) Um zu sehen, was günstiger ist, stellen wir uns vor, wir haben irgendwo schon einen Bereich mit delta-Phase und nehmen jetzt ein weiteres Niob-Atom hinzu. Was möchte dieses Atom lieber tun: Mehr delta-Phase bilden oder sich im Nickel lösen?
Links haben wir den Fall, wo das Nb (grün) in Nickel (vornehm: in der Nickel-Matrix, Atome in blau) gelöst ist, rechts den, wo es in die delta-Phase geht. Wir müssen also die Energie der linken mit der der rechten Seite vergleichen.
Nun wollen wir nicht mit unendlich vielen Atomen rechnen, sondern nur mit endlich vielen. Das lässt sich aber einfach bewerkstelligen: Wir vergleichen den Fall von Nb in einer bestimmten Zahl Ni-Atomen (beispielsweise 15 Ni und ein Nb) mit weniger Nickel-Atomen und dem Nb in der delta-Phase:
Wir vergleichen also die Energie eines Systems aus Ni15Nb mit einem aus 12 Ni-Atomen plus einer Ni3Nb-Zelle. Ist die linke Seite energetisch günstiger, wird das Nb keine delta-Phase bilden wollen, ist die rechte Seite günstiger, bildet sich die delta-Phase. Genau diese Rechnung macht man mit der DFT-Methode. Dazu verwendet man den Trick mit den periodischen Randbedingungen, den ich letztes Mal erklärt habe, damit die simulierten Zellen sich wie Ausschnitte aus einem größeren Material verhalten. (Bevor jemand meckert: natürlich haben wir in Wahrheit in 3D simuliert, übrigens auch mit Ni31Nb, damit das Nb hinreichend “verdünnt” ist.)
Also: diese Rechnung programmieren (in Wahrheit ist die Sache etwas trickreicher, weil das Nb im Nickel die Gitterkonstante ändern kann, also den Abstand der Atome und damit die Größe der Zelle, aber das ignoriere ich heute, dazu kommt vielleich tnoch ein eigener Artikel…), den Superrechner am HLRN in Hannover in Gang treten und wenig später gibt es das Ergebnis: Die delta-Phase ist stabil, die Energie der rechten Seite oben im Bild ist kleiner als die der linken. Wäre sonst ja auch Mist, wir wissen ja experimentell, dass die Phase stabil ist.
Eigentlich wollen wir aber ja wissen, ob andere Legierungselemente die delta-Phase noch stabiler machen. Dazu nutzen wir die gleiche Logik. Nehmen wir zum Beispiel Molybden (in rot). Wir können ein Molybden-Atom in die Nickel-Matrix packen oder in die delta-Phase. Auch hier müssen wir mit der Buchführung aufpassen (man muss immer Konfigurationen vergleichen, die gleich viele Atome von allen Sorten haben):
Wir vergleichen also Ni15Mo + (Ni3Nb)3 auf der einen Seite mit Ni12 + (Ni3Nb)3 Ni3Mo.
Heraus kommt, dass die Energie der rechten Seite kleiner ist, also möchte laut Simulation Mo gern in der delta-Phase sein. (Und dort ein Nb-Atom ersetzen. Man muss auch noch die Möglichkeit berücksichtigen, dass es ein Ni-Atom ersetzt, und wenn man genau hinguckt, gibt es dafür zwei Möglichkeiten, weil die Atome in der delta-Phase ziemlich kompliziert angeordnet sind.)
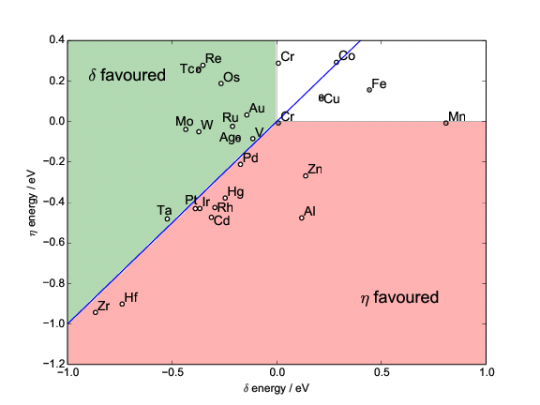
Wir können also daraus schließen, dass Molybden dazu geeignet sein könnte, die delta-Phase zu stabilisieren. Diese Rechnung wiederholen wir jetzt noch für 25 weitere Legierungselemente und auch für die eta-Phase. Dann kommt am Ende ein Diagramm wie dieses heraus:
(Aus Bäker et al.)
Ihr seht für die interessanten Elemente (die meisten Nebengruppenelemente sowie Al), welche Energie man gewinnt oder braucht, um sie in die delta- oder eta-Phase zu bringen. Negative Zahlen heißen, dass die jeweilige Phase günstiger ist; Elemente im weißen Bereich bleiben also lieber im Nickel, die im rosa-farbenen gehen lieber in die eta- die im grünen lieber in die delta-Phase. Die Energieeinheit ist das Elektronenvolt. (Typische chemische Bindungsenergien liegen im Bereich von ein paar eV, Photonen des sichtbaren Lichts haben 1,8-3,5eV.) Dass einige Elemente auch noch graue Punkte haben, hat was mit magnetischen Effekten zu tun, ich ignoriere das mal.
Wer also zum Beispiel die eta-Phase stabilisieren will, könnte das mit Hafnium oder Zirkon tun (die auch die delta-Phase stabilisieren). Natürlich spielen noch andere Effekte hinein, Al bildet ja zum Beispiel die gamma-Strich-Phase, nützt also wenig; Hg beispielsweise ist in Nickel-Legierungen nicht gewollt, weil es irgendwelche komplizierten Versprödungseffekte macht usw. Aber um eine Idee zu bekommen, welche Elemente man sich vielleicht mal näher anschauen sollte, sind diese Simulationen gut geeignet (und genau deswegen mache ich die ja auch bei uns am Institut). Hinterher kann man dann Experimente machen und schauen, ob die Ideen auch stimmen. Experimentell haben wir zum Beispiel Hinweise darauf, dass Cobalt die delta-Phase stabilisiert, aber meine Rechnung zeigt das nicht, da will das Co lieber im Nickel bleiben. Da spielen also vermutlich noch andere Effekte eine Rolle.
Ihr seht also, dass man mit dem Berechnen von Energien in der Materialwissenschaft durchaus einiges anfangen kann.
Bäker, M., Rösler, J., Hentrich, T., & Ackland, G. (2017). Influence of transition group elements on the stability of the δ-and η-phase in nickelbase alloys. Modelling and Simulation in Materials Science and Engineering, 26(1), 015005.









Kommentare (22)