To see a World in a Grain of Sand
And a Heaven in a Wild Flower,
Hold Infinity in the palm of your hand
And Eternity in an hour.
William Blake
In der Allgemeinen Relativitätstheorie hat man es oft mit seltsamen Unendlichkeiten zu tun: In Schwarzen Löchern gibt es Singularitäten (und Ereignishorizonte), und auch unser Universum als Ganzes ist (vermutlich) räumlich und zeitlich unendlich. Damit zu hantieren ist nicht ganz einfach, weil man meist keine unendlich großen Papiere oder Computerbildschirme hat und deswegen nicht alles übersichtlich darstellen kann. Es gibt aber einen Trick, mit dem man sich einen Überblick auch über unendliche Raumzeiten verschaffen kann: Penrose-Diagramme. Die sind leider ein bisschen knifflig zu verstehen (ich gebe zu, ich habe mich damit lange sehr schwer getan), deswegen schauen wir mal ganz in Ruhe, wie das geht (so habe ich’s dann auch verstanden; leider haben diese Erklärungen hier es nicht mehr in mein Buch geschafft, das war eh schon zu dick…)
Wir denken uns erst einmal ein ganz einfaches Universum, das aus der speziellen Relativitätstheorie (SRT). Unser Universum ist statisch, da gab’s keinen Urknall oder sowas, und die Raumzeit ist auch nicht gekrümmt.Unser Universum ist unendlich groß und hat schon immer existiert und das wird es auch für alle Zeit tun.
Wir machen es uns erstmal einfach und denken uns das Universum räumlich eindimensional – es gibt also nur eine Linie, entlang der wir uns bewegen können. Jeden Punkt in unserem Universum können wir dann mit zwei Zahlen kennzeichnen, eine für den Ort (x), eine für die Zeit (t). So etwa könnte man einen Ausschnitt dieses Universums darstellen:

Von Karl Hilpolt – Eigenes Werk, CC BY-SA 4.0, Link
In unserem Universum gelten die Regeln der SRT – Licht bewegt sich immer mit Lichtgeschwindigkeit und nichts ist schneller als das Licht. (Nebenbemerkung: Dass sich nichts schneller als das Licht bewegen kann, kann man mit etwas Geschick direkt aus der Konstanz der Lichtgeschwindigkeit folgern, fragt Isaac, wie das geht…) In unserem Diagramm messen wir Zeiten in Sekunden und Entfernungen in Lichtsekunden (300000km), dann legt das Licht in einer Zeiteinheit auch eine Längeneinheit zurück, so dass Lichtsignale im Diagramm immer unter 45 Grad verlaufen. (Im Bild sind kleine Kegel eingezeichnet, die symbolisieren, dass das Licht sich in unterschiedliche Raumrichtungen ausbreiten kann, aber im Moment lassen wir unser Universum noch räumlich eindimensional.)
So ein Diagramm ist ja ganz nett, hat aber einen Nachteil: Wenn unser Universum unendlich groß ist und unendlich lange existiert hat, dann können wir nicht den ganzen Raum oder die ganze Geschichte des Universums aufzeichnen, es sei denn, wir haben ein unendlich großes Blatt Papier. Gesucht ist deshalb eine Möglichkeit, die gesamte Raumzeit des Universums auf einem endlichen Bereich abzubilden. Das geht natürlich logischerweise nur dann, wenn wir einige Bereiche sehr stark zusammenquetschen.
Dass das prinzipiell aber möglich ist, kennt ihr alle aus dem Zeichenunterricht in der Schule (Diese Analogie habe ich vom backreaction-Blog). Stellt euch unendlich lange Bahnschienen vor (auf einer flachen und unendlich großen Erde). Wenn ihr diese vom Boden aus anschaut, sieht das etwa so aus:

Von Andrzej O – Eigenes Werk, CC BY-SA 3.0, Link
Klar, je weiter die Bahnschienen weg sind, desto enger wird alles zusammengequetscht, aber im Prinzip sind die gesamten Bahnschienen zu sehen (auf der flachen Erde, wohlgemerkt, und natürlich mache ich mir als Theoretikerin keine Gedanken über so Dinge wie Lichtabsorption in der Luft oder sonstiges praktisches Zeugs).
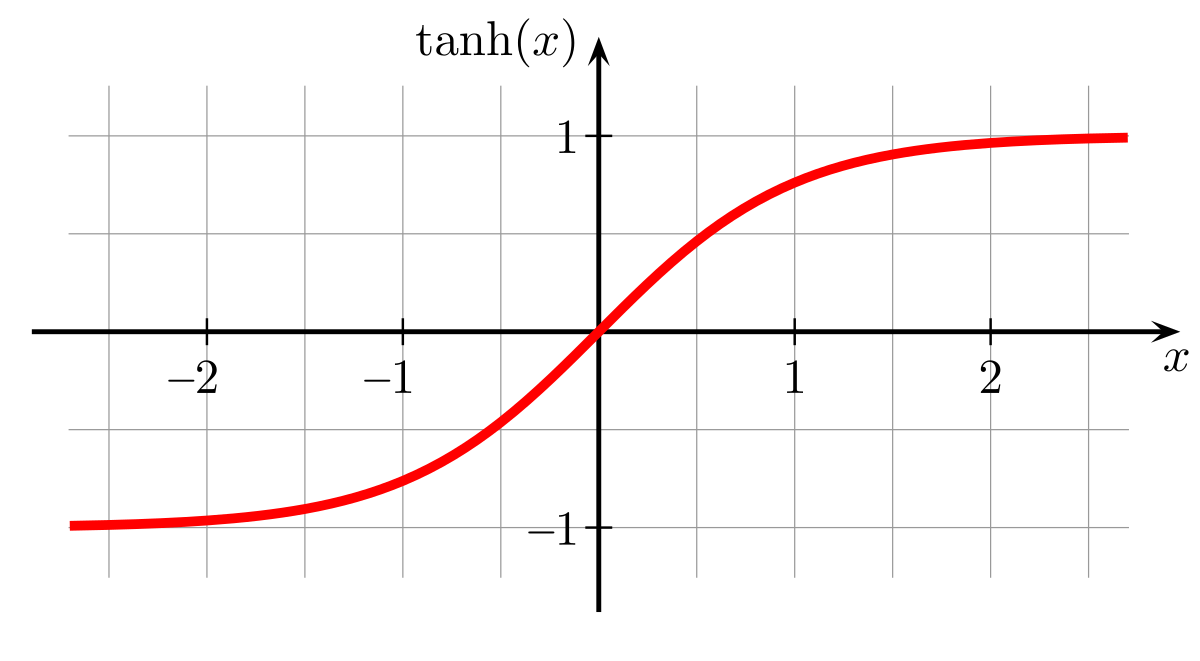
Wir können uns auch einen mathematischen Trick überlegen, wie wir zunächst mal eine Dimension (beispielsweise den Raum x) auf einen endlichen Bereich abbilden können. Dazu können wir beispielsweise diese Funktion (mathematisch ein tangens hyperbolicus) nehmen:
Von Geek3 – Eigenes Werk, CC BY-SA 3.0, Link
Auf der horizontalen Achse sehen wir die tatsächliche Raumkoordinate, auf der vertikalen sehen wir, wie wir diese Raumkoordinate auf einen Wert zwischen -1 und 1 abbilden können. Alles bei Werten größer als 2 oder 3 wird dabei natürlich extrem gestaucht, aber es haben nie zwei unterschiedliche x-Werte exakt denselben Wert unserer neuen Koordinate.
Wir können jetzt also mit diesem Verfahren unser Koordinatensystem auf einen endlichen Bereich abbilden. So würde das aussehen:

Für unsere Zeitkoordinate können wir das genauso machen, dann bekommen wir etwa so ein Bild:

Erinnert ein bisschen an Bilder, die man mit einem Fischaugen-Objektiv macht (dieser Vergleich zu Penrose-Diagrammen wird auch hier gezogen):

By Danielteolijr – Own work, CC BY-SA 4.0, Link
So, damit haben wir also erst einmal einen Trick gefunden, wie wir ein unendlich großes (wenn auch eindimensionales) und unendlich lange existierendes Universum auf einer endlichen Fläche abbilden können. Einiges wird dabei natürlich unendlich stark komprimiert, aber wie wir nachher sehen werden, schadet das nichts, wenn es darum geht, so Dinge wie Schwarze Löcher mit Diagrammen zu erfassen.






Kommentare (4)