Im letzten Teil haben wir uns ja angeguckt, wie man die Raumzeit eines Schwarzen Lochs (SL) in einem Penrose-Diagramm dargestellt, und so schicke Dinge wie (nicht-passierbare) Wurmlöcher und Weiße Zwerge entdeckt. Das Ganze war aber ein bisschen akademisch, weil wir angenommen haben, unser SL wäre statisch und ewig, während sich echte SL erst bilden müssen. (Ein Teil der folgenden Erklärung stammt, leicht modifiziert, aus diesem Link.)
Wir nutzen dazu etwas aus, das schon Newton wusste: Im Inneren einer Schale aus Materie merkt man keine “Schwerkraft” und ist schwerelos. In der ART gilt das immer noch genauso, das heißt die Raumzeit ist hier flach. Wir können uns also vorstellen, wir bauen ein Schwarzes Loch, indem wir mit einem Universum anfangen, bei dem nur ganz weit weg von uns (wo mal das SL entstehen soll) etwas vorhanden ist. Der Einfachheit halber nehmen wir an, dass es sich um Licht handelt. Irgendwer hat bei der Entstehung unseres (hypothetischen) Universums ganz weit weg von uns jede Menge Licht erzeugt, und zwar so, dass dieses Licht genau auf uns zu fliegt. (Licht ist deswegen praktisch, weil die Linien für Licht ja immer unter 45 Grad verlaufen.)
Innerhalb der “Lichtschale” ist das Universum also flach. Weil wir das Licht von außen aufs Zentrum zulaufen lassen (und außen sehr weit weg ist), ist die Energiedichte des Lichts am Anfang sehr klein, wir können also annehmen, dass das Universum am Anfang im wesentlichen überall flach ist. (Ist nur ne Näherung, aber das reicht, weil es am Ende ja nur drauf ankommt, die richtige “Kausalstruktur” hinzubekommen.) So sieht unser Diagramm innerhalb der Lichtschale also jetzt aus:

Achtung: Der Bereich oben (die gelbe Linie) ist nicht die zukünftige Nullunendlichkeit, sondern der Weg des Lichts, das nach Innen stürzt (und nicht vergessen, wir unterdrücken bei diesen Diagrammen ja immer die Winkelkoordinaten; zu jedem Zeitpunkt ist also ein Punkt auf der gelben Linie eine Schale, deren Radius immer kleiner wird).
Als zweiten Schritt stellen wir uns jetzt vor, wir wären außerhalb der Lichtschale. Weit weg von einer Masse kann man sich die Masse in einem Punkt konzentriert vorstellen, damit sieht alles aus wie bei einem gewöhnlichen SL, also so:

Natürlich hat Licht keine Masse, aber Energie, und in die Einstein-Gleichung geht die Energiedichte ein: Licht krümmt die Raumzeit. Um real ein SL aus Licht zu bekommen, bräuchte man schon eine ziemlich helle Lampe, aber wir machen hier ja nur ein Gedankenexperiment, um auf möglichst einfache Weise zu sehen, wie das Penrose-Diagramm eines SL aussehen muss. (Und nachher machen wir das auch für kollabierende Materie wie bei einem Stern.)
Auf wundersame Weise passen die beiden Diagramme ganz prima zusammen, das sieht dann erst mal so aus:

Sieht noch ein bisschen seltsam aus, vor allem, weil der Ereignishorizont einfach plötzlich irgendwo anfängt. Wir können die Linie für den Ereignishorizont aber einfach weiter verlängern – das ändert nichts an der Physik, weil sie unter 45 Grad verläuft und eh nichts schneller als das Licht sein kann. Dann bekommen wir:

Es mag seltsam aussehen, dass es da schon einen Ereignishorizont gibt, bevor sich die rote Linie von links unten und die gelbe Linie für die Lichtschale treffen, aber das ist vollkommen in Ordnung – wie gesagt, nichts ist schneller als das Licht, und wenn dann die Lichtschale erstmal von außen angekommen, dann wird aus der roten Linie, die anfangs eigentlich bloß ein Lichtkegel war, jetzt ein echter Ereignishorizont.
Aber Achtung: die Bezeichnung r=1 gilt nur im oberen Teil, da, wo sich der Ereignishorizont gebildet hat. Falls euch das verwirrt (ging mir auch so), schaut nochmal in Ruhe aufs Diagramm: Da wo die rote Linie losgeht, sind wir bei r=0. Stellt euch vor, ihr sendet hier ein Lichtsignal nach außen. Das bewegt sich entlang der roten Linie von r=0 und trifft dann auf die Lichtschale bei r=1. Genau jetzt bildet sich das SL erst wirklich und unaufhaltsam. Jetzt haben wir also einen “echten” Ereignishorizont und das Licht ist hier eingefroren.
Ihr könntet euch auch fragen, was passiert, wenn ihr ein Lichtsignal in Richtung Zentrum schickt, bevor das SL entstanden ist. Das kreuzt also die rote Linie, fliegt dann nach r=0 und fliegt dann einfach weiter. Im Diagramm wird es dabei reflektiert (das haben wir ja letztes Mal gesehen) und fliegt wieder unter 45 Grad nach außen, schafft es jetzt aber nicht mehr aus dem SL heraus. Es ist also wirklich alles in Ordnung mit der Logik unseres Diagramms, aber man muss aufpassen, weil die 45-Grad-Linie jetzt nicht mehr eine Linie mit konstantem Wert von r ist wie vorher. Ich zeichne mal ein paar Linien ein, dann wird es vielleicht klarer (Achtung: Die Linien habe ich nicht berechnet oder so, sondern nur schematisch eingezeichnet. Der Punkt r=0,5 liegt nicht genau in der Mitte, wenn ich es richtig sehe, sondern etwas weiter links, so ist es zumindest auf dieser Seite hier):

Das ist übrigens auch mal wieder etwas, das in den meisten Erklärungen nicht drinsteht: So ein Ereignishorizont in einem Penrose-Diagramm muss nicht bei einer konstanten r-Koordinate liegen, der Abstand zum Mittelpunkt darf sich ändern.
Unser Diagramm ist soweit sehr schön, aber man kann natürlich argumentieren, dass die Konstruktion mit der Lichtschale ein wenig (o.k., total) künstlich ist. Echte Schwarze Löcher entstehen nicht durch Lichtschalen, sondern durch kollabierende Materie. Wir können aber dagegenhalten, dass das nichts macht, weil das Diagramm ja nur die “kausale Struktur” darstellt. Ob der Ereignishorizont durch zusammenstürzendes Licht oder irgendwas anderes entsteht, sollte egal sei. Wir können das Diagramm also schlicht so umzeichnen, dass wir die Lichtschale durch einen Bereich ersetzen, der mit Materie angefüllt ist und kollabiert (es sieht unten im Bereich so aus, als würde sich der Bereich anfangs ausdehnen, aber das liegt nur daran, dass ja der gesamte Raum bei i- auf einen Punkt zusammengezogen ist):
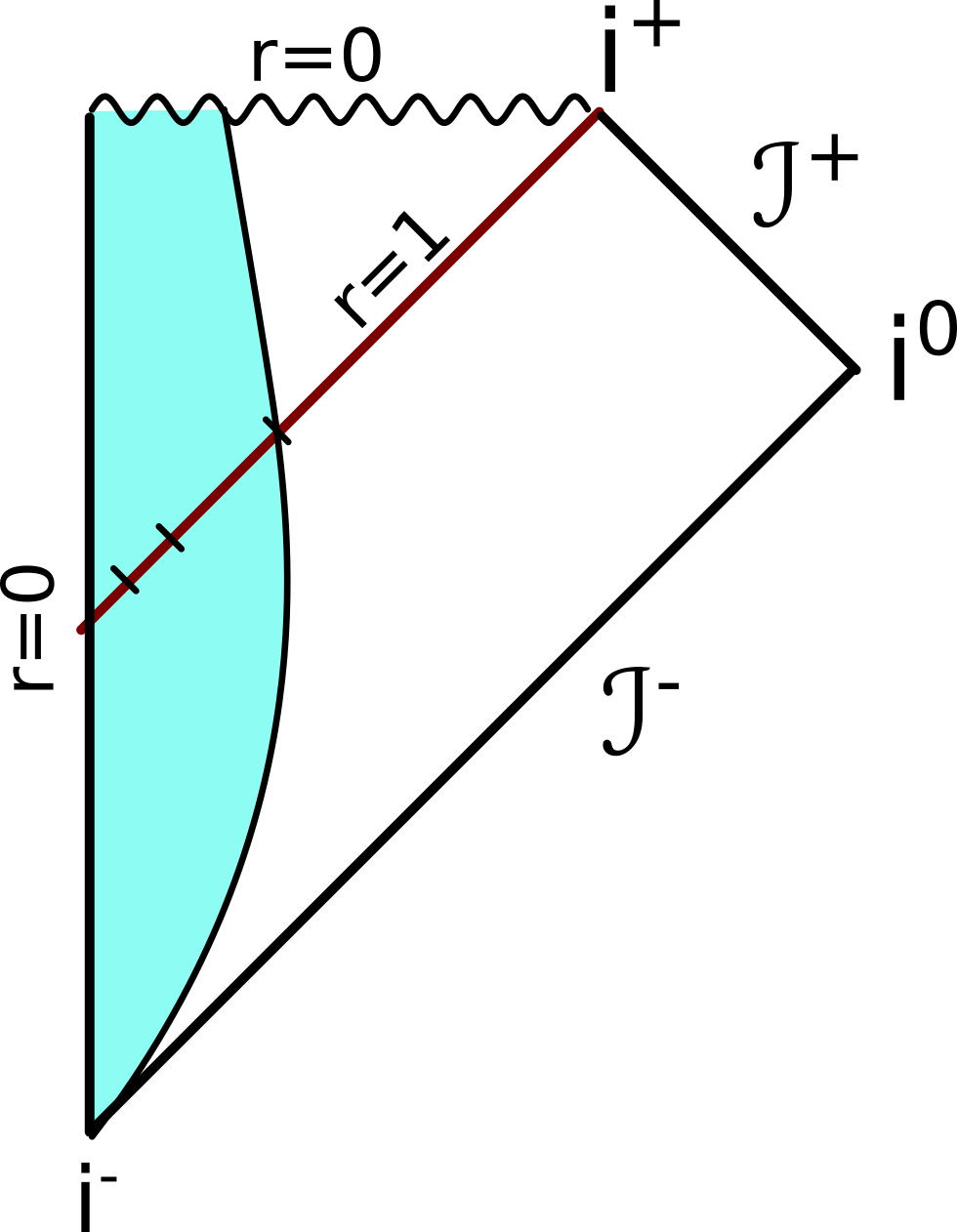
Der Bereich, wo auf dem Ereignishorizont r=1 ist (wo die Linie, die die zusammenstürzende Materie beschreibt, den Ereignishorizont schneidet), liegt jetzt etwas weiter links, das hat aber nur zeichnerische Gründe, sonst sähe das Diagramm zu gequetscht aus.
Wir haben jetzt also das Penrose-Diagramm eines in sich zusammenstürzenden Schwarzen Lochs.
Etwas, das ich wirklich nirgends gefunden habe, ist ein Diagramm dafür, was passiert, wenn weitere Materie in das SL stürzt. Dann nimmt der Schwarzschild-Radius (also die Größe des Ereignishorizonts) ja zu (Dank an Peter Donis von physicsforums, der mir bestätigt hat, dass ich das wohl richtig überlegt habe):
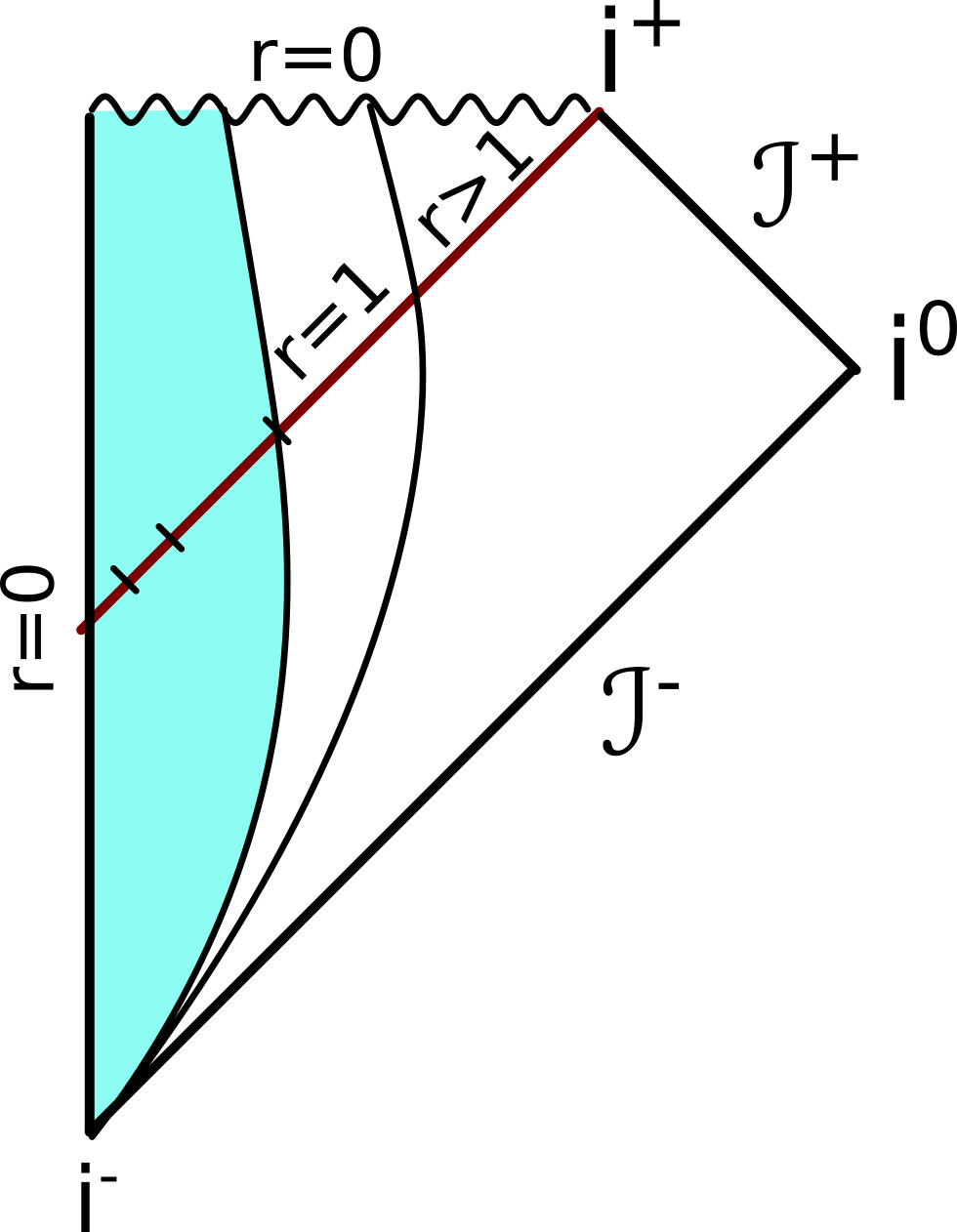
Hier stürzt also noch eine Materieschale (jeder Punkt im Diagramm ist ja eine Kugeloberfläche) in das SL und vergrößert den Ereignishorizont; zwischen dem ersten Punkt bei r=1 und dem bei r>1 darf die Koordinate im Diagramm wieder stetig zunehmen. Der Ereignishorizont wächst, damit würde ein am Ereignishorizont eingefrorener Lichtstrahl ebenfalls “nach Außen” wandern – aber was heißt in einer gekrümmten Raumzeit schon “nach außen”….
Nach der ART allein sind Schwarze Löcher natürlich ewig und können allenfalls größer werden. Aber ihr wisst ja vermutlich (wenn ihr solche abgefahrenen Blogartikel wie diesen hier lest), dass es da (vermutlich) die Hawking-Strahlung gibt, dank derer SL auch wieder schrumpfen können. (Und vergesst bitte die Erklärung mit den “virtuellen Teilchen-Antiteilchen-Paaren am Ereignishorizont”, die ist echt Quatsch. Eine bessere Erklärung findet ihr bei Florian oder in einem guten Buch zur ART, ich wüsste da eins….)
Mir geht’s jetzt aber gar nicht darum, zu erklären, wie die Hawking-Strahlung funktioniert. Nehmen wir einfach an, dass sie funktioniert und dass ein SL Energie und damit Masse verlieren kann und deshalb auch sein Ereignishorizont schrumpft, bis das SL nicht mehr da ist. Wie kann man das passende Penrose-Diagramm dazu basteln?
Der Ereignishorizont muss im Diagramm nach wie vor unter 45 Grad verlaufen. Licht, das dort eingefroren ist, bleibt eingefroren, bis das SL vollständig verschwunden ist. Entlang der Linie für den Ereignishorizont nimmt also der Wert von r wieder ab, je weiter wir im Diagramm nach oben gehen, bis er Null wird. Und dann ist da, wo der Ereignishorizont war, im Diagramm die Null-Koordinate. Insgesamt muss das ganze also so aussehen:
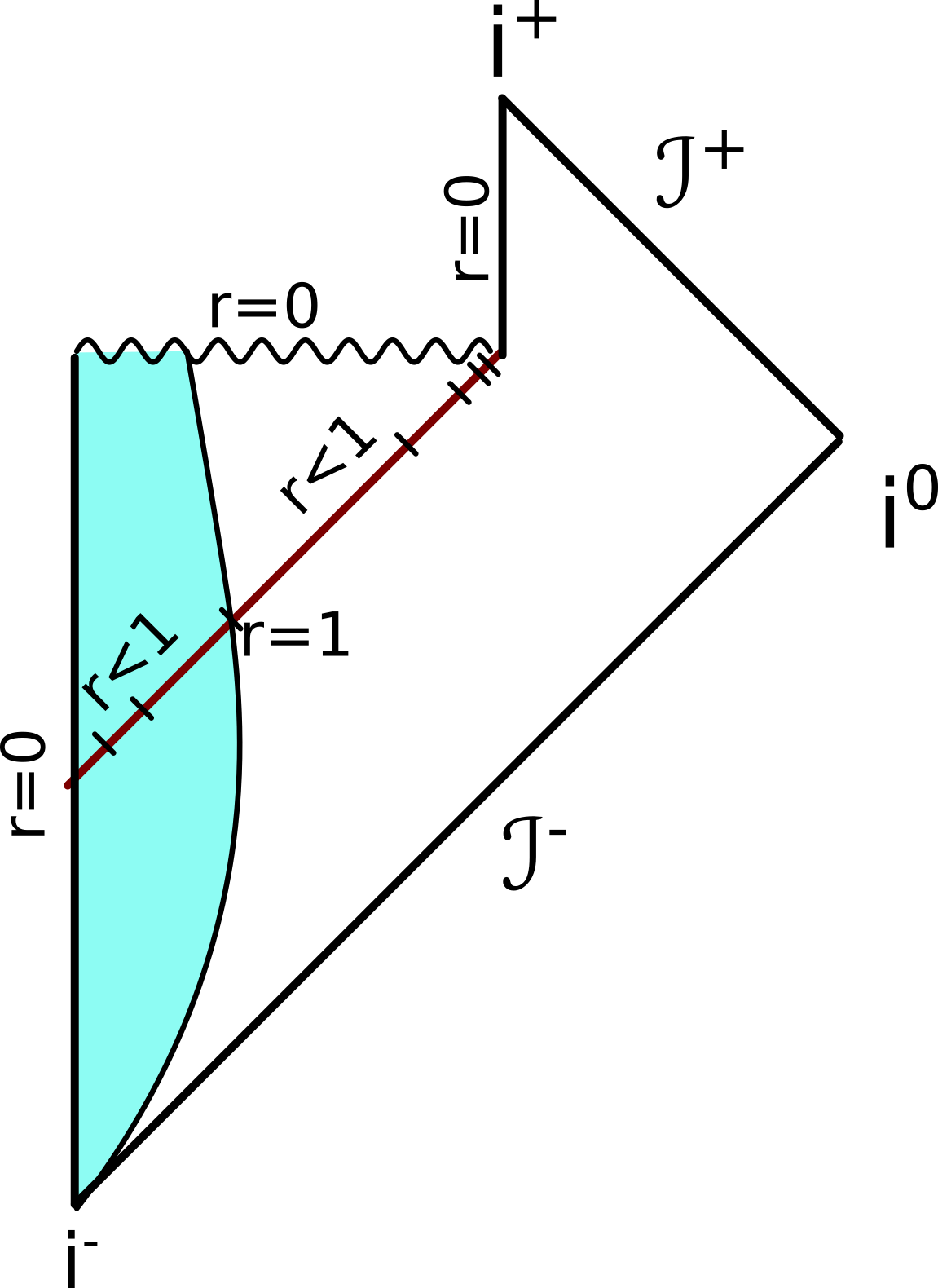
Links haben wir wieder den Bereich, wo sich das SL bildet. Dann hat es für einen Moment den Ereignishorizont bei r=1, aber weil die Hawking-Strahlung seine Masse schrumpfen lässt, nimmt der Wert von r am Ereignishorizont sofort wieder ab. Weil die Strahlung um so schwächer ist, je massereicher das SL ist, habe ich die Striche, die die r-Werte symbolisieren sollen, nach rechts oben hin imer dichter gemacht – das Sl verliert immer schneller an Masse, je leichter es ist, also nimmt auch der Wert von r am Ereignishorizont (warum fällt mir erst jetzt ein, dass ich das klugerweise EH abkürzen könnte? Zu spät.) ab.
Wenn das SL verschwindet, ist der r-Wert des Ereignishorizonts gegen Null gegangen. Im Diagramm ist jetzt also hier eine vertikale Linie mit r=0. Ein Lichtstrahl, der am Horizont eingefroren war, ist jetzt wieder frei und kann ins Universum entkommen, wo er schließlich bei scri+ landet, wie sich das für einen Lichtstrahl im Vakuum gehört. (Falls ihr euch gerade fragt, wie sich die ausgestrahlte Hawking-Strahlung ihrerseits auf das SL auswirkt – das ist das sogenannte (ungelöste) “backreaction”-Problem, das namensgebend für Sabine Hossenfelders Blog ist (den ihr hoffentlich lest).) Auch hier sieht es etwas seltsam aus, weil die Linie für r=0 so seltsame Knicks hat – aber das muss so sein: Alles, was in die Singularität gestürzt ist, ist verschwunden, aber nachdem das SL verdampft ist, haben wir wieder ein vollständiges Universum ohne jeden Ereignishorizont, da muss also im Diagramm irgendwo was seltsames bei r=0 passieren.
So, und damit haben wir Schritt für Schritt entwickelt, wie Penrose-Diagramme funktionieren. (Jetzt verstehe ich selbst es wenigstens auch.) Wirklich praktisch, um zu sehen, welcher Teil der Raumzeit welchen wie erreichen kann. Und war doch gar nicht so schlimm, oder?






Kommentare (11)